在 DNA 测序,蛋白质测序,计算语言学等研究领域,其研究对象可以是一个字符串,也可以是一个短文本,甚至一篇完整的文章。例如:
- 在蛋白质测序领域,其案例形如:Cys-Gly-Leu-Ser-Trp;
- 在 DNA 测序领域,其案例形如:AGCTTCGA;
- 在计算语言学领域,其案例形如:it is rainy today;
在以上的科学领域中,如何对字符串进行研究就显得尤其重要,一种方式是直接对字符和字符串本身进行研究与分析,另一种方式是对字符,单词,句子进行嵌入式的操作,将其映射成欧式空间中的向量,然后再对其进行数据分析和机器学习建模。本篇文章将会从字符与字符串本身出发,分析字符串与字符串之间的性质。
如果需要研究字符串之间的相似性与距离,大致有以下两种方案:
- 基于序列的方法(sequence-based);
- 基于集合的方法(set-based);
顾名思义,可以将字符串看成序列,然后使用序列的相似性或者距离来计算两者之间的性质;也可以将字符串看成集合(或者多重集合),然后使用集合(或者多重集合)的相似性来计算两者之间的性质。
基于集合的方法
n 元语法
n 元语法(n-gram)是自然语言处理中最常见的模型之一,它指的是文本中连续出现的 n 个词语。例如  其 n 元语法分别是:
其 n 元语法分别是:
- 1 元语法(unigram):it, is, rainy, today
- 2 元语法(bigram):it is, is rainy, rainy today
- 3 元语法(trigram):it is rainy, is rainy today
对于一个长度为 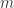 的字符串
的字符串 ![X=X[0,\cdots,m-1]=[X[0],\cdots,X[m-1]]](https://s0.wp.com/latex.php?latex=X%3DX%5B0%2C%5Ccdots%2Cm-1%5D%3D%5BX%5B0%5D%2C%5Ccdots%2CX%5Bm-1%5D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 而言,其 unigram,bigram,trigram,multiset(多重集合)分别是:
而言,其 unigram,bigram,trigram,multiset(多重集合)分别是:
- 1 元语法集合:
![unigram(X)=\{X[i], 0\leq i\leq m-1\};](https://s0.wp.com/latex.php?latex=unigram%28X%29%3D%5C%7BX%5Bi%5D%2C+0%5Cleq+i%5Cleq+m-1%5C%7D%3B&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
- 2 元语法集合:
![bigram(X)=\{X[i]X[i+1], 0\leq i\leq m-2\};](https://s0.wp.com/latex.php?latex=bigram%28X%29%3D%5C%7BX%5Bi%5DX%5Bi%2B1%5D%2C+0%5Cleq+i%5Cleq+m-2%5C%7D%3B&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
- 3 元语法集合:
![trigram(X)=\{X[i]X[i+1]X[i+2], 0\leq i\leq m-3\};](https://s0.wp.com/latex.php?latex=trigram%28X%29%3D%5C%7BX%5Bi%5DX%5Bi%2B1%5DX%5Bi%2B2%5D%2C+0%5Cleq+i%5Cleq+m-3%5C%7D%3B&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
- 1 元语法多重集合:
![multiset(X)=\{X[i]:d[i], 0\leq i\leq m-1\},](https://s0.wp.com/latex.php?latex=multiset%28X%29%3D%5C%7BX%5Bi%5D%3Ad%5Bi%5D%2C+0%5Cleq+i%5Cleq+m-1%5C%7D%2C&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
其中 ![d[i]](https://s0.wp.com/latex.php?latex=d%5Bi%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 表示
表示 ![X[i]](https://s0.wp.com/latex.php?latex=X%5Bi%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 出现的次数。通过 n 元语法,我们可以将一个字符串转换成一个集合,然后通过计算集合之间的相似性来评估字符串的相似性。对于字符串
出现的次数。通过 n 元语法,我们可以将一个字符串转换成一个集合,然后通过计算集合之间的相似性来评估字符串的相似性。对于字符串 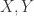 而言,其相似度可以转换为:
而言,其相似度可以转换为:

其中  表示集合的相似度计算函数。
表示集合的相似度计算函数。
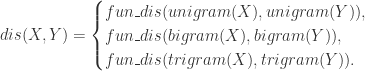
其中 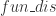 表示集合的距离计算函数。
表示集合的距离计算函数。
集合的相似性或者距离有很多方法可以计算。对于集合 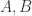 而言,其
而言,其  的选型就包括但不限于以下几种:
的选型就包括但不限于以下几种:
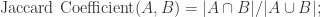




其中, 同时,不仅集合之间可以进行交集,并集的计算,多重集合之间同样可以进行类似的操作,于是上述方法同样可以应用在多重集合上。
同时,不仅集合之间可以进行交集,并集的计算,多重集合之间同样可以进行类似的操作,于是上述方法同样可以应用在多重集合上。
而在字符串距离中,有一个特殊的方法叫做 bag distance,也就是将字符串转换成 unigram 的多重集合,然后计算其距离。令  表示字符串
表示字符串 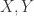 的 unigram 多重集合,然后 bag distance 就可以定义为
的 unigram 多重集合,然后 bag distance 就可以定义为  其中
其中 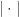 表示多重集合的 SIZE,减法
表示多重集合的 SIZE,减法  表示多重集合的差集。
表示多重集合的差集。
基于序列的方法
最长公共子序列与最长公共子串
在数据结构这门课中,在讲解动态规划的部分,一般都会提到最长公共子序列(Longest Common Subsequence)和最长公共子串(Longest Common Substring)。而子序列和子串其实定义是不一样的。对于序列 ![[x_{0},x_{1},x_{2},\cdots,x_{n}]](https://s0.wp.com/latex.php?latex=%5Bx_%7B0%7D%2Cx_%7B1%7D%2Cx_%7B2%7D%2C%5Ccdots%2Cx_%7Bn%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 而言,其子序列(subsequence)
而言,其子序列(subsequence) ![[x_{n_{1}},\cdots,x_{n_{k}}]](https://s0.wp.com/latex.php?latex=%5Bx_%7Bn_%7B1%7D%7D%2C%5Ccdots%2Cx_%7Bn_%7Bk%7D%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 指的是从原始的序列中通过去除某些元素但不破坏余下元素的相对位置(在前或者在后)而形成的新序列。子串(substring)是相对于一个字符串而言,它是其原始字符串中的完整一段。例如:对于“苹果手机”而言,“苹手”是其子序列,但“苹手”并不是子串。
指的是从原始的序列中通过去除某些元素但不破坏余下元素的相对位置(在前或者在后)而形成的新序列。子串(substring)是相对于一个字符串而言,它是其原始字符串中的完整一段。例如:对于“苹果手机”而言,“苹手”是其子序列,但“苹手”并不是子串。
在这里,如果需要计算两个字符串 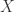 和
和 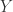 的最长公共子序列的长度和最长公共子串的长度,就需要使用动态规划方面的知识,构建其边界条件和动态转移方程。
的最长公共子序列的长度和最长公共子串的长度,就需要使用动态规划方面的知识,构建其边界条件和动态转移方程。
首先,我们来计算两个字符串 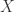 和
和 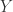 的最长公共子序列。假设
的最长公共子序列。假设 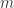 和
和  分别是字符串
分别是字符串 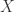 和
和 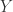 的长度,i.e.
的长度,i.e. ![X=X[0,\cdots,m-1], Y=Y[0,\cdots,n-1].](https://s0.wp.com/latex.php?latex=X%3DX%5B0%2C%5Ccdots%2Cm-1%5D%2C+Y%3DY%5B0%2C%5Ccdots%2Cn-1%5D.&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
令 ![L(m,n)=L(X[0,\cdots,m-1], Y[0,\cdots,n-1])](https://s0.wp.com/latex.php?latex=L%28m%2Cn%29%3DL%28X%5B0%2C%5Ccdots%2Cm-1%5D%2C+Y%5B0%2C%5Ccdots%2Cn-1%5D%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 表示字符串
表示字符串 ![X[0,\cdots,m-1]](https://s0.wp.com/latex.php?latex=X%5B0%2C%5Ccdots%2Cm-1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 和
和 ![Y[0,\cdots,n-1]](https://s0.wp.com/latex.php?latex=Y%5B0%2C%5Ccdots%2Cn-1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 的最长公共子序列的长度。则可以得到其状态转移方程如下:
的最长公共子序列的长度。则可以得到其状态转移方程如下:
![L(m,n)=\begin{cases} L(m-1,n-1)+1, \text{ if } X[m-1] == Y[n-1] \\ \max(L(m-1,n), L(m, n-1)), \text{ else }. \end{cases}](https://s0.wp.com/latex.php?latex=L%28m%2Cn%29%3D%5Cbegin%7Bcases%7D+L%28m-1%2Cn-1%29%2B1%2C+%5Ctext%7B+if+%7D+X%5Bm-1%5D+%3D%3D+Y%5Bn-1%5D+%5C%5C+%5Cmax%28L%28m-1%2Cn%29%2C+L%28m%2C+n-1%29%29%2C+%5Ctext%7B+else+%7D.+%5Cend%7Bcases%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
其边界条件是  返回
返回 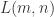 即可表示最长公共子序列的长度。
即可表示最长公共子序列的长度。
例如,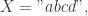
 则有
则有
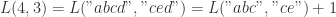

其次,我们来计算两个字符串 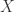 和
和 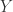 的最长公共子串。假设
的最长公共子串。假设 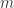 和
和  分别是字符串
分别是字符串 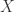 和
和 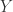 的长度,i.e.
的长度,i.e. ![X=X[0,\cdots,m-1], Y=Y[0,\cdots,n-1].](https://s0.wp.com/latex.php?latex=X%3DX%5B0%2C%5Ccdots%2Cm-1%5D%2C+Y%3DY%5B0%2C%5Ccdots%2Cn-1%5D.&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
令 ![L(m,n)=L(X[0,\cdots,m-1], Y[0,\cdots,n-1])](https://s0.wp.com/latex.php?latex=L%28m%2Cn%29%3DL%28X%5B0%2C%5Ccdots%2Cm-1%5D%2C+Y%5B0%2C%5Ccdots%2Cn-1%5D%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 表示字符串
表示字符串![X[0,\cdots,m-1]](https://s0.wp.com/latex.php?latex=X%5B0%2C%5Ccdots%2Cm-1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 和
和 ![Y[0,\cdots,n-1]](https://s0.wp.com/latex.php?latex=Y%5B0%2C%5Ccdots%2Cn-1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 的最长公共子串的长度。则可以得到其状态转移方程如下:
的最长公共子串的长度。则可以得到其状态转移方程如下:
![L(m,n)=\begin{cases} L(m-1,n-1)+1, \text{ if } X[m-1]==Y[n-1] \\ 0, \text{ else }. \end{cases}](https://s0.wp.com/latex.php?latex=L%28m%2Cn%29%3D%5Cbegin%7Bcases%7D+L%28m-1%2Cn-1%29%2B1%2C+%5Ctext%7B+if+%7D+X%5Bm-1%5D%3D%3DY%5Bn-1%5D+%5C%5C+0%2C+%5Ctext%7B+else+%7D.+%5Cend%7Bcases%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
其边界条件是  返回:
返回: 即可表示最长公共子串的长度。
即可表示最长公共子串的长度。
例如: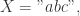
 则有最长公共子串的长度是
则有最长公共子串的长度是 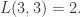
Jaro 和 Jaro-Winkler 相似度
首先,我们来定义两个字符串之间的 Jaro 相似度。对于两个字符串 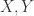 而言,如果两个字符
而言,如果两个字符 ![X[i], Y[j]](https://s0.wp.com/latex.php?latex=X%5Bi%5D%2C+Y%5Bj%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 满足以下两个条件:
满足以下两个条件:
![X[i]=Y[j];](https://s0.wp.com/latex.php?latex=X%5Bi%5D%3DY%5Bj%5D%3B&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
![|i-j|\leq [\max(|X|,|Y|)/2]-1;](https://s0.wp.com/latex.php?latex=%7Ci-j%7C%5Cleq+%5B%5Cmax%28%7CX%7C%2C%7CY%7C%29%2F2%5D-1%3B&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
则 ![X[i],Y[j]](https://s0.wp.com/latex.php?latex=X%5Bi%5D%2CY%5Bj%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 被称为匹配(matching),其中
被称为匹配(matching),其中 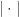 表示 string 的长度,
表示 string 的长度,![[\cdot]](https://s0.wp.com/latex.php?latex=%5B%5Ccdot%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 表示高斯取整函数。在此定义下计算出
表示高斯取整函数。在此定义下计算出 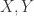 的匹配字符为
的匹配字符为  从定义可以得到
从定义可以得到  的长度是一样的,记为
的长度是一样的,记为 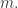 令
令 ![t=[\#\{0\leq i\leq m-1:X'[i]\neq Y'[i]\}/2]](https://s0.wp.com/latex.php?latex=t%3D%5B%5C%23%5C%7B0%5Cleq+i%5Cleq+m-1%3AX%27%5Bi%5D%5Cneq+Y%27%5Bi%5D%5C%7D%2F2%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 称为 transposition。于是,Jaro 相似度就可以定义为:
称为 transposition。于是,Jaro 相似度就可以定义为:

例如,
 可以得到
可以得到 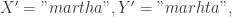 于是
于是  因此,Jaro 相似度是
因此,Jaro 相似度是

 可以得到
可以得到  于是
于是  因此,Jaro 相似度是
因此,Jaro 相似度是

 可以得到
可以得到  于是
于是  因此,Jaro 相似度是
因此,Jaro 相似度是

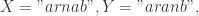 可以得到
可以得到  于是
于是  因此,Jaro 相似度是
因此,Jaro 相似度是

其次,我们来定义两个字符串之间的 Jaro-Winkler 相似度。对于字符串 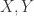 而言,其 Jaro-Winlker 相似度定义为:
而言,其 Jaro-Winlker 相似度定义为:


其中 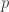 表示系数(默认是 0.1,可以调整),
表示系数(默认是 0.1,可以调整),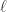 表示
表示  的最长前缀子串的 SIZE,并且不超过 4。
的最长前缀子串的 SIZE,并且不超过 4。
例如: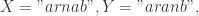 可以得到
可以得到  因此,Jaro-Winkler 相似度为
因此,Jaro-Winkler 相似度为 
Levenshtein 距离
Levenshtein 距离是编辑距离的一种形式,所谓编辑距离,指的是在两个字符串之间,由一个转成另外一个所需要的最少编辑次数。在这里的编辑操作包括:
- 更换:将一个字符更换为另一个字符;
- 删除:删除一个字符;
- 插入:插入一个字符;
对于字符串 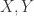 而言,
而言,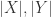 分别表示字符串
分别表示字符串 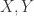 的长度。则可以用动态规划的思想来计算 Levenshtein 距离。用
的长度。则可以用动态规划的思想来计算 Levenshtein 距离。用  表示
表示 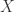 的前
的前 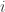 个字符和
个字符和 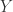 的前
的前 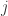 个字符的 Levenshtein 距离,
个字符的 Levenshtein 距离,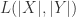 表示两个字符串的 Levenshtein 距离。
表示两个字符串的 Levenshtein 距离。
![Lev(i,j)=\begin{cases} j, \text{ if } i=0,\\ i, \text{ else if } j=0,\\ \min\begin{cases}Lev(i-1,j)+1,\\ Lev(i,j-1)+1,\\ Lev(i-1,j-1)+1_{X[i-1]\neq Y[j-1]} \end{cases}\text{ otherwise }.\end{cases}](https://s0.wp.com/latex.php?latex=Lev%28i%2Cj%29%3D%5Cbegin%7Bcases%7D+j%2C+%5Ctext%7B+if+%7D+i%3D0%2C%5C%5C+i%2C+%5Ctext%7B+else+if+%7D+j%3D0%2C%5C%5C+%5Cmin%5Cbegin%7Bcases%7DLev%28i-1%2Cj%29%2B1%2C%5C%5C+Lev%28i%2Cj-1%29%2B1%2C%5C%5C+Lev%28i-1%2Cj-1%29%2B1_%7BX%5Bi-1%5D%5Cneq+Y%5Bj-1%5D%7D+%5Cend%7Bcases%7D%5Ctext%7B+otherwise+%7D.%5Cend%7Bcases%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
其中 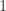 表示指示函数,
表示指示函数,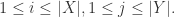
例如:kitten -> sitting 的 Levenshtein 距离就是 3。因为
- kitten -> sitten:替换 k -> s;
- sitten -> sittin:替换 e -> i;
- sittin -> sitting:增加 g.
距离与相似度的转换
对于相似度 sim 和距离 dist 而言,只要找到某个递减函数就可以将其互相转换。
![f:[0,+\infty)\rightarrow [-1,1]](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C%2B%5Cinfty%29%5Crightarrow+%5B-1%2C1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 是将距离转换成相似度的函数,则可以表示为
是将距离转换成相似度的函数,则可以表示为  其中,
其中,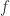 是严格递减函数,值域属于
是严格递减函数,值域属于 ![[-1,1],](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D%2C&bg=ffffff&fg=2b2b2b&s=0&c=20201002)

![g:[-1,1]\rightarrow [0,+\infty)](https://s0.wp.com/latex.php?latex=g%3A%5B-1%2C1%5D%5Crightarrow+%5B0%2C%2B%5Cinfty%29&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 是将相似度转换为距离的函数,则可以表示为
是将相似度转换为距离的函数,则可以表示为  其中,
其中,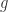 是严格递减函数,值域属于
是严格递减函数,值域属于 

例如:
- Levenshtein 相似度就可以用函数
 来转换;
来转换; - 基于最长公共子串/最长公共子序列的相似度既可以使用函数
 也可以使用函数
也可以使用函数  来计算。
来计算。
开源工具 py_stringmatching
如果需要计算两个字符串的相似性,可以直接使用开源工具 py_stringmatching。通过 py_stringmatching 的官网可以看到,其主要功能分成两个部分,第一部分是 Tokenizers 的介绍,第二部分是各种相似度的计算。
Tokenizer
在第一部分 Tokenizers 中,本质上就是将一个字符串切分成一个序列。其主要的切分函数分成五种,分别是:
- Alphabetic Tokenizer:返回最长连续的英文序列;
- Alphanumeric Tokenizer:返回最长连续的英文/数字序列;
- Delimiter Tokenizer:根据某个指定的字符串来进行切分;
- Qgram Tokenizer:基于 Q 元语法的切分;
- Whitespace Tokenizer:基于空格的切分。
从以上的切分方式来看,py_stringmatching 更适用于英文,因为中文需要使用专门的切词工具。这里的 return_set=True 指的是返回 set(去除重复的元素)。
首先来看 Alphabetic Tokenize 的案例:
from py_stringmatching import AlphabeticTokenizer
al_tok = AlphabeticTokenizer()
print(al_tok.tokenize('algebra88analysis, geometry#geometry.'))
# 输出:['algebra', 'analysis', 'geometry', 'geometry']
al_tok = AlphabeticTokenizer(return_set=True)
print(al_tok.tokenize('algebra88analysis, geometry#geometry.'))
# 输出:['algebra', 'analysis', 'geometry']
其次来看 Alphanumeric 的案例:
from py_stringmatching import AlphanumericTokenizer
alnum_tok = AlphanumericTokenizer()
print(alnum_tok.tokenize('algebra9,(analysis), geometry#.(geometry).88'))
# 输出:['algebra9', 'analysis', 'geometry', 'geometry', '88']
alnum_tok = AlphanumericTokenizer(return_set=True)
print(alnum_tok.tokenize('algebra9,(analysis), geometry#.(geometry).88'))
# 输出:['algebra9', 'analysis', 'geometry', '88']
然后看 Delimiter Tokenizer 的案例:
from py_stringmatching import DelimiterTokenizer
delim_tok = DelimiterTokenizer()
print(delim_tok.tokenize('algebra analysis geometry geometry'))
# 输出:['algebra', 'analysis', 'geometry', 'geometry']
delim_tok = DelimiterTokenizer(delim_set={'$ #$'})
print(delim_tok.tokenize('algebra$ #$analysis'))
# 输出:['algebra', 'analysis']
delim_tok = DelimiterTokenizer(delim_set={',', '.'})
print(delim_tok.tokenize('algebra,analysis,geometry.geometry'))
# 输出:['algebra', 'analysis', 'geometry', 'geometry']
delim_tok = DelimiterTokenizer(delim_set={',', '.'}, return_set=True)
print(delim_tok.tokenize('algebra,analysis,geometry.geometry'))
# 输出:['algebra', 'analysis', 'geometry']
再次来看 Q 元语法的案例:QgramTokenize 的参数包括:
- qval = 2:q 元数组;
- padding = True:是否需要加上前后缀;
- prefix_pad =‘#’:前缀;
- suffix_pad = ‘$’:后缀;
- return_set = True:是否去重
from py_stringmatching import QgramTokenizer
qgram_tok = QgramTokenizer()
print(qgram_tok.tokenize('algebra'))
# 输出:['#a', 'al', 'lg', 'ge', 'eb', 'br', 'ra', 'a$']
qgram_tok = QgramTokenizer(qval=3)
print(qgram_tok.tokenize('algebra'))
# 输出:['##a', '#al', 'alg', 'lge', 'geb', 'ebr', 'bra', 'ra$', 'a$$']
qgram_tok = QgramTokenizer(padding=False)
print(qgram_tok.tokenize('algebra'))
# 输出:['al', 'lg', 'ge', 'eb', 'br', 'ra']
qgram_tok = QgramTokenizer(prefix_pad='^', suffix_pad='!')
print(qgram_tok.tokenize('algebra'))
# 输出:['^a', 'al', 'lg', 'ge', 'eb', 'br', 'ra', 'a!']
最后来看 Whitespace Tokenize 的案例:
from py_stringmatching import WhitespaceTokenizer
ws_tok = WhitespaceTokenizer()
print(ws_tok.tokenize('algebra analysis geometry geometry topology'))
# 输出:['algebra', 'analysis', 'geometry', 'geometry', 'topology']
print(ws_tok.tokenize('algebra analysis geometry geometry topology'))
# 输出:['algebra', 'analysis', 'geometry', 'geometry', 'topology']
ws_tok = WhitespaceTokenizer(return_set=True)
print(ws_tok.tokenize('algebra analysis geometry geometry topology'))
# 输出:['algebra', 'analysis', 'geometry', 'topology']
Similarity Measures
下面来介绍开源工具 py_stringmatching 的常见相似度函数。
Bag Distance,Levenshtein 函数的使用:
from py_stringmatching import BagDistance
bd = BagDistance()
print(bd.get_raw_score('algebra', 'algebraic'))
# 输出:2
print(bd.get_sim_score('algebra', 'algebraic'))
# 输出:0.7778
from py_stringmatching import Levenshtein
lev = Levenshtein()
print(lev.get_raw_score('algebra', 'algebraic'))
# 输出:2
print(lev.get_sim_score('algebra', 'algebraic'))
# 输出:0.7778
其中 bag,Levenshtein 相似度的定义是  其中
其中 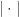 表示字符串的长度,
表示字符串的长度, 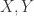 表示字符串。
表示字符串。
Cosine,Dice,Jaccard,OverlapCoefficient,TverskyIndex 函数的使用:
- 这些函数的输入都是 set 或者 list;
- 如果是需要比较字符串,则可以使用 Tokenizer 函数将其切分或者转换,例如 1 gram;
- 这些函数的 get_raw_score 与 get_sim_score 是一样的,因为都是相似度函数。
from py_stringmatching import Cosine, Dice, Jaccard, OverlapCoefficient
cos = Cosine()
print(cos.get_raw_score(['algebra'], ['algebra', 'analysis']))
# 输出:0.7071
dice = Dice()
print(dice.get_raw_score(['algebra'], ['algebra', 'analysis']))
# 输出:0.6667
jaccard = Jaccard()
print(jaccard.get_raw_score(['algebra'], ['algebra', 'analysis']))
# 输出:0.5
overlap = OverlapCoefficient()
print(overlap.get_raw_score(['algebra'], ['algebra', 'analysis']))
# 输出:1.0
tversky = TverskyIndex()
print(tversky.get_raw_score(['algebra'], ['algebra', 'analysis']))
# 输出:0.6667
Jaro,Jaro Winkler 函数的使用:
- 这两个函数的输入都是 string;
- 这两个函数的 get_raw_score 与 get_sim_score 是一样的;
from py_stringmatching import Jaro
jaro = Jaro()
print(jaro.get_raw_score('algebra', 'algebraic'))
print(jaro.get_sim_score('algebra', 'algebraic'))
# 输出:0.9259
from py_stringmatching import JaroWinkler
jw = JaroWinkler()
print(jw.get_raw_score('algebra', 'algebraic'))
print(jw.get_sim_score('algebra', 'algebraic'))
# 输出:0.9556
Hamming 距离的使用:
- 只能适用于长度一致的字符串;
- 相似度的计算是通过
 得到的;
得到的;
from py_stringmatching import HammingDistance
hm = HammingDistance()
print(hm.get_raw_score('algebra', 'algebri'))
# 输出:1
print(hm.get_sim_score('algebra', 'algebri'))
# 输出:0.8571
开源工具 FuzzyWuzzy
FuzzyWuzzy 是一个计算 STRING 相似度的开源工具库,其值域是 ![[0,100].](https://s0.wp.com/latex.php?latex=%5B0%2C100%5D.&bg=ffffff&fg=2b2b2b&s=0&c=20201002) 如果需要计算相似度,直接除以 100 即可。
如果需要计算相似度,直接除以 100 即可。
from fuzzywuzzy import fuzz
print(fuzz.partial_ratio('algebra is interesting', 'algebraic is good'))
# 输出:65
print(fuzz.partial_token_sort_ratio('algebra is interesting', 'algebraic is good'))
# 输出:59
print(fuzz.partial_token_set_ratio('algebra is interesting', 'algebraic is good'))
# 输出:100
print(fuzz.token_sort_ratio('algebra is interesting', 'algebraic is good'))
# 输出:62
print(fuzz.token_set_ratio('algebra is interesting', 'algebraic is good'))
# 输出:62
开源工具 python-Levenshtein
Levenshtein 距离也可以使用开源工具 python-Levenshtein 来计算,形如:
from Levenshtein import distance
print(distance('algebra', 'algebraic'))
# 输出 2
参考资料:
- 最长公共子串:https://www.geeksforgeeks.org/longest-common-substring-dp-29/
- 最长公共子序列:https://www.geeksforgeeks.org/longest-common-subsequence-dp-4/
- Jaro 与 Jaro-Winkler 相似度:https://www.geeksforgeeks.org/jaro-and-jaro-winkler-similarity/
- Levenshtein 距离:https://en.wikipedia.org/wiki/Levenshtein_distance
- n 元语法:https://zh.wikipedia.org/wiki/N%E5%85%83%E8%AF%AD%E6%B3%95
- 开源工具 py_stringmatching:https://anhaidgroup.github.io/py_stringmatching/v0.4.2/index.html
- 开源工具 FuzzyWuzzy:https://github.com/seatgeek/fuzzywuzzy
- 开源工具 python-Levenshtein:https://github.com/ztane/python-Levenshtein/
- Cui, Yi, et al. “Finding email correspondents in online social networks.” World Wide Web 16.2 (2013): 195-218.
- Rieck, Konrad, and Christian Wressnegger. “Harry: A tool for measuring string similarity.” The Journal of Machine Learning Research 17.1 (2016): 258-262.




















































![£¨Í¼±í£©[Éç»á]2020Äê½Ú¼ÙÈշżٰ²ÅŹ«²¼](https://zr9558.files.wordpress.com/2020/05/2020e5b9b4e4b8ade59bbde88a82e58187e697a5e5ae89e68e92.jpg)