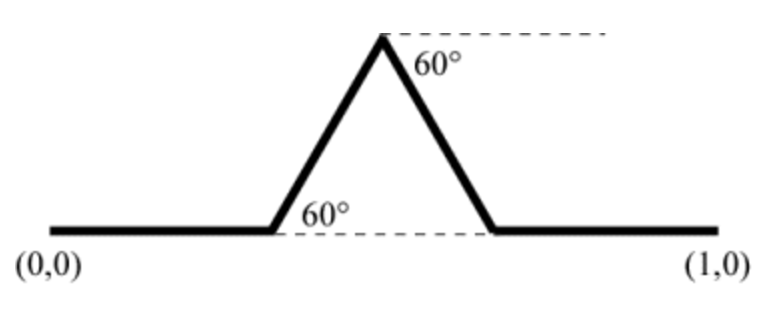
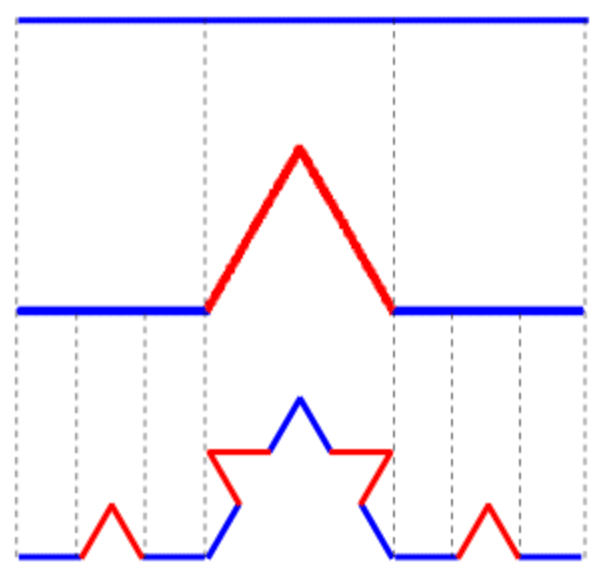
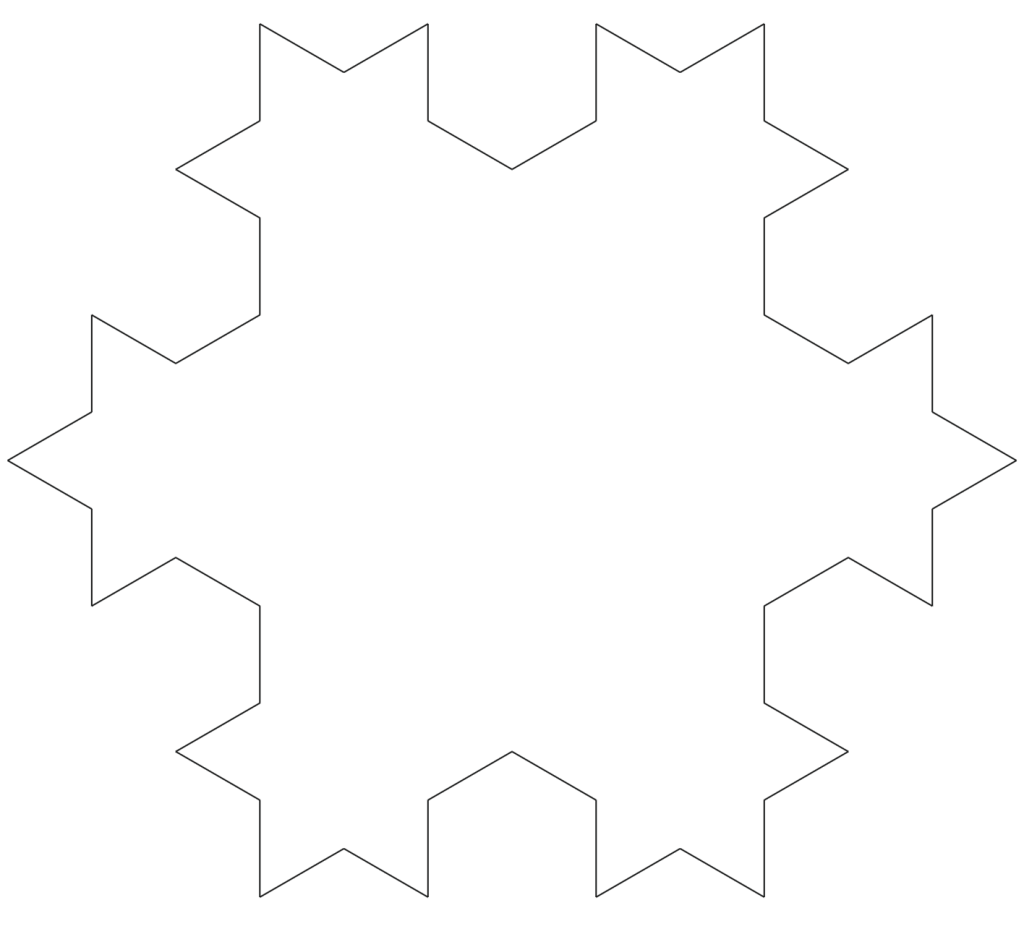
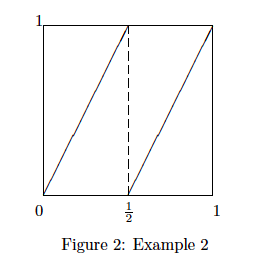
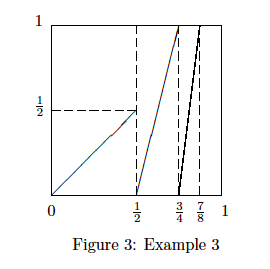
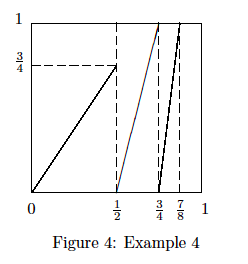
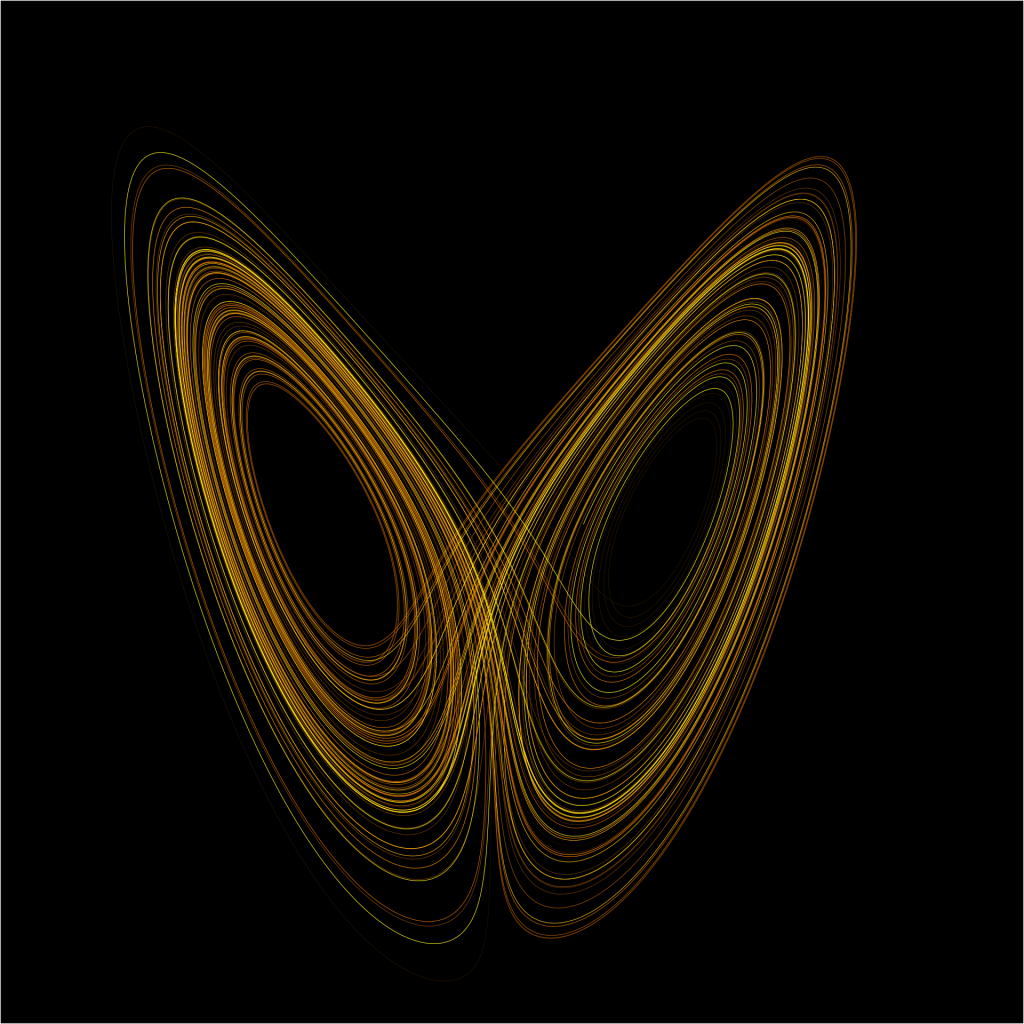我们用科普的角度来聊聊“一维动力系统”（One-Dimensional Dynamics）。
想象一下，你有一个非常简单的规则，这个规则告诉你：根据一个点当前的位置，如何确定它下一刻的位置。然后你不断地、一遍又一遍地应用这个规则。研究这个点在“时间”（可以理解为迭代次数）推进下如何运动、最终会去哪里、系统整体会表现出什么性质的学问，就是动力系统理论。
当这个点只能在一条线上移动时（比如一条无限长的数轴，或者一个首尾相接的圆圈），我们研究的系统就叫做一维动力系统。
为什么研究“一维”？
- 简单但深刻： 一维是维度最低的情况，规则相对简单，更容易分析和理解。但别小看它，即使是最简单的一维规则，也能产生极其复杂和令人惊讶的行为（比如混沌）。
- 基础性： 理解了一维系统的行为，是理解更高维（二维、三维甚至无穷维）更复杂系统的基础。很多高维系统中的核心思想和现象（如混沌、分形、吸引子）都能在一维模型中找到原型或被深刻理解。
- 应用广泛： 虽然模型简单，但一维动力系统可以用来描述很多实际现象的简化模型，比如：
（1）种群增长： 今年昆虫的数量决定了明年的大致数量（考虑环境承载力的限制）。
（2）简单物理过程： 单摆的近似运动（在小角度时）。
（3）经济模型： 简单的市场供需关系演化。
（4）信号处理： 某些反馈机制。
一维动力系统的核心要素：
- “舞台”： 点运动的空间。主要分两类：
- 区间： 比如一条线段
[0, 1]。点不能跑出这个范围。 - 圆周： 像一个环
S¹。点跑出“右边界”会从“左边界”回来（反之亦然）。想象一个圆盘边缘的点。
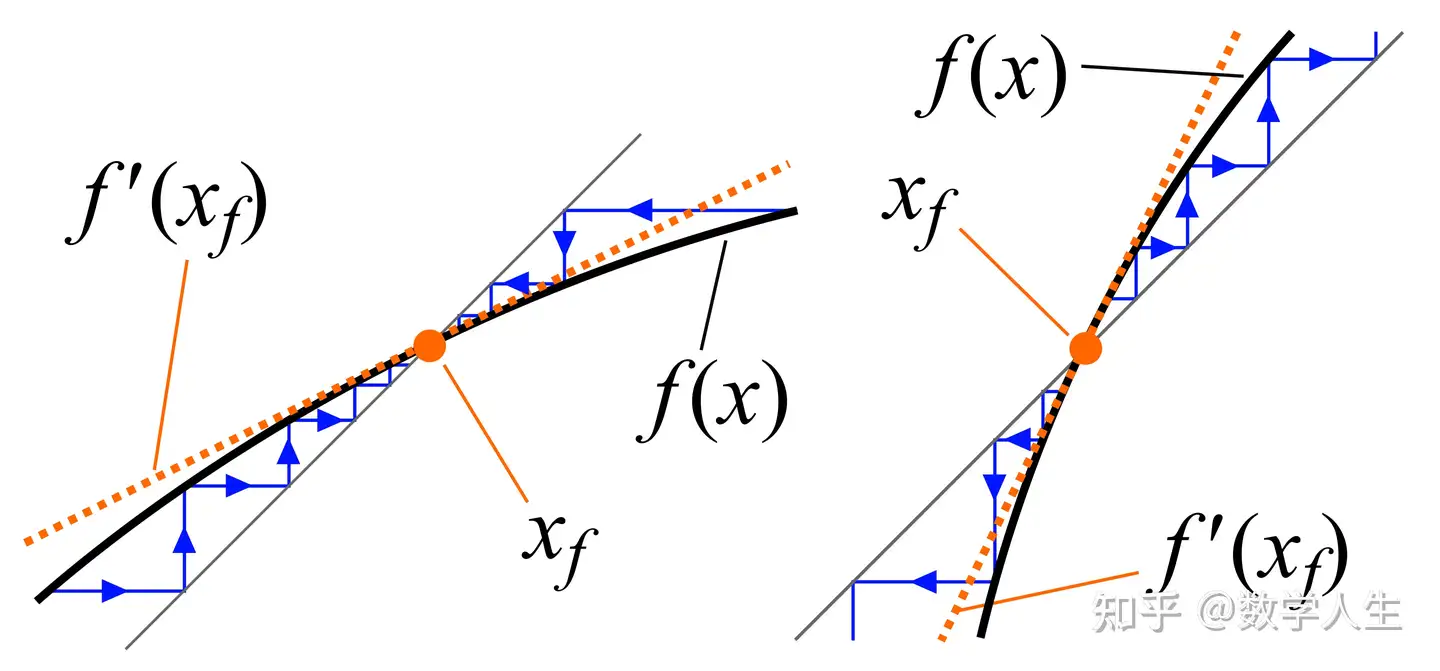
2. “规则”： 一个函数 f(x)。它定义了如何根据当前点 x 的位置，计算出下一个点 x_{n+1} = f(x_n)。这个函数通常是连续的，有时甚至是光滑的（可导的）。
3. “演员”： 一个初始点 x₀。
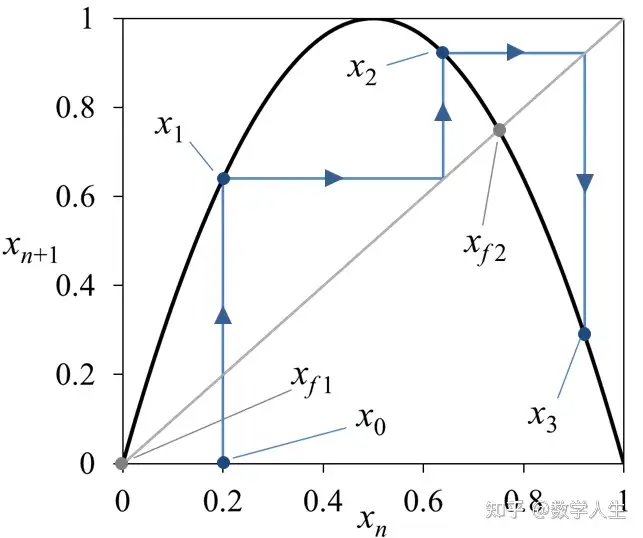
4. “剧情”： 点运动的轨迹 x₀, x₁ = f(x₀), x₂ = f(x₁) = f(f(x₀)), x₃ = f(f(f(x₀))), ...。这个序列 {x₀, x₁, x₂, ...} 称为轨道。
研究什么？关键问题：
- 不动点： 有没有点
x*满足f(x*) = x*？这个点就像“黑洞”，一旦到达就永远停在那里。它是系统最简单的稳定状态。 - 周期点： 有没有点
x_p满足f(f(...f(x_p)...)) = x_p（应用k次后回到自身）？这样的点会产生一个循环往复的轨道(x_p, f(x_p), f²(x_p), ..., f^{k-1}(x_p), x_p, ...)，称为周期k轨道。这代表了系统的周期性行为。 - 吸引子： 大多数初始点的轨道最终会趋向于什么样的状态？是一个不动点？一个周期轨道？还是一个更复杂的、永不重复但被限制在某个区域的集合（混沌吸引子）？吸引子代表了系统长期行为的模式。
- 对初始条件的敏感性（蝴蝶效应）： 这是混沌的核心特征。两个非常非常接近的初始点
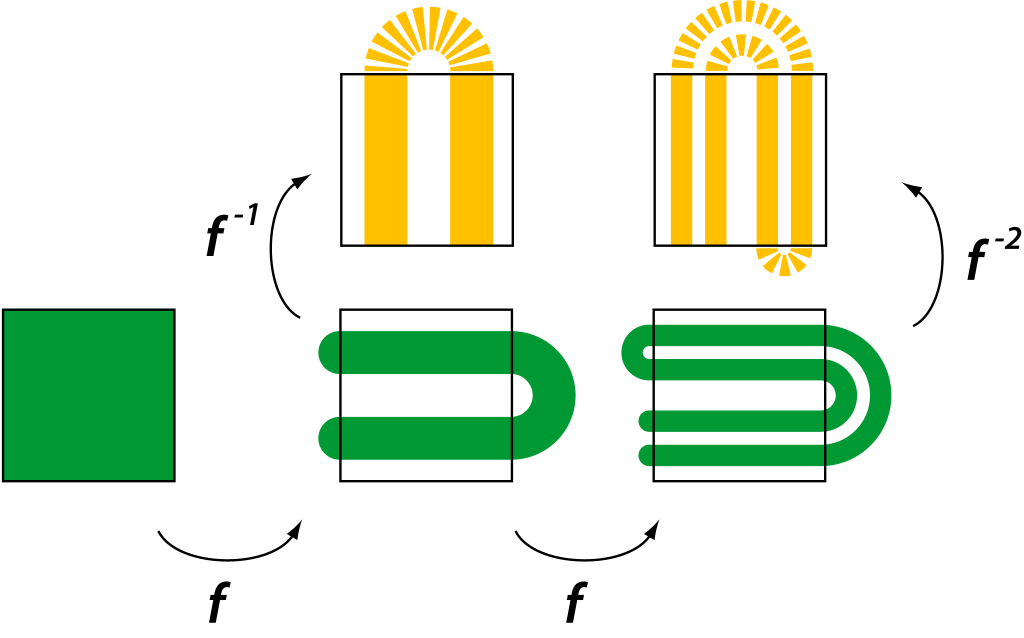
x₀和y₀，经过多次迭代后，它们的轨道{x_n}和{y_n}会分道扬镳，变得毫无关系吗？如果系统具有这种性质，那么长期预测就变得极其困难。 - 拓扑共轭： 两个看起来不同的规则
f(x)和g(x)，是否本质上描述了相同的动力学行为？就像一个故事用中文和英文讲述，情节一样，只是语言不同。找到这种“等价关系”有助于对系统分类。 - 分岔： 当规则
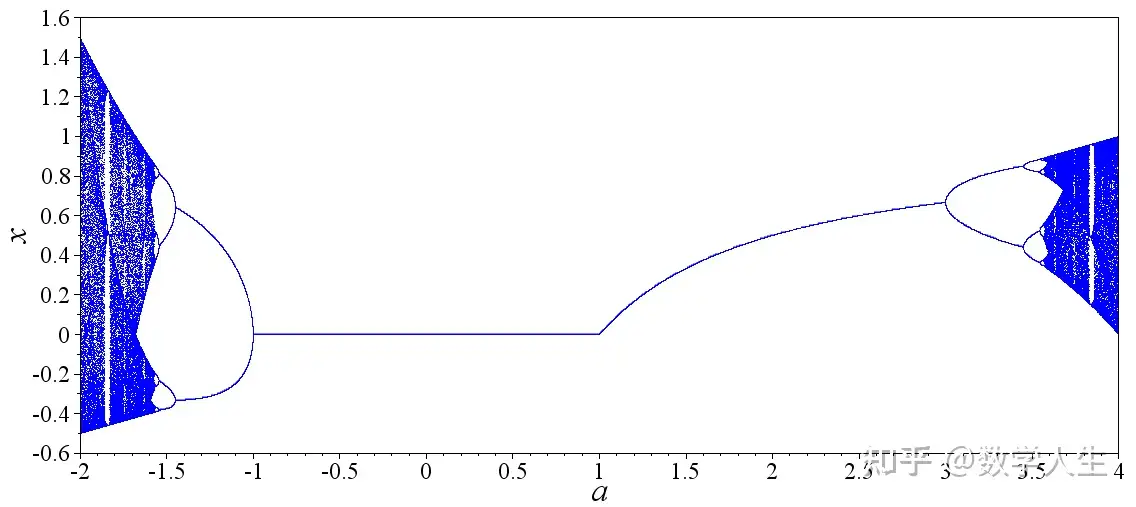
f(x)依赖于某个参数a（比如f_a(x) = a * x * (1 - x)）时，随着a的变化，系统的长期行为（吸引子的类型、数量、稳定性）会发生突然的、戏剧性的变化。这就像调节一个旋钮，系统性质突然“跃变”了。
一个著名的例子：Logistic Map（逻辑斯蒂映射）
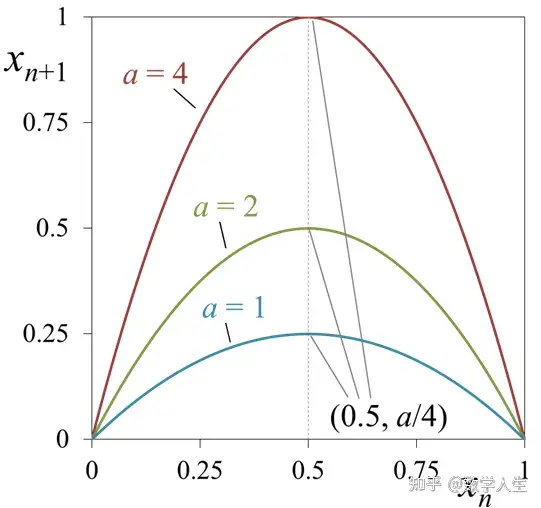
规则极其简单：f(x) = r * x * (1 - x)。其中 x 在 [0, 1] 区间内（比如可以代表种群数量占环境最大承载量的比例），r 是一个参数（比如代表繁殖率）。
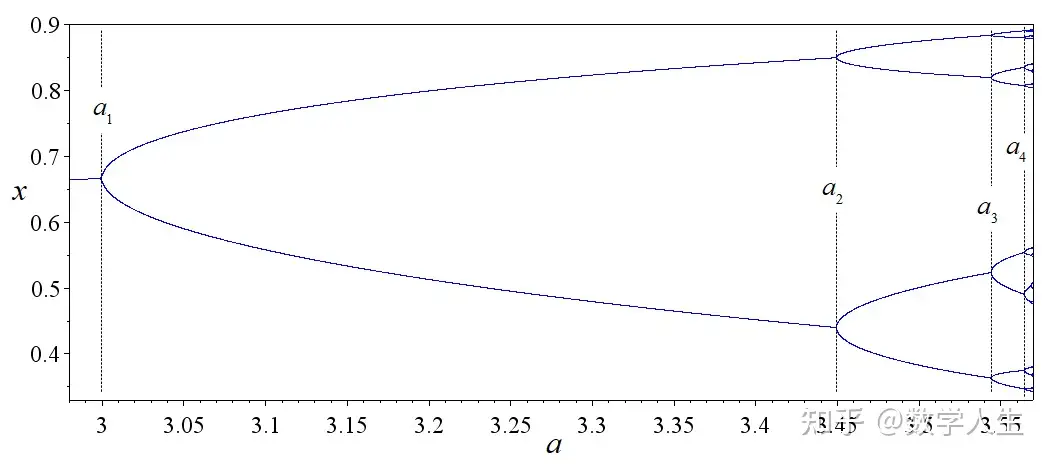
- 当
r比较小（比如r=2）时：几乎所有初始点的轨道都趋向于一个稳定的不动点。种群数量最终稳定在一个固定值。 - 当
r增大一些（比如r=3.2）时：不动点失稳，出现一个稳定的周期2轨道。种群数量开始呈现“大小年”交替振荡。 - 当
r继续增大（比如r=3.5）时：周期2失稳，出现稳定的周期4轨道。振荡模式变得更复杂。 - 当
r增大到某个临界值（约r≈3.57）以上：系统进入混沌区！轨道看起来是随机的（虽然由完全确定的规则产生），永不重复，对初始条件极其敏感。种群数量变化变得不可长期预测。在这个区域里，还能发现一些“窗口”，其中又会出现稳定的周期轨道（比如周期3）。 - 当
r=4时：混沌行为充满整个区间[0, 1]，并且轨道点会稠密地分布在整个区间。
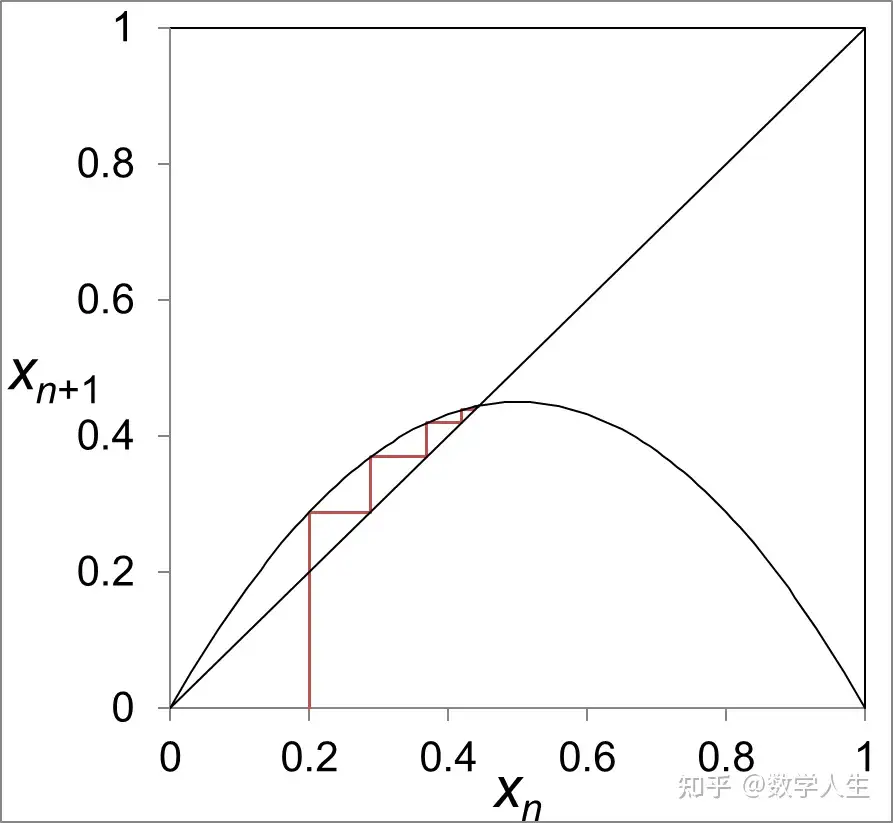
这个简单的二次函数，仅仅通过改变一个参数 r，就展现了从稳定、周期振荡到混沌的几乎所有一维动力系统的典型行为！它是一维动力系统研究的“明星模型”。
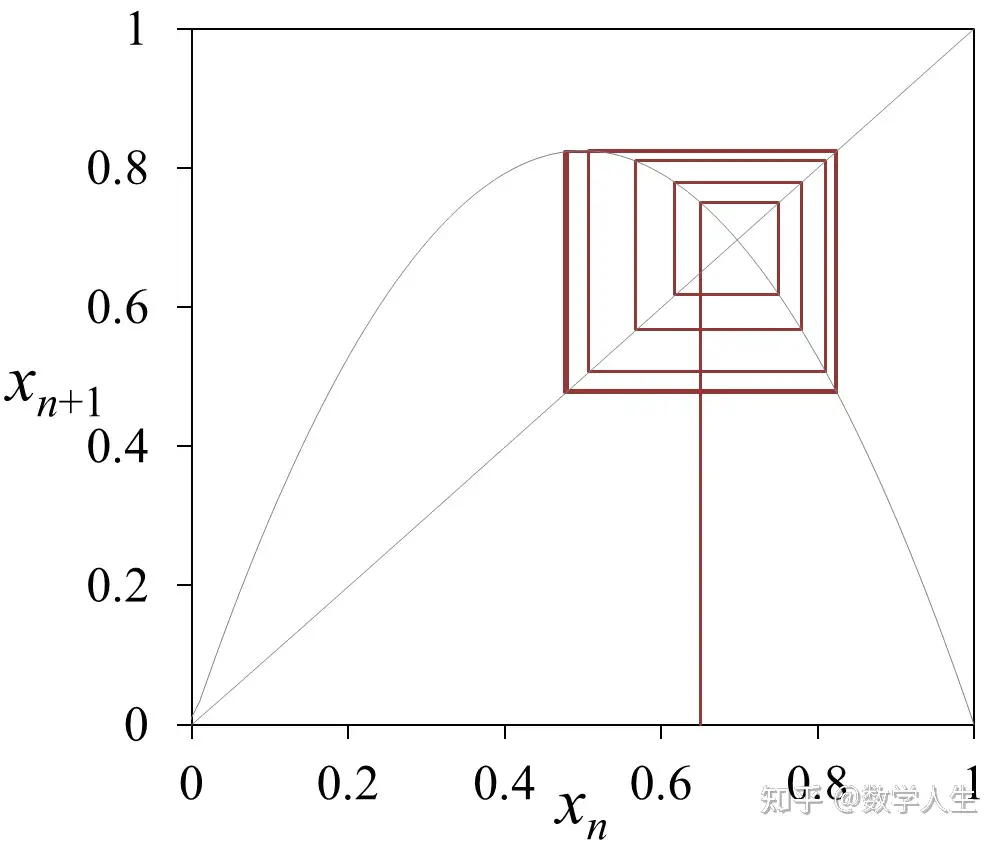
一维动力系统研究的是点在一条线（直线段或圆圈）上，按照一个确定的规则 f(x) 一步步移动的长期行为。它关注点最终会去哪里（吸引子）、是否会周期性重复、是否对起点极其敏感（混沌），以及当规则参数变化时行为如何突变（分岔）。虽然空间结构简单，但它能产生极其丰富和复杂的动力学现象，是理解更复杂系统的基础，并且在简化模型中描述了许多自然和社会现象。Logistic Map 是展示一维动力系统魅力最经典的例子。
；
；
，如图所示。
表示向前，
表示左转 
表示右转 
。也就是说，每一次的迭代，都会使得总的长度变成原来的 
倍。由于
，
个大小一致且互不重叠的小物体组成，这些小物体的形状和这个物体本身相同。若这些小物体和大物体的大小比例为 
，也就是说小物体放大 
倍之后与大物体完全重合，那么这个几何物体的 Hausdorff 维度（豪斯多夫维数）就定义为 
，
。
的线段可以被分成 
段（
），每段的长度与原来线段的大小比例是 
（
），因此 Hausdorff 维度是 
。
个边长是 
的小正方形，每一个小正方形与原来正方形的大小比例是 
。
个边长是 
。
。
。
。
是初始三角形的面积，
表示第 $n$ 次迭代的三角形面积，其中 
。
条，在第一次迭代的时候会生成三个小三角形，每一个小三角形的面积是初始的 
，同时从 
条边。也就是说：
。
，同时从 
条边。也就是说：
。
。
，考察其定义域的点 
的 
，进一步可以研究 
的极限。
（![a\in[0,2\pi]](https://s0.wp.com/latex.php?latex=a%5Cin%5B0%2C2%5Cpi%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
）的 Julia 集合的动图如下：
的偶数和复数 
使得 
的 Julia 集合 
是正测度？
.
is a 
-periodic 
-function.
because they are concrete examples of continuous but nowhere differentiable functions.
tends to be a “fractal object” because 
-function for all 
. In fact, for all ![{x,y\in[0,1]}](https://s0.wp.com/latex.php?latex=%7Bx%2Cy%5Cin%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0 "{x,y\in[0,1]}")
, we have
, i.e., 
.![{f:[0,1]\rightarrow\mathbb{R}}](https://s0.wp.com/latex.php?latex=%7Bf%3A%5B0%2C1%5D%5Crightarrow%5Cmathbb%7BR%7D%7D&bg=ffffff&fg=000000&s=0 "{f:[0,1]\rightarrow\mathbb{R}}")
is
, the Hölder continuity condition
by the family 
of rectangles given by![\displaystyle R_{j,n}:=\left[\frac{j-1}{n}, \frac{j}{n}\right] \times \left[f(j/n)-\frac{C}{n^{\alpha}}, f(j/n)+\frac{C}{n^{\alpha}}\right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+R_%7Bj%2Cn%7D%3A%3D%5Cleft%5B%5Cfrac%7Bj-1%7D%7Bn%7D%2C+%5Cfrac%7Bj%7D%7Bn%7D%5Cright%5D+%5Ctimes+%5Cleft%5Bf%28j%2Fn%29-%5Cfrac%7BC%7D%7Bn%5E%7B%5Calpha%7D%7D%2C+f%28j%2Fn%29%2B%5Cfrac%7BC%7D%7Bn%5E%7B%5Calpha%7D%7D%5Cright%5D&bg=ffffff&fg=000000&s=0 "\displaystyle R_{j,n}:=\left[\frac{j-1}{n}, \frac{j}{n}\right] \times \left[f(j/n)-\frac{C}{n^{\alpha}}, f(j/n)+\frac{C}{n^{\alpha}}\right]")
. In fact, since 
for each 
, we have
. Because 
. Of course, this bound is certainly suboptimal for 
(because we know that 
anyway).Fortunately, we can refine the covering 
by taking into account that each rectangle 
tends to be more vertical than horizontal (i.e., its height 
is usually larger than its width 
). More precisely, we can divide each rectangle 
squares, say
has diameter 
. In this way, we obtain a covering 
of 
such that
. Since 
integer and for all 
a 
such that
.
such that
.
and 
is large.
for all 
. In particular, if 
is an invariant repeller for the endomorphism 
given by
led Ledrappier to the following criterion for the validity of Mandelbrot’s conjecture when 
the alphabet 
. The unstable manifolds of 
through 
, 
, and
of the Bernoulli measure 
on 
(induced by the discrete measure assigning weight 
to each letter of the alphabet 
of the expanding endomorphism 
,
and 
. In plain terms, this means that
-invariant probability measure which is absolutely continuous along unstable manifolds (see 
have important consequences for the fractal geometry of the graph 
, i.e.,
has Hausdorff dimension
. By 
supported on 
. Finally, the main point is that the assumptions in Ledrappier theorem allow to prove that the measure 
given by the lift to ![{[0,1]}](https://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0 "{[0,1]}")
via the map 
satisfies
, then
for Lebesgue almost every 
for almost every 
implies that 
, 
and 
, we say that two infinite words 
are 
-transverse at 
if either
, 
are 
, 
are 
; otherwise, we say that 
and 
are
;
.
integer such that 
, then
are mutually transverse, so that they almost fill a small neighborhood 
of some point 
and 
, one has 
. Indeed, once we know that 
, they can apply Tsujii’s theorem and Ledrappier’s theorem (or rather Corollary 
. If 
and 
) requires the introduction of a modified version of Tsujii’s transversality condition: roughly speaking, Shen defines a function 
(inspired from 
for some integer 
;
.
, the series defining 
converges faster than the series defining 
.
, then
as follows. Take 
, and let 
be such that 
distinct elements listed in such a way that
, where 
.
if 
;
;
as 
, and 
as 
).
.
, the previous estimate implies that
, 
, we say that an interval 
is symmetric if 
where ![\tau:[-1,1]\rightarrow [-1,1]](https://s0.wp.com/latex.php?latex=%5Ctau%3A%5B-1%2C1%5D%5Crightarrow+%5B-1%2C1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
is so that 
and 
if 
. Furthermore, for each symmetric interval 
let 
be the minimal positive integer with 
and let
the Poincare map or transfer map to 
to ![f:[-1,1]\rightarrow [-1,1]](https://s0.wp.com/latex.php?latex=f%3A%5B-1%2C1%5D%5Crightarrow+%5B-1%2C1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
be a unimodal map with one non-flat critical point with negative Schwarzian derivative and without attracting periodic points. Then there exists 
and a sequence os symmetric intervals 
around the turning point which shrink to 
such that 
contains a 
scaled neighbourhood of 
and such that the following properties hold.
is constant.
be a component of the domain 
such that 
is monotone, 
and 
. Here 
is the transfer time on 
.
such that
to 
.
can be written as 
where the distortion of 
is universally bounded by 
(Here 
) has either zero or full Lebesgue measure. An alternative way to define this notation of ergodicity goes as follows: 
such that 
has Lebesgue measure zero, at most one of these sets has positive Lebesgue measure. (Here 
.)
, 
for almost all 
(in which case it is called a solenoidal attractor);
do not have such Cantor attractors. Moreover, Lyubich has shown that these absorbing Cantor attractors can not exist if the critical point is quadratic. However, Bruin, Keller, Nowicki and Van Strien showed that the absorbing Cantor attractors exist for Fibonacci maps when the critical order 
is sufficiently large enough.
unimodal, has a quadratic critical point, has negative Schwarzian derivative and has no periodic attractors, then each closed forward invariant set 
to be the maximal interval on which 
is monotone. Let 
and 
be the components of 
and define 
be the minimum of the length of 
and 
.
for almost all 
of 
such that for almost every 
of 
is monotone, 
and 
.
or 
is 
, with a bound on the first and the second derivatives. Assume that the interval ![[q_{0},q_{k}]](https://s0.wp.com/latex.php?latex=%5Bq_%7B0%7D%2Cq_%7Bk%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
( or ![[q_{0},q_{\infty}]](https://s0.wp.com/latex.php?latex=%5Bq_%7B0%7D%2Cq_%7B%5Cinfty%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
) is positive invariant, so ![f(x)\in [q_{0},q_{k}]](https://s0.wp.com/latex.php?latex=f%28x%29%5Cin+%5Bq_%7B0%7D%2Cq_%7Bk%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
for all ![x\in [q_{0}, q_{k}]](https://s0.wp.com/latex.php?latex=x%5Cin+%5Bq_%7B0%7D%2C+q_%7Bk%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
( or ![f(x)\in [q_{0},q_{\infty}]](https://s0.wp.com/latex.php?latex=f%28x%29%5Cin+%5Bq_%7B0%7D%2Cq_%7B%5Cinfty%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
for all ![x\in[q_{0},q_{\infty}]](https://s0.wp.com/latex.php?latex=x%5Cin%5Bq_%7B0%7D%2Cq_%7B%5Cinfty%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
).
( or 
),assume that we have defined densities up to 
, then define define 
as follows
, which takes one density function to another function, is called the Perron-Frobenius operator. The limit of the first 
,
.
on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
. From the definition of 
, the slope on 
and 
are 1 and 2, respectively. If 
, then it has only one pre-image on 
, then it has two pre-images, one is 
in 
in 
, then
. By induction, 
on 
. Therefore, 
on 
. By similar considerations,
and 
for all 
and 
for all 
![A=[a_{ij}]](https://s0.wp.com/latex.php?latex=A%3D%5Ba_%7Bij%7D%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
be a 
matrix. We say 
for all 
. Such a matrix is called irreducible if for any pair 
such that 
where 
is the 
th element of 
. The matrix 
such that no eigenvalue of 
.
and a non-negative right (column) eigenvector 
.
, 
all 
).
.
has the largest absolute value in the set of all eigenvalues of 
for all pairs 
. That means 
is a strictly positive 
be a compact interval. A 
map 
is called Markov if there exists a finite or countable family 
of disjoint open intervals in 
has Lebesgue measure zero and there exist 
and 
such that for each 
and each interval 
such that 
is contained in one of the intervals 
one has
, then 
;
such that 
for each 
. Usually, we will denote the Lebesgue measure of a Borel set 
.
be corresponding partition. Then there exists a 
invariant probability measure 
on the Borel sets of 
is uniformly bounded and Holder continuous. Moreover, for each 
one has 
for some 
for every Borel set 
.
for each interval ![f_{a}(x)=ax(1-x), a\in[0,4]](https://s0.wp.com/latex.php?latex=f_%7Ba%7D%28x%29%3Dax%281-x%29%2C+a%5Cin%5B0%2C4%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
, ![f_{a}:[0,1]\rightarrow [0,1]](https://s0.wp.com/latex.php?latex=f_%7Ba%7D%3A%5B0%2C1%5D%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
.![\{ a\in[0,4]: f_{a} \text{ satisfies Axiom A} \}](https://s0.wp.com/latex.php?latex=%5C%7B+a%5Cin%5B0%2C4%5D%3A+f_%7Ba%7D+%5Ctext%7B+satisfies+Axiom+A%7D+%5C%7D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
是否在 [0,4] 中稠密？
满足 Axiom A 
和 
不是拓扑共轭的，即使它们的 Kneading 序列是一样的。
.
和 
拓扑同胚，则有 
在这里 
都是复平面上面的连通开集, 
是保持定向的同胚映射，称 
), 如果
是 ACL 的，也就是线段上绝对连续，absolutely continuous on lines.
几乎处处成立。
有
几乎处处成立。
则 
![a_{0} \in (0,4]](https://s0.wp.com/latex.php?latex=a_%7B0%7D+%5Cin+%280%2C4%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
![Comb(a_{0})=\{ a\in(0,4]: K(f_{a})=K(f_{a_{0}}) \},](https://s0.wp.com/latex.php?latex=Comb%28a_%7B0%7D%29%3D%5C%7B+a%5Cin%280%2C4%5D%3A+K%28f_%7Ba%7D%29%3DK%28f_%7Ba_%7B0%7D%7D%29+%5C%7D%2C&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
![Top(a_{0})= \{ a\in (0,4]: f_{a} \text{ and } f_{a_{0}} \text{ are topological conjugate } \},](https://s0.wp.com/latex.php?latex=Top%28a_%7B0%7D%29%3D+%5C%7B+a%5Cin+%280%2C4%5D%3A+f_%7Ba%7D+%5Ctext%7B+and+%7D+f_%7Ba_%7B0%7D%7D+%5Ctext%7B+are+topological+conjugate+%7D+%5C%7D%2C&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
![Qc(a_{0}) = \{ a\in (0,4]: f_{a} \text{ and } f_{a_{0}} \text{ are quasi-conformal conjugate} \},](https://s0.wp.com/latex.php?latex=Qc%28a_%7B0%7D%29+%3D+%5C%7B+a%5Cin+%280%2C4%5D%3A+f_%7Ba%7D+%5Ctext%7B+and+%7D+f_%7Ba_%7B0%7D%7D+%5Ctext%7B+are+quasi-conformal+conjugate%7D+%5C%7D%2C+&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
![Aff(a_{0}) = \{ a\in (0,4]: f_{a} \text{ and } f_{a_{0}} \text{ are linear conjugate} \},](https://s0.wp.com/latex.php?latex=Aff%28a_%7B0%7D%29+%3D+%5C%7B+a%5Cin+%280%2C4%5D%3A+f_%7Ba%7D+%5Ctext%7B+and+%7D+f_%7Ba_%7B0%7D%7D+%5Ctext%7B+are+linear+conjugate%7D+%5C%7D%2C+&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
没有双曲吸引或者中性周期轨，则 
![f:[0,1]\rightarrow [0,1]](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D%5Crightarrow+%5B0%2C1%5D+&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
是 
, 
是正整数，则存在![f_{n}:[0,1]\rightarrow [0,1]](https://s0.wp.com/latex.php?latex=f_%7Bn%7D%3A%5B0%2C1%5D%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
使得 ![|| f_{n}- f ||_{C^{k}}=\max_{x\in[0,1]} \max_{0\leq m\leq k} |D^{m}f_{n}(x)-D^{m}f(x)| \rightarrow 0](https://s0.wp.com/latex.php?latex=%7C%7C+f_%7Bn%7D-+f+%7C%7C_%7BC%5E%7Bk%7D%7D%3D%5Cmax_%7Bx%5Cin%5B0%2C1%5D%7D+%5Cmax_%7B0%5Cleq+m%5Cleq+k%7D+%7CD%5E%7Bm%7Df_%7Bn%7D%28x%29-D%5E%7Bm%7Df%28x%29%7C+%5Crightarrow+0&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
as 
, 这里的每个
都满足Axiom A。
是紧致度量空间，
是连续函数。如果
是使得
的最小正整数，则称x是以n为周期的周期点。
.
,
,
i.e. ![X=[0,1]](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
, ![f(x)\in C^{1}[0,1]](https://s0.wp.com/latex.php?latex=f%28x%29%5Cin+C%5E%7B1%7D%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
, 
是以n为周期的周期轨道， 定义乘子(multiplier) 
。
称为
是双曲周期轨。
称为中性周期轨。
称为双曲吸引轨。
称为双曲斥性轨。![f:[0,1]\rightarrow [0,1]](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D%5Crightarrow+%5B0%2C1%5D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
是
映射，A是紧集并且
使得对任意的
, 有
，则称A是双曲集。
,
是双曲吸引轨 
的吸引区域, ![\Omega=[0,1]\setminus \cup_{i=1}^{m}B(\theta_{i})](https://s0.wp.com/latex.php?latex=%5COmega%3D%5B0%2C1%5D%5Csetminus+%5Ccup_%7Bi%3D1%7D%5E%7Bm%7DB%28%5Ctheta_%7Bi%7D%29&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
是双曲集。
，1是双曲斥性不动点，0是双曲吸引不动点。
, ![\Omega=[-1,1]\setminus B(\{0\})=\{-1,1\}](https://s0.wp.com/latex.php?latex=%5COmega%3D%5B-1%2C1%5D%5Csetminus+B%28%5C%7B0%5C%7D%29%3D%5C%7B-1%2C1%5C%7D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
. 
, 
. 取
.
.
并且
. i.e. 
是
连续的，
如果A是双曲集，则A的Lebesgue测度是零。
的映射，
, 则存在双曲吸引周期轨 
使得 
f 满足 Axiom A。
,![\Lambda_{U} = \{ x\in[0,1]: f^{n}(x)\notin U, \forall n\geq 0 \}](https://s0.wp.com/latex.php?latex=%5CLambda_%7BU%7D+%3D+%5C%7B+x%5Cin%5B0%2C1%5D%3A+f%5E%7Bn%7D%28x%29%5Cnotin+U%2C+%5Cforall+n%5Cgeq+0+%5C%7D&bg=ffffff&fg=2b2b2b&s=1&c=20201002)
,
是双曲集。
be intervals and let l, r be the components of 
. Then the Cross Ratio is defined as
for some 
and 
, then 
for all 
.![I=[a,b]](https://s0.wp.com/latex.php?latex=I%3D%5Ba%2Cb%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
, 
is a 
and any n for which 
is a diffeomorphism one has the following. If 
contains a 
scaled neighbourhood of 
, then
which does not depend on f, n, and t such that
contains a 
. Then for any univalent function 
one has a universal function 
such that
is the unit disc on the complex plane 
, 
is a holomorphic function with 
. Then 
for all 
and 
Moreover, if 
for some 
or 
then 
for some 
is the unit disc on the complex plane 
is a holomorphic function, then
is the upper half plane of the complex plane 
is a holomorphic map. Then
, assume 
denotes the hyperbolic distance between 
and 
on 
for some points 
, then 
, where
is an interval. It is easy to show that 
is conformally equivalent to the upper half plane and define 
as
at which the discs intersect the real line. Moreover, 
Define
is a holomorphic map, then 
is a real polynomial map, its critical points are on the real line. Assume 
is a diffeomorphism, then there exists a set 
such that 
and
is a conformal map.
and assume f maps the real line to the real line. For each 
there exists 
such that if J is a real interval in 
, then
is
is
, then the hyperbolic length of the interval 
on the total interval 
is
is a 
, then
be a 
, then there exists a unique 
such that 
for all 
. Therefore, assume that 
or 
for all 
. Since 
is a continuous function on the closed interval I, there exists 
such that 
for all 
.
such that 
. Since the schwarzian derivative of 
. However, from the definition of 
, we get
, there exists 
such that, if ![f: [-\tau, 1+\tau] \rightarrow \mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A+%5B-%5Ctau%2C+1%2B%5Ctau%5D+%5Crightarrow+%5Cmathbb%7BR%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
is a 
for all ![t\in [-\tau,1+\tau],](https://s0.wp.com/latex.php?latex=t%5Cin+%5B-%5Ctau%2C1%2B%5Ctau%5D%2C&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
then we have
Show that 
as 
(This recovers the classical Koebe non-linearity principle).
ZHANG RONG 