Mathematics

跨越百年的素数间隙之谜：最小间隔与最大间隔

Leave a comment

素数的呼吸：咫尺天涯与辽阔星河

在数字的汪洋中，素数如同散落的星辰，它们孤独地存在，除了自身和1，不被任何其他整数整除。它们的分布，是数学中最古老也最迷人的谜题之一。欧几里得早已证明，这星辰之河奔流不息，永无止境。然而，星辰之间的距离，却并非均匀。它们时而亲密依偎，时而相隔万里，仿佛宇宙本身在无声地呼吸。

素数表

为了证明素数有无穷多个，这里举两个常见的证明方法。

1. 欧几里得证明（反证法，公元前300年）

  • 思路：假设素数有限，构造一个新数导出矛盾。
  • 步骤：
    1. 假设素数只有有限个，记为 p_1, p_2, \dots, p_n。
    2. 构造新数 N = p_1 p_2 \cdots p_n + 1。
    3. N 不被任何 p_i 整除（因 N \equiv 1 \pmod{p_i})。
    4. 因此 N 是素数或含有新素因子，与假设矛盾。
  • 意义：最古老且简洁的证明，开创了反证法的经典应用。

2. 欧拉证明（分析学方法，18世纪）

  • 思路：利用调和级数发散和算术基本定理。
  • 步骤：
    1. 对调和级数取对数： \ln\left(\sum_{n=1}^\infty \frac{1}{n}\right) = \sum_{p} \ln\left(\frac{1}{1 - \frac{1}{p}}\right).
    2. 由调和级数发散 → 右端求和发散 → 素数个数无限。
  • 关键公式： \sum_{n=1}^\infty \frac{1}{n} = \prod_{p} \left(1 - \frac{1}{p}\right)^{-1}.
  • 意义：首次将分析与数论结合，启发了黎曼 \zeta 函数研究。

两个证明不仅确认了素数的无限性，更推动了数论和分析发展，体现了数学的多样性与统一性。

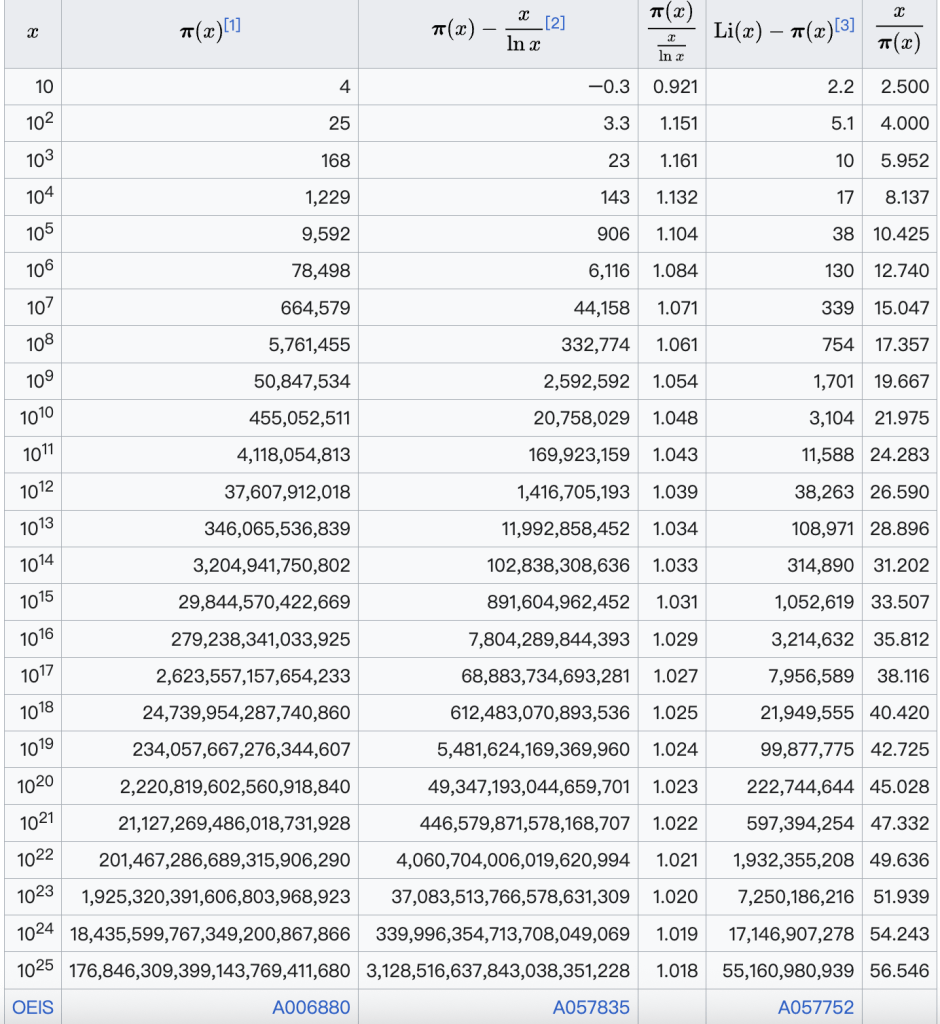
素数定理（Prime Number Theorem, PNT）是数论中描述素数分布渐进行为的核心定理，其揭示了素数在自然数中的密度规律。设 \pi(x) 表示不超过实数 x 的素数个数，则当 x \rightarrow \infty 时，有： \pi(x) \sim \frac{x}{\ln x}，其中符号 \sim 表示渐近等价，即： \lim_{x \to \infty} \frac{\pi(x)}{x / \ln x} = 1。通过数值的计算，我们可以直接得到下面的计算结果。

几个函数的对比结果

除此之外，素数定理还有以下等价表述，均描述相同的渐近行为：

对数积分形式（更精确）：

\pi(x) \sim Li(x) = \int_2^x \frac{dt}{\ln t}，其中 Li(x) 是对数积分函数，满足 Li(x) \sim \frac{x}{\ln x}。

切比雪夫函数形式：

定义 \theta(x) = \sum_{p \leq x} \ln p（对所有素数 p \leq x 的 \ln p 求和），则： \theta(x) \sim x。定义 \psi(x) = \sum_{n \leq x} \Lambda(n)（其中 \Lambda(n) 是冯·曼戈尔特函数，当 n = p^k 时 \Lambda(n) = \ln p，否则为 0），则： \psi(x) \sim x.

素数定理的直观解释。素数定理表明，当 x 极大时，x 附近的素数密度约为 \frac{1}{\ln x}。示例：

当 x = 10^6 时，\pi(x) \approx 78,498，而 x / \ln x \approx 72,382，比值约 1.085。

当 x = 10^9 时，\pi(x) \approx 50,847,534，x / \ln x \approx 48,254,942，比值约 1.053，更接近 $ latex 1$。

素数定理的历史意义：高斯（1792年）和勒让德（1798年）通过数值计算猜想 \pi(x) \sim \frac{x}{\ln x}。切比雪夫（1852年）证明 \frac{\pi(x)}{x / \ln x} 的极限若存在必为 1，并给出上下界

0.921 \leq \liminf \frac{\pi(x)}{x / \ln x} \leq \limsup \frac{\pi(x)}{x / \ln x}\leq 1.106。

阿达玛与德·拉·瓦莱·普桑（1896年）独立利用复分析（黎曼ζ函数非零区域）完成证明。塞尔伯格与埃尔德什（1949年）给出仅用实分析的初等证明。

素数定理与黎曼猜想的关系：素数定理等价于黎曼 \zeta 函数在 \Re(s) = 1 上无非平凡零点。黎曼猜想若成立，可将误差项优化为 \pi(x) =Li(x) + O(\sqrt{x} \ln x)。狄利克雷定理（算术级数中的素数分布）是素数定理在模 q 余 a（\gcd(a,q)=1）素数集上的推广。

素数定理以简洁公式 \pi(x) \sim \frac{x}{\ln x} 揭示了素数的宏观分布规律，成为解析数论的基石，其证明融合了复分析与深刻数论思想，影响深远。

咫尺之间：孪生之梦

最令人心动的亲密，莫过于“孪生素数”——像（3,5）、（11,13）、（17,19）这样，仅相差2的素数对。它们如同双生子，在数轴上紧紧相随。孪生素数猜想断言：这样的“双生子”有无穷多对。它直观得近乎理所当然，却让最聪慧的头脑困扰了数百年。

孪生素数

长久以来，数学家们只能步步逼近。假设 p_{n} 表示第 n 个素数，那么相邻素数的间距就是 p_{n+1}-p_{n}。当 m\geq 1 是正整数的时候，定义 H_{m}=\liminf_{n\rightarrow +\infty}(p_{n+m}-p_{n})，那么 H_{1}=2 就是孪生素数猜想。

从历史发展的历程来看，数学家A. de Polignac提出猜想：对于任意偶数 2k，存在无穷多对相邻素数，其差恰好为 2k。这为后续研究提供了方向，后续称之为1849年 Polignac猜想。

在1919年，挪威数学家V. Brun证明孪生素数倒数和收敛（Brun常数），并开创现代筛法。孪生素数的倒数和是数论中关于素数分布的一个重要结论。该结论揭示了孪生素数（即相差 2 的素数对，如 (3,5)、(11,13)）的分布特征，其核心内容如下：

设 \mathcal{P}_2 为所有孪生素数对 (p, p+2) 的集合，则其倒数和收敛： \sum_{(p,p+2) \in \mathcal{P}_2} \left( \frac{1}{p} + \frac{1}{p+2} \right) < +\infty. 该级数的极限值称为 布鲁恩常数（Brun’s constant），记为 B_2： B_2 \approx 1.902160583104 \ldots。

孪生素数的倒数和与素数倒数和对比：所有素数的倒数和发散（即 \sum_{p} \frac{1}{p} \to \infty），而孪生素数的倒数和收敛。这表明孪生素数比全体素数稀疏得多，即使孪生素数有无穷多对（孪生素数猜想尚未证明），其分布密度也足够低以保证倒数和有限。收敛性说明孪生素数的分布满足： \pi_2(x) := \#\{ p \leq x \mid p, p+2 \in \mathbb{P}\} \ll \frac{x}{(\ln x)^2}， 即孪生素数的数量增长慢于 \frac{x}{(\ln x)^2}（对比素数定理 \pi(x) \sim \frac{x}{\ln x}）。

布鲁恩的证明基于改进的筛法理论，核心步骤如下：

  1. 筛法构造：定义集合 S(x) 为所有不大于 x 的正整数 n 所组成的集合，这些 n 满足的条件是：对于所有小于 \sqrt{x} 的素数 p，p 既不整除 n，也不整除 n+2。则 \pi_2(x) \leq |S(x)| + O(\sqrt{x})。
  2. 上界估计：布鲁恩通过组合计数证明： |S(x)| \leq C \cdot \frac{x}{(\ln x)^2}，其中 C为常数，具体推导利用容斥原理和不等式放缩（如切比雪夫边界）。
  3. 倒数和收敛：由 \pi_2(x) \ll \frac{x}{(\ln x)^2} 可得： \sum_{p,p+2 \in \mathbb{P}} \frac{1}{p} \leq \sum_{k=1}^{\infty} \frac{\pi_2(2^k) - \pi_2(2^{k-1})}{2^{k-1}} \ll \sum_{k=1}^{\infty} \frac{1}{k^2} < \infty.

对前 N 个孪生素数对计算部分和： B_2(N) = \sum_{\substack{p \leq N \\ p, p+2 \in \mathbb{P}}} \left( \frac{1}{p} + \frac{1}{p+2} \right). 例如：当N = 10^6 时，B_2 \approx 1.518；当N = 10^{16} 时，B_2 \approx 1.902。针对收敛速度这个问题，因 \pi_2(x) \sim C_2 \frac{x}{(\ln x)^2}（C_2 \approx 1.32 为孪生素数常数），级数收敛极慢，需极大 N 才能接近 B_2。

布鲁恩定理以简洁而深刻的结论揭示了孪生素数分布的稀疏性，其证明融合了筛法与组合数学的精妙思想，成为解析数论的里程碑之一。该结论不仅推动了素数分布理论的进展，也在计算科学中留下有趣印记。

除此之外，布鲁恩还首次证明存在无穷多对9-殆素数（9-almost primes）的差为2（即“9+9”）。在1947年匈牙利数学家A. Rényi证明：存在常数 k，使得有无穷多对素数 p 和 k-殆素数 m，其差为2（即“k+1”）。在1966年，E. Bombieri与H. Davenport证明孪生素数密度上界：\pi_2(x) \leq 8C_2 (\ln x)^{-2}，表明孪生素数分布稀疏，后人称之为Bombieri-Davenport上界。在1978年，中国数学家陈景润证明：存在无穷多对素数 p 和2-殆素数 m，其差为2（即“1+2”），将筛法推向顶峰。在2005年，D. Goldston、J. Pintz和C. Yildirim证明：两个素数之间的间隙相比平均值可任意小。在强猜想假设（GEH）下，存在无穷多对素数差不超过16。

一个关键的突破来自张益唐教授。2013年，这位沉寂多年的学者带来震撼：存在无穷多对素数，它们的距离小于一个固定的数字——7000万。这个数字看似庞大，在无限的尺度下却微不足道。它如同在黑暗中凿开一道缝隙，证明素数并非总是疏离。在2013年4月，张益唐在《数学年刊》发表《素数间的有界间隔》，英文名是《Bounded Gaps between Primes》。首次严格证明：存在无穷多对素数对 (p, q)，其差不超过7000万（即 p_{n+1} - p_n < 7 \times 10^7）。这一成果解决了弱哥德巴赫猜想的关键部分。

随后，数学界的“接力赛”开启，陶哲轩领导的“博学者计划”和其他数学家（如詹姆斯·梅纳德）不断优化工具，将这个距离极限压缩到了令人惊叹的246。我们离证明孪生素数猜想（距离为2）依然遥远，但曙光已现。这咫尺之遥的探索，揭示了素数分布中深藏的、难以捉摸的规律性。在 2013年5–6月，常数优化热潮开启，张益唐的成果引发全球数学家合作优化常数：

  • 5月28日：降至6000万
  • 5月31日：降至4200万
  • 6月2日：降至1300万
  • 6月5日：降至40万
  • 2013年底：Polymath项目结合James Maynard新方法，将常数降至246。

到了2013年11月，James Maynard 在素数有界间距上取得了独立突破。James Maynard独立提出更简方法，将素数差常数降至600，并证明：对任意 k \geq 1，存在常数 C_k，使得无穷多对素数差不超过 C_k（Polymath项目进一步优化至246）。

2015年至今：后续进展Polymath8b项目给出精细上界公式：\pi_2(x) \leq C \frac{x}{(\ln x)^2}，并探索广义孪生素数分布。

素数小间距的关键结论如下：

  • 核心问题：素数间距能否无限小？孪生素数猜想（差为2）是否成立？
  • 核心工具：筛法（Brun–Selberg）、指数和（Goldston–Pintz–Yildirim）、张益唐的松弛筛法结合Bombieri–Vinogradov定理。
  • 未解难题：孪生素数猜想（\liminf_{n \to \infty} (p_{n+1} - p_n) = 2）仍未完全证明，但246已是迄今最佳上界。

辽阔星河：自由的旷野

然而，素数的呼吸并非只有浅吟低唱。它们也渴望辽阔的空间。你能想象在数轴上找到任意长的、完全没有素数的“荒漠”吗？答案是肯定的。

一个巧妙的构造揭示了这种自由：考虑一串连续的数字：n! + 2, n! + 3, n! + 4, …, n! + n。对于任意大于1的整数k（k ≤ n），n! + k 都能被k整除（因为n!包含k）。因此，这串长达n-1个连续数字中，没有一个是素数！随着n的增大，这片“荒漠”可以任意延长。这意味着，素数之间的间隔，可以像宇宙膨胀一样，变得无比巨大。

数学家们不满足于此，他们想知道这间隔到底能有多大。埃尔德什等数学家用更精密的工具证明：在小于某个巨大数字X的范围内，必然存在相邻素数，其间隔远大于它们的“平均间隔”（约为ln X）。具体来说，这个最大间隔至少可以像 (ln X * ln ln X * ln ln ln ln X) / (ln ln ln X) 那样增长（尽管公式复杂，它描绘了一种远超平均的、爆发式的增长）。这如同在星辰之河中，存在着难以想象的辽阔寂静地带。

素数大间距（Big Gaps）研究素数间隔的渐进增长，其难度不亚于素数的小间距。在1931年，Westzynthius的开创性工作结果证明存在无穷多个素数间隔大于 \log p_n，即：

\limsup_{n\to\infty} \frac{p_{n+1}-p_n}{\log p_n} = \infty。

首次确立素数间隔可无限超越对数尺度。

在1935年，Erdős将上述结果进行改进。他引入新方法，证明：

\limsup_{n\to\infty} \frac{p_{n+1}-p_n}{\log p_n \cdot \frac{\log\log p_n}{(\log\log\log p_n)^2}} > 0。

Erdős首次在分母中引入三重对数项，显著提升下界。

在1938年：Rankin的又取得了重大突破。优化常数并引入四重对数项：

\limsup_{n\to\infty} \frac{p_{n+1}-p_n}{\log p_n \cdot \frac{(\log\log p_n) \cdot (\log\log\log\log p_n)}{(\log\log\log p_n)^2}} > c+o(1)。

证明下界常数可大于 1（后经Pintz等优化至 c = 2e^\gamma）。其结果长期未被超越，成为经典基准。

到了2014年：Ford–Green–Konyagin–Tao–Maynard的革命性进展，彻底改进渐进阶：

\limsup_{n\to\infty} \frac{p_{n+1}-p_n}{\frac{\log p_n \cdot \log\log p_n \cdot \log\log\log\log p_n}{\log\log\log p_n}} \geq c > 0。

首次将分母降为 \log\log\log p_n，突破Rankin框架。

截至2024年，相邻素数的最大间距是：p_{n+1} - p_n = 1552（对应素数 p_n = 18,361,375,334,787）。上述渐进结果保证了间隔的无限增长，但具体数值依赖计算验证。素数大间距的发展历程体现了从初等证明到调和分析、组合数学的深度融合，尤其是2014年工作融合了多重数学工具，重塑了素数间隔的理论框架。

宇宙的韵律

素数的间距，就这样在“亲密无间”与“天各一方”之间摆荡。小间距（如孪生猜想）体现了素数分布潜在的某种“粘性”或聚集倾向；而大间距的存在，则彰显了其固有的、不可预测的随机性和自由。

数学家核心贡献
Green & Tao素数中存在任意长等差数列（Green-Tao 定理）。
张益唐素数间隙有界，开启小间隙研究。
Maynard独立优化间隙至 600；推广至多素数聚类；筛法创新。
Ford–Green–Konyagin–Tao–Maynard证明素数间隙可任意大（解决 Erdős–Rankin 猜想）。
Polymath协作优化间隙至 246，推动开放式数学研究。

这些成果共同推动了解析数论的突破，揭示了素数分布的深层结构，并为后续研究（如孪生素数猜想）奠定了基础。理解这些间距，就是试图破译宇宙在整数序列中留下的密码。张益唐的7000万、梅纳德的筛法革新、构造出的任意长荒漠、以及关于最大间隔的精密估计，都是人类智慧在探索这深邃韵律时留下的足迹。它们告诉我们，即使在最基础的数字序列里，也蕴藏着无限的惊奇——既有令人心安的亲密可能，也有挑战想象的辽阔自由。素数的呼吸，是数学宇宙永恒而迷人的心跳。

Leave a comment