笔者离开数学界已经八年时间，近期在 Arxiv 上翻阅资料的时候无意之中看到一篇关于复动力系统 Julia 集合正测度的文章。这篇文章是由 Avila 和 Lyubich 合写的，最终发表在 Annals of Mathematics（数学年刊）上，可以算是 Julia 集合正测度的最新进展。

[1] Avila, Artur, and Mikhail Lyubich. “Lebesgue measure of Feigenbaum Julia sets.” Annals of Mathematics 195.1 (2022): 1-88.

Julia 集合是由法国数学家 Gaston Julia 和 Pierre Fatou 在 20 世纪初提出的。Julia 集合通常用于研究复平面上的二次多项式迭代，即：f(z) = z^2 + c，其中 z 和 c 都是复数。

Julia 集合具有以下性质：

1. 分形结构：Julia 集合具有自相似的分形结构，即在任意放大的比例下，其局部结构与整体结构具有相似性。
2. 边界敏感：Julia 集合的边界对初始值非常敏感。在边界上的点，即使初始值有微小的改变，迭代结果也可能发生巨大变化。
3. 全分支：Julia 集合可以分为两类，一类是全分支的（connected），另一类是非全分支的（disconnected）。全分支的 Julia 集合（也称为 Fatou 集合）中的任意两点都可以通过一条路径连接；而非全分支的 Julia 集合则由许多分散的点组成。
4. 稳定集和逃逸集：Julia 集合可以划分为稳定集和逃逸集。稳定集中的点在迭代过程中保持有限，而逃逸集中的点在迭代过程中趋向于无穷大。
5. 复杂性：Julia 集合具有丰富的结构和高度复杂性。它们的形状取决于参数 c 的值，c 的不同取值会产生各种各样的 Julia 集合形状。
6. 与 Mandelbrot 集合的关系：Julia 集合和 Mandelbrot 集合之间存在密切的关系。对于给定的参数 c，如果 c 属于 Mandelbrot 集合，则相应的 Julia 集合是全分支的；否则，Julia 集合是非全分支的。

总之，Julia 集合在复动力系统中是一种独特且具有丰富性质的分形结构。

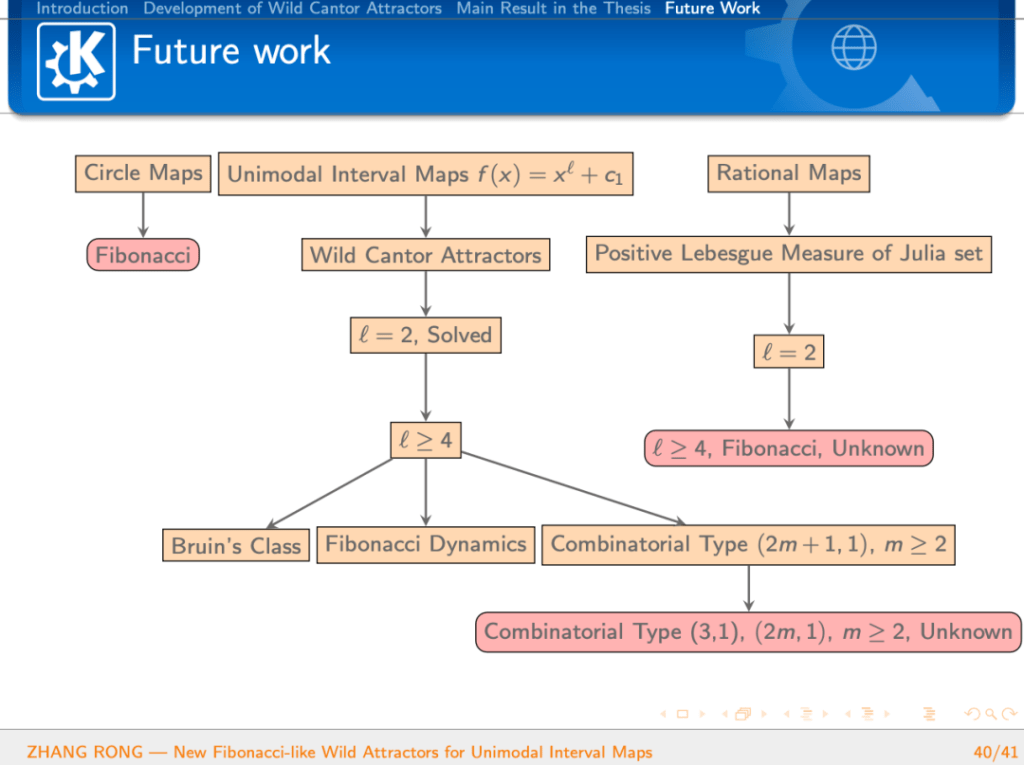
当年刚进入 NUS 的时候，从导师那里拿到的课题就是关于 Julia 集合正测度的，但是研究的对象并不是 2 次多项式（z -> z^2 + c），而是满足某种组合形式的高次多项式（z -> z^{\ell} +c）。

[2] Nowicki, Tomasz, and S. van Strien. “Polynomial maps with a Julia set of positive Lebesgue measure: Fibonacci maps.” preprint (1994).

这篇文章 [2] 有 90 页，但是里面有一个错误，Chapter 10 的一个定理证明出现了错误，导致这篇论文最终只挂在了 Arxiv 上，并没有正式发表。刚从导师那里拿到论文的时候，看到这篇文章足足有 90 页也觉得十分震惊，不过心想自己可能也能够坚持读下来。但是没想到彻底读完的时候，已经到了博士第三年上学期。相当于当时自己花费了差不多一两年时间在这篇论文上。数学家 Buff Xavier 也针对这篇文章写过一个法语的论文，指出了这篇论文的缺陷。但是我感觉这篇法语的文章并没有指出来哪一个章节证明错误了。

当年笔者为了阅读这篇文章，自然也读了周边的一系列文章，下面这篇文章同样是发表在 Annals of Mathematics（数学年刊）上。但是这是一篇关于实动力系统的文章，证明了 wild Cantor attractor 的存在性，其方法有希望应用到复动力系统领域，来最终证明 Fibonacci 多项式的 Julia 集合具有正测度。

[3] Bruin, Henk, et al. “Wild Cantor attractors exist.” Annals of mathematics (1996): 97-130.

可惜，遗憾的是，虽然这个方法在实动力系统上是成立了，论文也发表在 Annals of Mathematics 上，但是上述方法并不能够直接应用到复动力系统上，导致 Julia 集合的正测度一直是 Open Question。

但是，针对 2 次多项式的 Julia 集合的正测度研究，却一直有着不错的进展，而且每一篇文章都发表在数学的四大期刊上。

[4] Lyubich, Mikhail, and John Milnor. “The Fibonacci unimodal map.” Journal of the American Mathematical Society 6.2 (1993): 425-457.

这篇文章证明了 The quadratic unimodal map with Fibonacci combinatorial type has no wild Cantor attractor，发表在 JAMS 上。

[5] Lyubich, Mikhail. “Combinatorics, geometry and attractors of quasi-quadratic maps.” Annals of Mathematics 140.2 (1994): 347-404.

这篇文章证明了 Assume f is unimodal and has a quadratic critical point. If there exists a set X of positive Lebesgue measure so that for all x ∈ X, ω(x) is equal to a Cantor set C, then C is a solenoidal attractor and C = ω(c) for the critical point c. i.e. f has no wild Cantor attractor. 同样发表在 Annals of Mathematics 上。

[6] Buff, Xavier, and Arnaud Chéritat. “Quadratic Julia sets with positive area.” Annals of Mathematics (2012): 673-746.

后来到了 2012 年，有两位数学家证明了存在 2 次多项式使得它的 Julia 集合是正测度。到了 2022 年，数学家 Avila 和 Lyubich 又找到一类 2 次多项式，它们的 Julia 集合同样是正测度。这两篇论文都发表在 Annals of Mathematics 上。

如果没有记错的话，当年答辩的日子是 2015 年 4 月 24 日早上 10:00 – 11:00。在读博期间，笔者的博士课题从一开始就直接敲定，读书期间这个课题也没有进行过更换，那就是复动力系统里面的核心问题之一：

Open Question: Is the measure of Julia set of Fibonacci Polynomial positive or not?

事后回想起来，这个问题可能还是比较难，至少对我本人来说是太难了，可能已经超越了我能够把控的范围。阅读一篇有 Gap 的论文从某种层面打击到了自己的信心，导致后续我对这个问题根本不感兴趣，但是手上又没有其他课题可以做。有一次向导师提出了需要更换课题，但是被导师一口否决了，也只好沿着这个方向一直做下去。在一个没有讨价还价的读博环境下，无论导师提出什么样的学术要求，为了毕业我都会完成，但是坏处就是我对动力系统这个方向就完全失去了兴趣。

在答辩结束的那一天，虽然我不清楚以后可以做什么，但是我很明确地知道不要做什么。

近期，我也听到一些关于博士生和导师的说法：

1. 如果导师给博士生的题目是有答案的，那么导师对这个题目是不会感兴趣的；如果导师对这位博士生还有所期待，那么这个题目一定是暂时没有答案的；
2. 长期在某个方向工作的专家会有某种思维惯性，遇到问题的时候就不会朝着某个方向去思考。但是新人却有可能朝着某个方向做问题，反而解决了该领域的未知问题，同时给这个方向带来新的活力，因此 push 学生有助于将新人的潜力激发出来。如果没有在博士期间激发学生最大的潜力，那么确实是会留下遗憾的，并且也没有做到最好的自己；
3. 在读博期间，导师跟学生的关系并不是朋友的关系，而且导师布置的学术任务是要求学生一定要完成的，没有任何讨价还价的余地。

在导师靠谱的前提下，按照上述 3 点培养出来的学生，只有两种可能性：

• 科研做得很好，博士毕业之后完全具备独立科研能力，能够独立发表论文，成为科研新星；
• 直接离开学术界，毕竟上述博士科研经历基本上可以摧毁学生对科研的信心，毕竟课题有可能太难，导致学生无法完成这项任务。中等水平的学生也会知难而退，只有最优秀的学生有信心留在学术界。

虽然给博士生布置尚未解决的问题可以激发学生的创新能力和解决问题的能力，但过于困难的课题可能会导致学生在研究过程中消耗大量时间和精力，甚至可能会陷入困境。此外，并非所有导师都能充分了解学生的兴趣和能力，这可能导致题目设置与学生的实际需求脱节，从而降低研究效率。

虽然新人可能在解决问题时带来新思路和活力，但是新人可能由于知识储备和经验不足，在解决问题时更容易出现错误和偏差。

在读博期间，导师与学生之间的关系确实应该以学术任务为主，但将两者关系定义得过于严格可能会限制双方之间的沟通与交流。就相当于学生和导师只会交流学术，除此之外并没有任何可以沟通的其他内容，学生也不愿意和导师分享除了科研以外的任何事情。一个良好的导师-学生关系应当基于互相尊重、理解和支持的基础上，允许双方在学术任务以外的方面展开交流和合作。这种关系不仅有利于学术研究的开展，还有助于培养学生全面发展的能力。

后来工作了之后，我也会遇到一些困难，但是总能够有各种各样的方法来解决这个问题，与读博的时候死磕一个问题形成了鲜明的对比。在工作和生活中适时的妥协和退让，才会看到一个截然不同的风景，感受广阔无垠的天空。