(一)FTRL 的算法原理:
FTRL 算法综合考虑了 FOBOS 和 RDA 对于梯度和正则项的优势和不足,其特征权重的更新公式是:
上面的公式出现了 L2 范数,不过这一项的引入不会影响 FTRL 的稀疏性,只是使得求解结果更加“平滑”。通过数学计算并且放弃常数项可以得到上面的优化问题相当于求使得下面式子的最小的参数 W:
如果假设 上式等价于
写成分量的形式就是:
通过计算可以直接得到:
由此可以证明:引入 L2 正则化并没有对 FTRL 的稀疏性产生影响。
(二)学习率
在 SGD 的算法里面使用的是一个全局的学习率 ,意味着学习率是一个正数并且逐渐递减,对每一个维度都是一样的。而在 FTRL 算法里面,每个维度的学习率是不一样的。如果特征 A 比特征 B变化快,那么在维度 A 上面的学习率应该比维度 B 上面的学习率下降得更快。在 FTRL 中,维度 i 的学习率是这样定义的:
按照之前的定义 , 所以
(三)FTRL 算法
FTRL Algorithm
(1)输入,初始化
(2)for
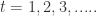
for
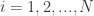
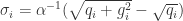
// equals to




end end
(四)Logistic Regression 的 FTRL 形式
在 Logistic Regression 中,假设 是 sigmoid 函数,
,需要预估
,那么 LogLoss 函数是
,
直接计算可得 ,所以 Logistic Regression 的 FTRL 算法就是:
FTRL Algorithm (Logistic Regression)
(1)输入,初始化
(2)for
for
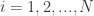
// gradient of loss function
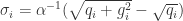
// equals to




end end

没写完?大帝你这个FTRL的objetive function有点丑啊。
Shai Shalev-Shwartz, ML界的名笔。他写了Online Learning 的survey,你可以参考一下。
Click to access OLsurvey.pdf
LikeLike
大帝,Objective function写的很丑啊。我看了半天才区分出loss function和regularizer。
Shai,ML界名笔,他写了一篇关于online learning 的survey。
Click to access OLsurvey.pdf
LikeLike