Let  be intervals and let l, r be the components of
be intervals and let l, r be the components of  . Then the Cross Ratio is defined as
. Then the Cross Ratio is defined as

Assume g is a  monotone function on the interval t, and g(t)=T, g(j)=J, g(l)=L, g(r)=R. Then define
monotone function on the interval t, and g(t)=T, g(j)=J, g(l)=L, g(r)=R. Then define

Define the Schwarzian Derivative for  function g,
function g,

Proposition 1. Assume f and g are  functions, then
functions, then
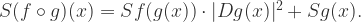

Proposition 2. If 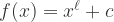 for some
for some  and
and 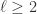 , then
, then  for all
for all  .
.
Proposition 3. Minimum Principle.
Assume ![I=[a,b]](https://s0.wp.com/latex.php?latex=I%3D%5Ba%2Cb%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) ,
,  is a
is a  diffeomorphism with negative schwarzian derivative, then
diffeomorphism with negative schwarzian derivative, then

Theorem 1. Real Koebe Principle.
Let Sf<0. Then for any intervals  and any n for which
and any n for which  is a diffeomorphism one has the following. If
is a diffeomorphism one has the following. If  contains a
contains a  scaled neighbourhood of
scaled neighbourhood of 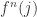 , then
, then

Moreover, there exists a universal function  which does not depend on f, n, and t such that
which does not depend on f, n, and t such that
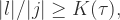
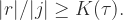
Theorem 2. Complex Koebe Principle
Suppose that  contains a
contains a  scaled neighbourhood of the disc
scaled neighbourhood of the disc  . Then for any univalent function
. Then for any univalent function  one has a universal function
one has a universal function  which only depends on
which only depends on  such that
such that

Theorem 3. Schwarz Lemma (Original Form)
Assume  is the unit disc on the complex plane
is the unit disc on the complex plane 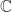 ,
,  is a holomorphic function with
is a holomorphic function with 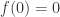 . Then
. Then 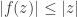 for all
for all  and
and  Moreover, if
Moreover, if  for some
for some 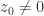 or
or 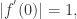 then
then  for some
for some 
Corollary 1.
Assume  is the unit disc on the complex plane
is the unit disc on the complex plane 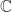 , and
, and 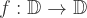 is a holomorphic function, then
is a holomorphic function, then


Corollary 2.
Assume 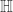 is the upper half plane of the complex plane
is the upper half plane of the complex plane 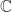 ,
,  is a holomorphic map. Then
is a holomorphic map. Then
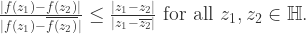

Corollary 3. Pick Theorem
The hyperbolic metric on  is
is  , assume
, assume  denotes the hyperbolic distance between
denotes the hyperbolic distance between  and
and  on
on  . Assume
. Assume  is a holomorphic function, then
is a holomorphic function, then

Moreover, if 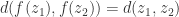 for some points
for some points  , then
, then  , where
, where

Background in hyperbolic geometry
Define

where  is an interval. It is easy to show that
is an interval. It is easy to show that  is conformally equivalent to the upper half plane and define
is conformally equivalent to the upper half plane and define  as
as

k is determined by the external angle 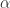 at which the discs intersect the real line. Moreover,
at which the discs intersect the real line. Moreover, 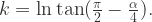 Define
Define

Corollary 4. (NS) Schwarz Lemma
(1) Assume 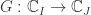 is a holomorphic map, then
is a holomorphic map, then 
(2) Assume  is a real polynomial map, its critical points are on the real line. Assume
is a real polynomial map, its critical points are on the real line. Assume  is a diffeomorphism, then there exists a set
is a diffeomorphism, then there exists a set  such that
such that  and
and
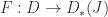 is a conformal map.
is a conformal map.
Corollary 5.
Assume  is a univalent map and D contains
is a univalent map and D contains  scaled neighbourhood of
scaled neighbourhood of  and assume f maps the real line to the real line. For each
and assume f maps the real line to the real line. For each  there exists
there exists  such that if J is a real interval in
such that if J is a real interval in  , then
, then
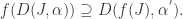
The Hyperbolic Metric On the Real Interval and Cross Ratio
As far as we know, the hyperbolic metric on the unit disc  is
is

Then the restriction to the real line is

Moreover, from it, we can deduce the hyperbolic metric on the real interval  is
is

If  , then the hyperbolic length of the interval
, then the hyperbolic length of the interval  on the total interval
on the total interval  is
is

where 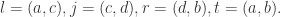
Theorem 4. Assume  is a
is a  diffeomorphism with negative schwarzian derivative. Assume
diffeomorphism with negative schwarzian derivative. Assume  , then
, then

That means f expands the hyperbolic metric on the real interval.
Proof. Since the schwarzian derivative of f is negative, 
Therefore,  That means f expands the hyperbolic metric on the real interval.
That means f expands the hyperbolic metric on the real interval.
Remark. From Schwarz-Pick Theorem, for a holomorphic map  ,
, 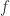 contracts the hyperbolic distance in the unit disc
contracts the hyperbolic distance in the unit disc  . Conversely, from above, for a
. Conversely, from above, for a  diffeomorphism
diffeomorphism 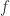 with negative schwarzian derivative,
with negative schwarzian derivative, 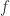 expands the hyperbolic distance in the real interval.
expands the hyperbolic distance in the real interval.
Exercise 1. “Mathematical Tools for One Dimensional Dynamics” Exercise 6.5, Chapter 6
Let 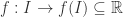 be a
be a  diffeomorphism without fixed points (
diffeomorphism without fixed points ( 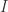 being a closed interval on the real line). If
being a closed interval on the real line). If  for all
for all 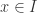 , then there exists a unique
, then there exists a unique  such that
such that  for all
for all 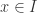 .
.
Proof. If 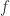 is a decreasing map, then the right boundary of the real interval I is the
is a decreasing map, then the right boundary of the real interval I is the  . Therefore, assume that
. Therefore, assume that 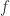 is an increasing map on the real interval I.
is an increasing map on the real interval I.
Since  has no fixed points on the real interval I, then
has no fixed points on the real interval I, then  or
or 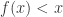 for all
for all 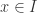 . Without lost of generality, assume
. Without lost of generality, assume  for all
for all 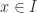 . Since
. Since 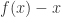 is a continuous function on the closed interval I, there exists
is a continuous function on the closed interval I, there exists  such that
such that  for all
for all 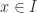 .
.
By contradiction, there exist two distinct points 
 such that
such that  and
and  for all
for all 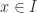 . From here, we know that
. From here, we know that 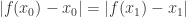 .
.
From Langrange’s mean value theorem, there exists  such that
such that  . Since the schwarzian derivative of
. Since the schwarzian derivative of 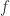 is negative, from the minimal principle, we get
is negative, from the minimal principle, we get

i.e.  . However, from the definition of
. However, from the definition of  and
and  , we get
, we get


This is a contradiction. Therefore, the existence of  is unique.
is unique.
Assume 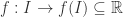 is a
is a  diffeomorphism, define the non-linearity of
diffeomorphism, define the non-linearity of 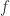 as
as

Proposition 4. 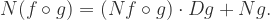
Proposition 5. 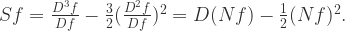
Theorem 5. Koebe Non-linearity Principle.
Given 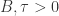 , there exists
, there exists  such that, if
such that, if ![f: [-\tau, 1+\tau] \rightarrow \mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A+%5B-%5Ctau%2C+1%2B%5Ctau%5D+%5Crightarrow+%5Cmathbb%7BR%7D&bg=ffffff&fg=2b2b2b&s=0&c=20201002) is a
is a  diffeomorphism into the reals and
diffeomorphism into the reals and  for all
for all ![t\in [-\tau,1+\tau],](https://s0.wp.com/latex.php?latex=t%5Cin+%5B-%5Ctau%2C1%2B%5Ctau%5D%2C&bg=ffffff&fg=2b2b2b&s=0&c=20201002) then we have
then we have
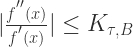
for all 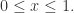 Show that
Show that 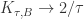 as
as 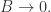 (This recovers the classical Koebe non-linearity principle).
(This recovers the classical Koebe non-linearity principle).
is the unit disc on the complex plane
is the upper half plane on the complex plane,
is the band between
and
.
is defined as
for all
is a conformal mapping, where
, then we can also define the hyperbolic metric on the domain U,
for all
is a conformal mapping which maps the upper half plane
onto the unit disc
From above formula, we can calculate the hyperbolic metric on
is
for all
is
for all
, if the interval
, then the restriction of the hyperbolic metric on the unit disc
is
for all
. Since there exists a linear map
which maps a to -1 and b to 1, i.e.
. Its derivative is
. Therefore, the hyperbolic metric on the interval I is
for all
, then the hyperbolic distance between c and d is
. Therefore, the hyperbolic distance between c and d in the interval (a,b) equals to
be a
positive function on an open subset
. Then the curvature of the metric
is given by
is the Laplacian operator
, the upper half plane
and the band
is -1.
is a conformal mapping, where
is an open subset of the complex plane
. From above, the hyperbolic metric on U is
for all
is
.
, the sphere metric on
is defined as
for all
