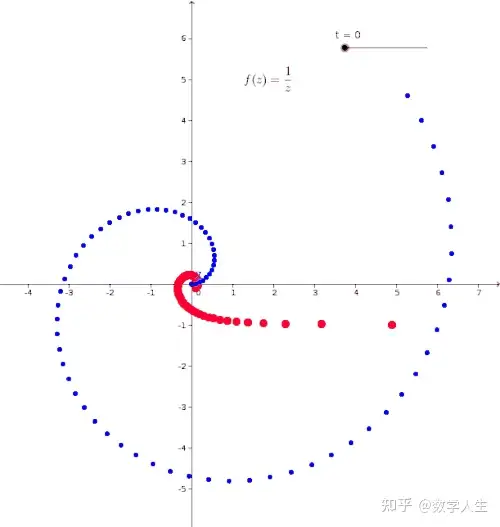
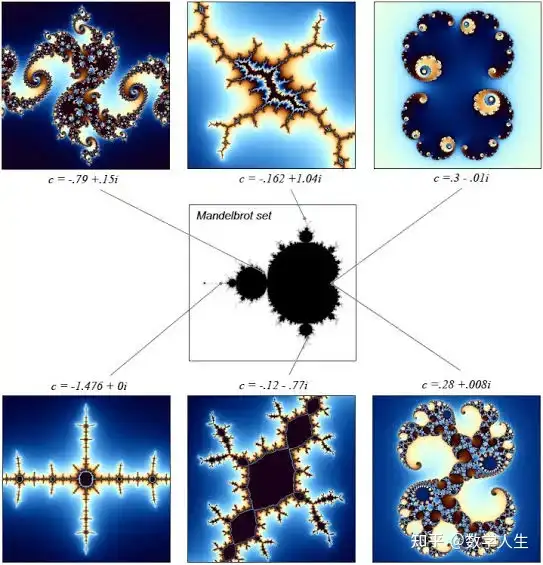
Reference Book: Joel L.Schiff- Normal Families
Some Classical Theorems
Weierstrass Theorem Let 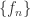 be a sequence of analytic functions on a domain
be a sequence of analytic functions on a domain  which converges uniformly on compact subsets of
which converges uniformly on compact subsets of  to a function
to a function 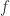 . Then
. Then 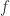 is analytic in
is analytic in  , and the sequence of derivatives
, and the sequence of derivatives  converges uniformly on compact subsets to
converges uniformly on compact subsets to  .
.
Hurwitz Theorem Let 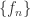 be a sequence of analytic functions on a domain
be a sequence of analytic functions on a domain  which converges uniformly on compact subsets of
which converges uniformly on compact subsets of  to a non-constant analytic function
to a non-constant analytic function  . If
. If  for some
for some 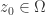 , then for each
, then for each  sufficiently small, there exists an
sufficiently small, there exists an  , such that for all
, such that for all  ,
,  has the same number of zeros in
has the same number of zeros in 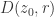 as does
as does  . (The zeros are counted according to multiplicity).
. (The zeros are counted according to multiplicity).
The Maximum Principle If  is analytic and non-constant in a region
is analytic and non-constant in a region  , then its absolute value
, then its absolute value  has no maximum in
has no maximum in  .
.
The Maximum Principle’ If  is defined and continuous on a closed bounded set
is defined and continuous on a closed bounded set 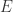 and analytic on the interior of
and analytic on the interior of 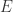 , then the maximum of
, then the maximum of  on
on 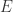 is assumed on the boundary of
is assumed on the boundary of 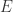 .
.
Corollary 1.4.1 If 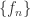 is a sequence of univalent analytic functions in a domain
is a sequence of univalent analytic functions in a domain  which converge uniformly on compact subsets of
which converge uniformly on compact subsets of  to a non-constant analytic function
to a non-constant analytic function 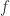 , then
, then 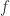 is univalent in
is univalent in  .
.
Definition 1.5.1 A family of functions  is locally bounded on a domain
is locally bounded on a domain  if, for each
if, for each  , there is a positive number
, there is a positive number  and a neighbourhood
and a neighbourhood  such that
such that  for all
for all  and all
and all  .
.
Theorem 1.5.2 If  is a family of locally bounded analytic functions on a domain
is a family of locally bounded analytic functions on a domain  , then the family of derivatives
, then the family of derivatives  form a locally bounded family in
form a locally bounded family in  .
.
The converse of Theorem 1.5.2 is false, since  . However, the following partial converse does hold.
. However, the following partial converse does hold.
Theorem 1.5.3 Let  be a family of analytic functions on
be a family of analytic functions on  such that the family of derivatives
such that the family of derivatives 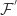 is locally bounded and suppose that there is some
is locally bounded and suppose that there is some  with
with  for all
for all  . Then
. Then  is locally bounded. (Hint: find a path connecting
is locally bounded. (Hint: find a path connecting  and
and  .)
.)
Definition 1.6.1 A family  of functions defined on a domain
of functions defined on a domain  is said to be equicontinuous (spherically continuous) at a point
is said to be equicontinuous (spherically continuous) at a point  if, for each
if, for each  , there is a
, there is a  such that
such that 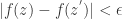 ,
,  whenever
whenever  , for every
, for every  . Moreover,
. Moreover,  is equicontinuous (spherical continuous) on a subset
is equicontinuous (spherical continuous) on a subset 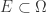 if it is continuous (spherically continuous) at each point of
if it is continuous (spherically continuous) at each point of 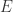 .
.
Normal Families of Analytic Functions
Definition 2.1.1 A familiy  of analytic functions on a domain
of analytic functions on a domain  is normal in
is normal in  if every sequence of functions
if every sequence of functions  contains either a subsequence which converges to a limit function
contains either a subsequence which converges to a limit function  uniformly on each compact subset of
uniformly on each compact subset of  , or a subsequence which converges uniformly to
, or a subsequence which converges uniformly to  on each compact subset.
on each compact subset.
The family  is said to be normal at a point
is said to be normal at a point 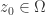 if it is normal in some neighbourhood of
if it is normal in some neighbourhood of  .
.
Theorem 2.1.2 A family of analytic functions  is normal in a domain
is normal in a domain  if and only if
if and only if  is normal at each point in
is normal at each point in  .
.
Theorem 2.2.1 Arzela-Ascoli Theorem. If a sequence  of continuous functions converges uniformly on a compact set
of continuous functions converges uniformly on a compact set 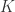 to a limit function
to a limit function  , then
, then  is equicontinuous on
is equicontinuous on 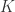 , and
, and 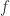 is continuous. Conversely, if
is continuous. Conversely, if  is equicontinuous and locally bounded on
is equicontinuous and locally bounded on  , then a subsequence can be extracted from
, then a subsequence can be extracted from  which converges locally uniformly in
which converges locally uniformly in  to a (continuous) limit function
to a (continuous) limit function 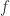 .
.
Montel’s Theorem If  is a locally bounded family of analytic functions on a domain
is a locally bounded family of analytic functions on a domain  , then
, then  is a normal family in
is a normal family in  .
.
Koebe Distortion Theorem Let  be analytic univalent in a domain
be analytic univalent in a domain  and
and 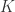 a compact subset of
a compact subset of  . Then there exists a constant
. Then there exists a constant 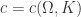 such that for any
such that for any  ,
,  .
.
Vitali-Porter Theorem Let  be a locally bounded sequence of analytic functions in a domain
be a locally bounded sequence of analytic functions in a domain  such that
such that  exists for each
exists for each  belonging to a set
belonging to a set 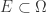 which has an accumulation point in
which has an accumulation point in  . Then
. Then 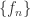 converges uniformly on compact subsets of
converges uniformly on compact subsets of  to an analytic function.
to an analytic function.
Proof. From Montel’s Theorem, 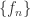 is normal, extract a subsequence
is normal, extract a subsequence 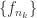 which converges normally to an analytic function
which converges normally to an analytic function 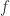 . Then
. Then  for each
for each  . Suppose, however, that
. Suppose, however, that 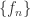 does not converge uniformly on compact subsets of
does not converge uniformly on compact subsets of  to
to 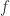 . Then there exists some
. Then there exists some  , a compact subset
, a compact subset  , as well as a subsequence
, as well as a subsequence  and points
and points 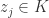 satisfying
satisfying 
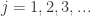 . Now
. Now  itself has a subsequence which converges uniformly on compact subsets to an analytic function
itself has a subsequence which converges uniformly on compact subsets to an analytic function 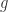 , and
, and  from above. However, since
from above. However, since 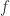 and
and 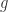 must agree at all points of
must agree at all points of 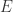 , the Identity Theorem for analytic functions implies
, the Identity Theorem for analytic functions implies  on
on  , a contradiction which establishes the theorem.
, a contradiction which establishes the theorem.
Fundamental Normality Test Let  be the family of analytic functions on a domain
be the family of analytic functions on a domain  which omit two fixed values
which omit two fixed values  and
and 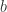 in
in 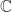 . Then
. Then  is normal in
is normal in  .
.
Generalized Normality Test Suppose that  is a family of analytic functions in a domain
is a family of analytic functions in a domain  which omit a value
which omit a value 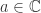 and such that no function of
and such that no function of  assumes the value
assumes the value  at more that
at more that 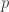 points. Then
points. Then  is normal in
is normal in  .
.
2.3 Examples:
Assume 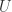 is the unit disk in the complex plane,
is the unit disk in the complex plane,  is a region (connected open set) in
is a region (connected open set) in 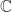 .
.
1.  in
in 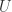 . Then
. Then  is normal in
is normal in 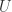 , but not compact since
, but not compact since  . In the domain
. In the domain  ,
,  is normal.
is normal.
2.  is a normal family in
is a normal family in  but not compact.
but not compact.
3.  analytic in
analytic in  and
and  . Then
. Then  is normal in
is normal in  and compact.
and compact.
4.  analytic in
analytic in  and
and 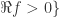 . Then
. Then  is normal but not compact. Hint:
is normal but not compact. Hint: 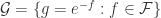 is a uniformly bounded family.
is a uniformly bounded family.
5. 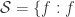 analytic, univalent in
analytic, univalent in 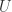 ,
, 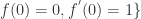 . These are the normalised “Schlicht” functions in
. These are the normalised “Schlicht” functions in 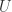 .
. 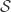 is normal and compact.
is normal and compact.
Normal Families of Meromorphic Functions
Assume a function  is analytic in a neighbourhood of
is analytic in a neighbourhood of  , except perhaps at
, except perhaps at  itself. In other words,
itself. In other words,  shall be analytic in a region
shall be analytic in a region 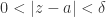 . The point
. The point  is called an isolated singularity of
is called an isolated singularity of  . There are three cases about an isolated singularity. The first one is a removable singularity, the second one is a pole, the third one is an essential singularity. A function
. There are three cases about an isolated singularity. The first one is a removable singularity, the second one is a pole, the third one is an essential singularity. A function  which is analytic in a region
which is analytic in a region  , except for poles, is said to be meromorphic in
, except for poles, is said to be meromorphic in  .
.
The chordal distance 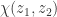 between
between  and
and  is
is
 if
if  and
and  are in the finite plane, and
are in the finite plane, and
 if
if 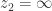 . Clearly,
. Clearly,  , and
, and 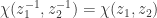 . The chordal metric and spherical metric are uniformly equivalent and generate the same open sets on the Riemann sphere.
. The chordal metric and spherical metric are uniformly equivalent and generate the same open sets on the Riemann sphere.
Definition 1.2.1 A sequence of functions 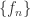 converges spherically uniformly to
converges spherically uniformly to 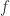 on a set
on a set  if, for any
if, for any  , there is a number
, there is a number  such that
such that  implies
implies 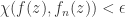 , for all
, for all  .
.
Definition 3.1.1 A family  of meromorphic functions in a domain
of meromorphic functions in a domain  is normal in
is normal in  if every sequence
if every sequence 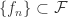 contains a subsequence which converges spherically uniformly on compact subsets of
contains a subsequence which converges spherically uniformly on compact subsets of  .
.
Theorem 3.1.3 Let 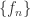 be a sequence of meromorphic functions on a domain
be a sequence of meromorphic functions on a domain  . Then
. Then 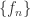 converges spherically uniformly on compact subsets of
converges spherically uniformly on compact subsets of  to
to 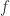 if and only if about each point
if and only if about each point  there is a closed disk
there is a closed disk  in which
in which  or
or  uniformly as
uniformly as 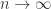 .
.
Corollary 3.1.4 Let 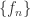 be a sequence of meromorphic functions on
be a sequence of meromorphic functions on  which converges spherically uniformly on compact subsets to
which converges spherically uniformly on compact subsets to 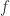 . Then
. Then 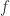 is either a meromorphic function on
is either a meromorphic function on  or identically equal to
or identically equal to  .
.
Corollary 3.1.5 Let 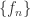 be a sequence of analytic functions on a domain
be a sequence of analytic functions on a domain  which converge spherically uniformly on compact subsets of
which converge spherically uniformly on compact subsets of  to
to 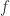 . Then
. Then 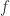 is either analytic on
is either analytic on  or identically equal to
or identically equal to  .
.
Theorem 3.2.1 A family  of meromorphic functions in a domain
of meromorphic functions in a domain  is normal if and only if
is normal if and only if  is spherically equicontinuous in
is spherically equicontinuous in  .
.
Fundamental Normality Test Let  be a family of meromorphic functions on a domain
be a family of meromorphic functions on a domain  which omit three distinct values
which omit three distinct values 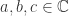 . Then
. Then  is normal in
is normal in  .
.
Vitali-Porter Theorem Let  be a sequence belonging to a spherically equicontinuous family of meromorphic functions such that
be a sequence belonging to a spherically equicontinuous family of meromorphic functions such that  converges spherically on a point set
converges spherically on a point set 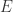 having an accumulation point in
having an accumulation point in  . Then
. Then 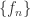 converges spherically uniformly on compact subsets of
converges spherically uniformly on compact subsets of  .
.
Let  be meromorphic on a domain
be meromorphic on a domain  . If
. If 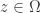 is not a pole, the derivative in the spherical metric, called the spherical derivative, is given by
is not a pole, the derivative in the spherical metric, called the spherical derivative, is given by 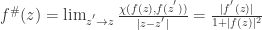 . If
. If  is a pole of
is a pole of  , define
, define  .
.
Marty’s Theorem A family  of meromorphic functions on a domain
of meromorphic functions on a domain  is normal if and only if for each compact subset
is normal if and only if for each compact subset  , there exists a constant
, there exists a constant  such that spherical derivative
such that spherical derivative  that is,
that is,  is locally bounded.
is locally bounded.