Thurston 生平介绍
早年生活与教育
威廉·瑟斯顿于1946年10月30日出生于美国华盛顿特区,父亲保罗·瑟斯顿是航空工程师,母亲玛格丽特是裁缝。幼年因先天性斜视导致深度知觉障碍,母亲通过训练帮助他重建三维视觉能力。1967年,他作为首届学生从新佛罗里达学院毕业,本科论文为拓扑学构建直觉主义基础。1972年在加州大学伯克利分校师从莫里斯·赫希(Morris Hirsch)获得博士学位,论文题为《圆丛的三维流形叶状结构》。

学术生涯
瑟斯顿的职业生涯始于普林斯顿高等研究院(1972-1973)和麻省理工学院(1973-1974)。1974年,28岁的他成为普林斯顿大学正教授,展现了非凡的学术潜力。1991年重返伯克利任教授(1991-1996),并担任数学科学研究所(MSRI)所长(1992-1997)。1996年转至加州大学戴维斯分校,2003年加入康奈尔大学直至去世。他是最早将计算机引入纯数学研究的学者之一,曾启发杰弗里·威克斯开发三维双曲空间计算程序SnapPea。

研究贡献
瑟斯顿以低维拓扑学的革命性工作闻名:
- 叶状结构理论(1970年代早期):解决了流形上Haefliger结构的可积性问题,构造了三维球面上具有连续变化Godbillon-Vey不变量的叶状结构族。
- 几何化猜想(1976年后):提出三维流形的几何分类框架(含8种Thurston几何),证明双曲德恩手术定理和哈肯流形的双曲化定理,为佩雷尔曼最终证明庞加莱猜想奠定基础。
- 密度猜想(与Dennis Sullivan合作):推广了Klein群极限的代数性质,2011-2012年被完全证明。
- 轨道折叠定理(1981年):将几何化理论扩展至三维轨道空间,2000年左右由多团队完成证明。
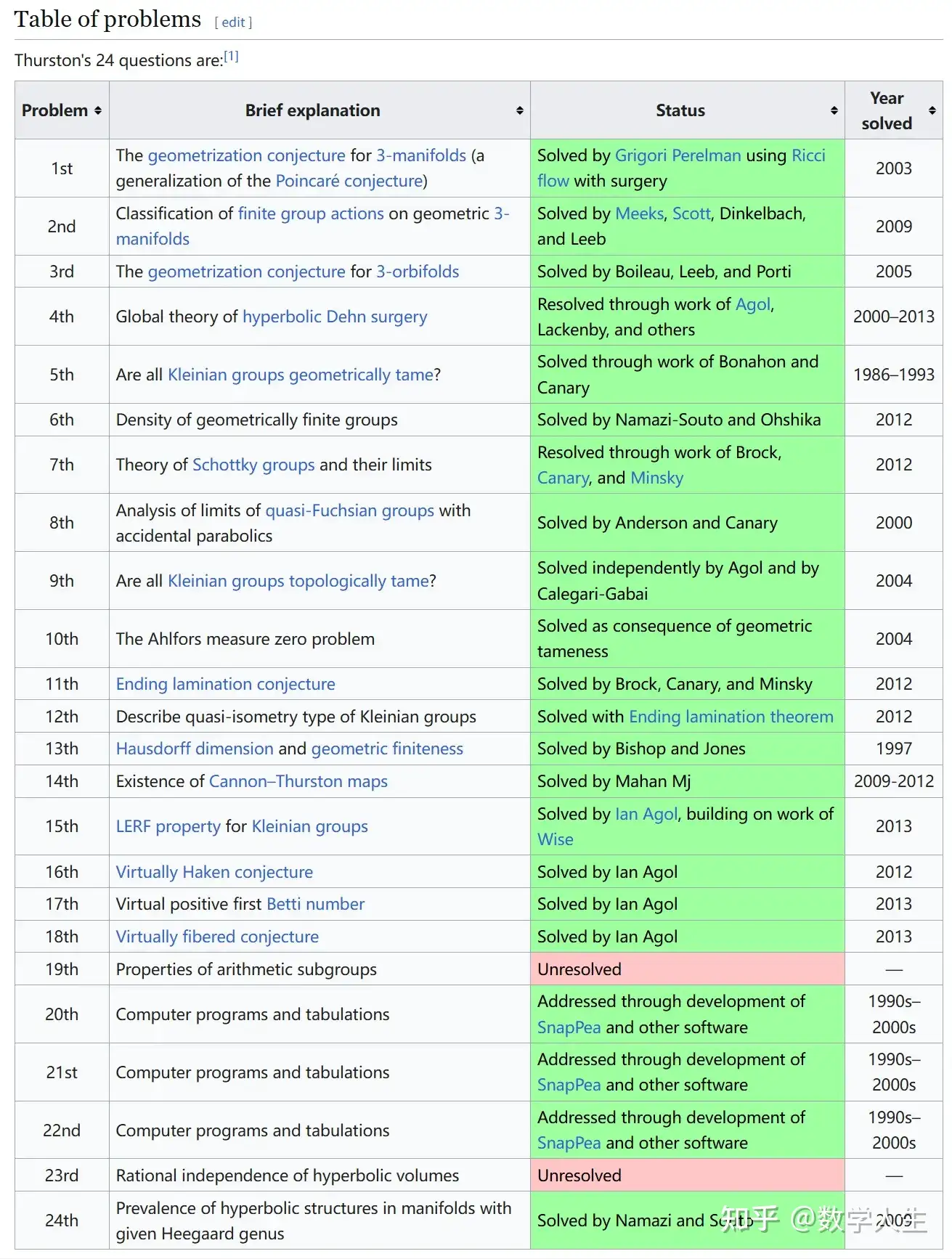
荣誉与奖项
菲尔兹奖(1982年):表彰其对2-3维拓扑学的变革性贡献。
奥斯瓦尔德·维布伦几何奖(1976年,与James Simons共享)。
美国数学会首届图书奖(2005年,《三维几何与拓扑》)。
斯蒂尔奖(2012年):因其工作“彻底改变了三维流形理论”。


个人生活
瑟斯顿与第一任妻子Rachel Findley育有三子,其中长子Dylan成为印第安纳大学数学家。与第二任妻子Julian Muriel Thurston育有两子女。2011年确诊鼻窦黏膜黑色素瘤,于2012年8月21日在纽约罗切斯特去世,享年65岁。
学术遗产
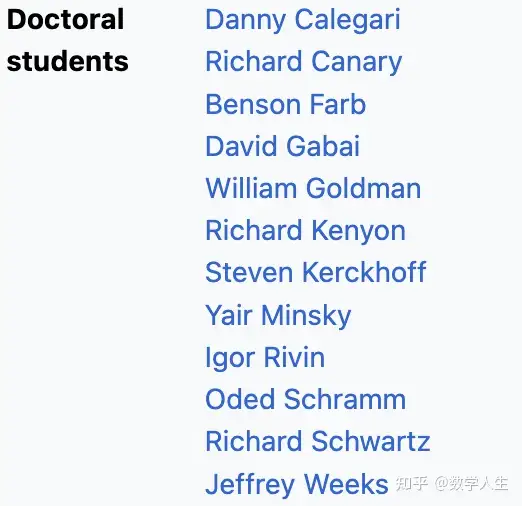
瑟斯顿培养了包括David Gabai、William Goldman、Oded Schramm 等杰出学生。他的思想深刻影响了几何拓扑学,尤其是双曲几何在低维流形中的应用。其著作《三维几何与拓扑》等成为经典教材。康奈尔大学称他为“数学界的真正先驱”。
《On Proof and Progress in Mathematics》
William P. Thurston 在《On Proof and Progress in Mathematics》(1994)这篇经典论文中,Thurston超越了传统数学哲学的讨论,深入探讨了数学研究的本质、数学理解的多样性以及数学知识的社会化过程。数学常被视为一门纯粹的逻辑科学,其发展往往被简化为“定义—定理—证明”(DTP)的机械过程。然而,数学家的工作远不止于此。他们不仅是形式体系的构建者,更是人类认知的探索者、思想的传播者,以及数学知识社会化网络的维护者。William Thurston 在本文中深刻剖析了数学家的多重角色,揭示了数学研究的本质及其对人类思维发展的重要意义。

1. 数学家的创造性角色:超越形式化框架
传统的 DTP 模型将数学研究简化为从公理出发的演绎推理,但它无法解释数学问题的来源。数学家的工作并非仅仅是生产定理和证明,而是通过猜想、启发式论证和直觉洞察推动数学的发展。正如 Thurston 所言,数学的核心价值在于“帮助人们更清晰、更有效地思考数学”,而不仅仅是积累形式化的结论。
Jaffe 和 Quinn 提出的“推测性数学”(speculative mathematics)补充了 DTP 模型的不足,强调数学家需要通过提出猜想、探索可能性来推动学科进步。然而,Thurston 进一步指出,数学的真正挑战在于如何保持原始数学洞察的丰富性,而不是让形式化定义掩盖其背后的思维多样性。

2. 数学家的认知贡献:多元理解与思维整合

数学理解并非单一的逻辑过程,而是多维度、个体化的认知活动。Thurston 以“导数”为例,列举了七种不同的理解方式:
无穷小量(微积分早期思想)
符号运算(代数规则)
逻辑定义(ε-δ 语言)
几何直观(切线斜率)
物理速率(瞬时速度)
线性逼近(最佳局部近似)
显微极限(高倍放大下的极限行为)
这些理解方式并非互相排斥,而是互补共存。数学家的工作不仅是建立严格的定义,还要调和不同视角,使数学概念在不同领域(如物理、工程、计算机科学)中都能被有效应用。Thurston 强调,数学教育的核心挑战之一就是帮助学生内化这些不同的思维方式,而不仅仅是记忆公式和证明。

3. 数学家的社会角色:知识的传播与共享
数学的发展依赖于有效的交流,而 Thurston 指出,当前的数学界过于关注前沿成果的发表,而忽视了基础认知结构的传播。他呼吁数学家应更注重“如何向未知者传达数学思想”,而不仅仅是向同行展示技术性证明。

例如,在坐标参数化的研究中,数学家需要找到一种表达方式,使得非专业人士也能理解其核心思想。这意味着数学语言必须既能精确描述问题,又能适应不同背景学习者的认知需求。Thurston 认为,数学的未来发展需要更多精力投入在数学思维的普及,而不仅仅是追逐最新的理论突破。
4. 数学证明的社会化本质:共识与动态修正
Thurston 通过自身经历揭示了数学证明的社会化特征:
共识验证:许多数学定理的接受并非仅依赖于书面证明,而是通过学术共同体的口头交流、引用和集体认可逐渐确立。
动态纠错:某些“公认”的定理可能缺乏完整证明,甚至存在错误,但数学界通过持续的讨论和修正维持其可靠性。
知识网络:数学理解不仅存在于论文中,更嵌入研究者的思维网络和社会互动中。
这一观点挑战了“数学证明是绝对真理”的传统观念,强调数学知识是动态、社会化的认知构建,而非静态的逻辑产物。

5. 数学家作为人类思维的塑造者
Thurston 的论述表明,数学家的工作远超出形式逻辑的范畴。他们是:
思想的创造者(提出猜想,探索未知结构)
认知的整合者(调和不同理解方式,促进跨学科应用)
知识的传播者(发展有效表达,使数学更易被理解)
社会共识的维护者(通过学术网络验证和修正数学真理)

数学的真正进步不仅体现在定理数量的增长,更在于人类对数学的认知深度和传播效率的提升。因此,数学家的核心使命不仅是证明,更是推动人类思维的发展。全文始终贯穿一个核心主张:数学不仅是形式系统,更是人类认知活动与社会实践的复合体,需要从思维多样性、交流有效性和知识社会化等维度重新审视数学的本质价值。
十个与 Thuston 相关的小故事

Yair Minsky的回忆:比尔的文字具有一种称之为”唯一正确补全特性”的写作风格。他的行文清晰但极为简练,初读(甚至再读)时总难以把握该如何补全论证细节。Minsky屡次经历这样的体验:苦思冥想许久后意识到某个关键论点或条件确实被遗漏了,但当Minsky重新查阅原文时,却发现那些内容自始至终都白纸黑字地写在那里。Minsky回忆Thurston的教学风格——注重几何直觉而非形式化计算。一次,Minsky在课堂上试图用公式证明某个定理时,认真研读证明过程,理解了演算步骤的脉络,回到课堂后在黑板上逐步推演。Thurston痛苦地打断他说:“我想要的不是公式……”这体现了Thurston对直观理解的执着。某年比尔与丹尼斯·沙利文将各自的研究生团队合并,在普林斯顿大学和纽约市立大学研究生中心轮流举办联合研讨会。这些研讨会及其前后、乃至火车旅途中的交谈,都让我们获益良多。
Lee Mosher的厨房时光:Mosher描述与Thurston一家在普林斯顿的“食物合作社”生活。他们一起购物、做饭,厨房常陷入混乱。Thurston的数学热情甚至延伸到生活细节,比如用UNIX工具 grep 研究群论,并兴奋地宣布“我能用这个群做计算!”。

Benson Farb的“泡泡理论”:Farb向Thurston请教负曲率流形的课题时,对方陷入两分钟的沉思后突然说:“哦,这像一堆泡泡,泡泡间的相互作用有限。”Farb一头雾水地记下“泡泡,有限作用”,三年后完成论文时发现这竟是问题的完美总结。
Danny Calegari的地板绘图:在加州大学戴维斯分校,Thurston曾兴奋地买来巨幅纸张和彩笔,与Calegari趴在地上画数学构造。他感慨:“在普林斯顿时我常这么干!”这一幕展现了Thurston用视觉化探索数学的童趣。
Ian Agol的二进制手指计数:在MSRI的野餐活动中,Thurston向学生演示如何用手指表示二进制数,并全程用这种方法数完了徒步的步数。他还用SnapPea程序颠覆了Agol对纽结理论的认知,强调“从简单模型出发”的研究哲学。
Carol Wood的MSRI改革:担任MSRI所长期间,Thurston推动“数学对话”打破研究者与教师壁垒,引入3D打印等新技术,甚至试图将机构昵称从“misery”(痛苦)改为“emissary”(使者)。他办公桌上总摆着自制的猪与人类DNA胶带模型,向来访者展示科学之趣。

Tan Lei的跨领域顿悟:2011年,Thurston在研究三次多项式迭代时,突然发现其组合结构与S^3中的判别式补集存在隐藏联系。经过一周沉思,他构建出两者间的桥梁,并激动地宣布:“这适用于任意次数!”展现了他“数学万物互联”的信念。
幼儿园的镜面实验:在解释“轨形空间”时,Thurston带着两面镜子和蓝精灵玩偶去幼儿园课堂。孩子们通过调整镜面角度,直观理解了多重镜像如何生成无限宇宙,体现了他用生活化方式传达深奥概念的才能。

脑模型趣事:参与创造力研究后,Thurston收到黏土制作的脑模型。他逢人便炫耀,甚至在某次数学讨论中突然插话:“我的大脑明天就到!”让在场学者陷入迷惑,直到他掏出那个粉色模型。

临终前的数学热情:2011年Banff会议上,重病中的Thurston仍积极参与Dani Wise的讲座,甚至开玩笑问:“如果我给你1000美元找论证错误,你会检查哪里?”直至生命最后,他仍通过Dropbox与全球年轻数学家合作,延续着思想的激荡。