问题：他到底是一个人，还是一个研究所？

从数学家们的评价来看，柯尔莫哥洛夫的研究广度和深度远超单个学者的极限。他不仅独自建立了概率论、算法复杂性、湍流理论等多个领域的数学基础，还培养了一代顶尖学者。因此，他既是天才的个人，也是一个“行走的数学研究所”——他的影响力至今仍在塑造现代数学和科学。在1963年，美国统计学家沃尔夫·维茨惊叹：“我想知道，柯尔莫戈洛夫到底是一个人呢，还是一个研究机构？”

个人经历

安德烈·尼古拉耶维奇·柯尔莫哥洛夫（Andrei Nikolaevich Kolmogorov，1903-1987）是20世纪最伟大的数学家之一，被誉为“数学的巨人”。他出生于俄罗斯坦波夫，母亲在分娩时去世，父亲因参与革命活动被流放并在1919年内战中去世。柯尔莫哥洛夫由母亲的姐姐维拉·雅科夫列夫娜抚养长大，并在雅罗斯拉夫尔附近的家族庄园中度过童年。他自幼展现出非凡的数学天赋，5岁时就独立发现了奇数求和与平方数的关系（1=1²，1+3=2²等），并在家庭自办的杂志《春燕》中发表数学问题。

柯尔莫哥洛夫早年兴趣广泛，涉猎生物学、历史、文学和音乐。1920年进入莫斯科国立大学后，他师从著名数学家尼古拉·卢津（Nikolai Luzin），并在本科期间就发表了关于傅里叶级数发散性的突破性成果（1922年）。1925年毕业后，他与亚历山大·辛钦（Aleksandr Khinchin）合作研究概率论，开启了其辉煌的学术生涯。1931年，他成为莫斯科大学教授，并与好友帕维尔·亚历山德罗夫（Pavel Alexandrov）共同建立了深厚的学术与个人友谊。

柯尔莫哥洛夫最著名的贡献是1933年出版的《概率论基础》（Grundbegriffe der Wahrscheinlichkeitsrechnung），其中提出了概率论的公理化体系，彻底解决了希尔伯特第六问题中“物理学的公理化”部分。他还创立了KAM理论（与Arnold和Moser合作）、柯尔莫哥洛夫复杂性理论，并在湍流理论、拓扑学、信息论等领域作出开创性工作。尽管在斯大林时期面临政治压力，他仍获得斯大林奖（1941年）和列宁勋章等荣誉。

柯尔莫哥洛夫终身致力于教育，创办了莫斯科物理数学寄宿学校（后以他命名），并亲自编写教材。他晚年研究算法信息论，提出“概率论应基于信息论而非相反”的颠覆性观点。1987年因帕金森病逝世于莫斯科，其思想至今仍深刻影响着数学与科学领域。

数学成就

柯尔莫哥洛夫是20世纪最具影响力的数学家之一，他的研究横跨多个数学领域，包括概率论、拓扑学、信息论、算法复杂性、动力系统、流体力学等。他的工作不仅奠定了现代数学的多个分支，而且对物理学、计算机科学和统计学产生了深远影响。以下是他在不同领域的重大贡献：

1. 概率论的公理化（1933）

柯尔莫哥洛夫最著名的贡献是1933年出版的《概率论基础》（Grundbegriffe der Wahrscheinlichkeitsrechnung），其中他基于测度论建立了概率论的公理化体系。这一工作解决了希尔伯特第六问题（“物理学的公理化”）的一部分，并彻底改变了概率论的研究方式。 柯尔莫哥洛夫公理：他定义了概率空间，其中： 是样本空间， 是事件， -代数， 是概率测度这些公理至今仍是概率论的标准框架。条件期望：他严格定义了条件期望，使其成为现代概率论的核心工具。零一律（Kolmogorov’s Zero-One Law）：证明某些极限事件的概率只能是0或1，这对随机过程的研究至关重要。

2. 随机过程与马尔可夫链

柯尔莫哥洛夫在随机过程领域做出了奠基性工作：柯尔莫哥洛夫方程（Chapman-Kolmogorov方程）：描述马尔可夫过程的转移概率演化，是随机过程理论的核心工具。扩散过程：他研究了连续时间随机过程的微分方程，为现代金融数学和物理学中的随机微分方程（SDE）奠定了基础。大数定律的推广：他给出了独立随机变量序列满足强大数定律的充要条件。

3. 算法信息论与柯尔莫哥洛夫复杂性（1960s）

柯尔莫哥洛夫在1960年代提出了算法复杂性的概念，后来被称为柯尔莫哥洛夫复杂性（Kolmogorov Complexity），这是信息论和计算理论的重要突破：定义：一个字符串的柯尔莫哥洛夫复杂性是最短程序（在某种通用计算机上）能生成该字符串的长度。随机性：如果一个字符串的柯尔莫哥洛夫复杂性接近其自身长度，则该字符串是“随机”的。影响：这一理论影响了数据压缩、密码学、机器学习等领域，并与所罗门诺夫（Solomonoff）和柴廷（Chaitin）的工作共同构成了算法信息论的基础。

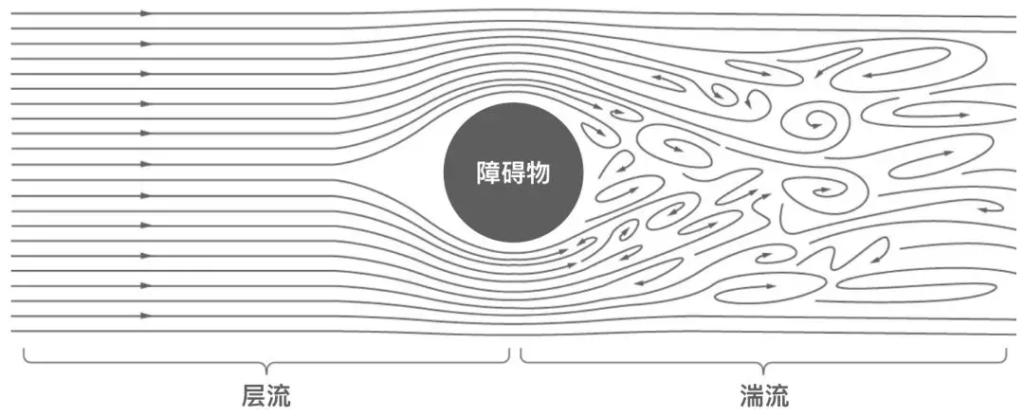
4. 湍流理论与Kolmogorov-Obukhov定律（1941）

柯尔莫哥洛夫在流体力学中提出了湍流能谱的标度律（Kolmogorov-Obukhov定律）：-5/3定律：在惯性子区，湍流能量谱

，

这一理论至今仍是湍流研究的基础。Kolmogorov尺度：定义了湍流的最小尺度（Kolmogorov微尺度），影响气象学、海洋学和工程学。

5. 拓扑学与同调论（1930s）

柯尔莫哥洛夫在代数拓扑领域也有重要贡献：上同调环（Cohomology Ring）：与亚历山大（J.W. Alexander）独立发现，是现代代数拓扑的核心工具。Kolmogorov空间（空间）：定义了最弱的分离公理，影响了一般拓扑学的发展。维数理论：他研究了拓扑空间的维数，并构造了开映射增加维数的反例，挑战了当时对维数的直观理解。

6. 动力系统与KAM理论（1954）

柯尔莫哥洛夫在哈密顿系统的研究中提出了KAM理论（Kolmogorov-Arnold-Moser理论）：稳定性问题证明在微扰下，某些可积系统的不变环面仍然存在，解决了太阳系稳定性等经典力学问题。KAM理论为混沌动力学奠定了基础，影响天体力学和统计物理。

7. 统计学与柯尔莫哥洛夫-斯米尔诺夫检验（1933）

柯尔莫哥洛夫在数理统计中提出了柯尔莫哥洛夫-斯米尔诺夫检验（K-S检验）：非参数检验用于判断样本是否来自某一特定分布，广泛应用于数据分析，他的工作推动了非参数统计的发展。

8. 信息论与熵（1950s）

柯尔莫哥洛夫与辛钦（Khinchin）和香农（Shannon）共同推动了信息论的发展：柯尔莫哥洛夫熵用于度量动力系统的混沌程度，影响遍历理论和复杂性科学。信息几何他的工作为信息几何（Information Geometry）提供了数学基础。

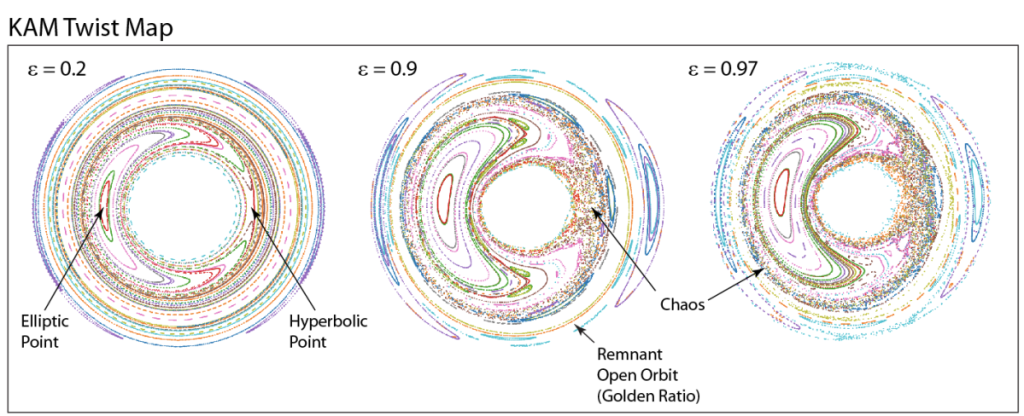
KAM 理论

KAM理论（Kolmogorov-Arnold-Moser理论）是动力系统理论中关于哈密顿系统稳定性的重要成果，由三位数学家Kolmogorov（1954）、Arnold（1960年代）和Moser（1960年代）逐步完善。该理论起源于对经典力学中可积系统受扰动后行为的研究，旨在解决“小分母问题”和长期稳定性难题。其核心结论是：在满足非退化性条件（如Hessian矩阵非奇异）和Diophantine频率条件（频率向量满足无理比例且难以被有理数逼近）的前提下，弱扰动下多数不变环面（KAM环面）会以微小形变的形式保留，而非完全破坏。

由来与历史背景

经典问题：Poincaré在研究三体问题时发现，可积系统的扰动可能导致共振和轨道不稳定，但严格证明长期稳定性极为困难。Kolmogorov突破（1954）：提出不变环面在扰动下持续存在的思想，并引入牛顿迭代法解决收敛性问题。Arnold与Moser的推广：Arnold将理论扩展到多自由度哈密顿系统，Moser则放宽了光滑性要求，适用于有限次可微系统（如类）。

核心内容

1. 非退化条件：要求未扰动系统的频率随作用量变化（如，确保系统非线性。

2. 频率条件：频率比需满足（, ），排除共振。

3. 结论：扰动后，多数环面（测度趋近于全集）保持拟周期运动，其余部分形成“随机层”或混沌带。

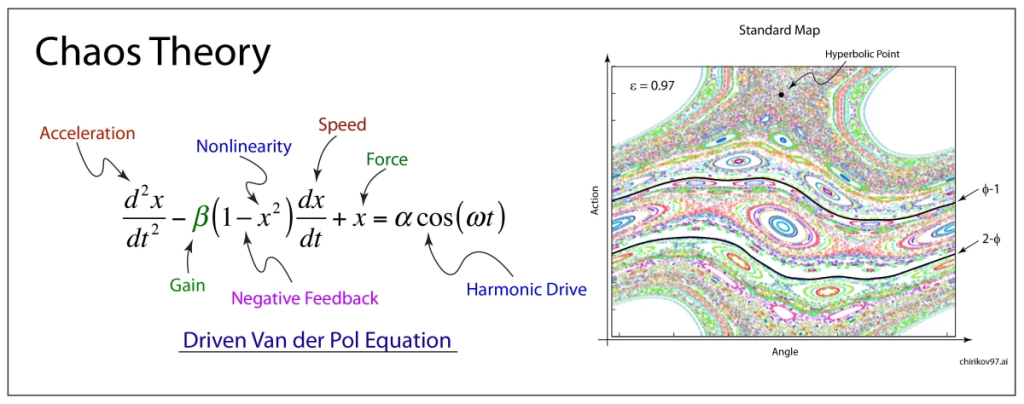
应用场景包括但不限于天体力学（解释太阳系长期稳定性（如木星轨道的KAM环面阻止混沌扩散））、等离子体物理（约束磁场中粒子运动的环面结构）、非线性动力学（研究标准映射（Standard Map）中规则岛与混沌区的分界）、统计力学（反驳“遍历性普遍成立”的假设，证明弱耦合多振子系统可能存在能非均分）。

局限性

1. 小扰动限制：仅适用于，实际物理系统可能超出此范围。

2. 高维扩散：在自由度时，Arnold扩散表明非KAM环面区域可能存在缓慢混沌输运。

3. 非光滑系统：Moser版本虽放宽条件，但仍需一定光滑性，不适用于不连续扰动（如碰撞系统）。

KAM理论揭示了规则运动与混沌的微妙共存，成为连接可积系统与遍历理论的桥梁，其思想也被拓展至非哈密顿系统（如保体积映射）和无限维系统（如某些偏微分方程）。

其他数学家的评价

要想赢得足球名宿的认可，难度堪比在世界杯决赛加时赛中完成一记倒挂金钩破门——这些见多识广的老江湖见识过马拉多纳的连过五人、齐达内的天外飞仙，他们的标准早已被传奇拔高到云层之上。就像贝肯鲍尔不会轻易称赞后卫的铲断，克鲁伊夫很少夸奖前锋的跑位，除非你的表现能让他们想起自己当年的神迹，或是展现出超越时代的灵光。毕竟，这些亲手书写过足球历史的人，眼光里永远带着黄金年代的滤镜。要想赢得菲尔兹奖或沃尔夫奖得主的赞许，难度堪比在数学的宇宙中徒手构造一个非交换的完美晶体——这些思维已触及人类智力巅峰的巨人，见识过格罗滕迪克的概形之海，领略过外尔的对称性之舞，他们的标准早已被黎曼、庞加莱等传奇铸就成了不可撼动的丰碑。就像塞尔不会轻易称赞一个同调论的构造，陶哲轩很少夸奖某个解析数论的技巧，除非你的工作能让他们想起高斯式的思想飞跃。毕竟，这些亲手拓展过数学边界的人，评判时总带着对”数学之美”近乎苛刻的直觉——那是唯有在代数与几何的深渊中潜游过千百回的灵魂才能拥有的嗅觉。下面，我们来看一下其他数学家对柯尔莫哥洛夫的评价。

P. S. Aleksandrov（帕维尔·亚历山德罗夫）亚历山德罗夫称柯尔莫哥洛夫为“数学王子”，强调其思想的广度和深度在同时代数学家中无与伦比。他指出柯尔莫哥洛夫的研究覆盖了从概率论到拓扑学等二十多个数学领域，且在每个领域都带来了根本性的革新（《The Life and Work of Kolmogorov》）。在柯尔莫哥洛夫50岁生日时，亚历山德罗夫还提到：“他的任何一篇论文都能引发对整个领域的重新评估。”

A. Ya. Khinchin（亚历山大·辛钦）辛钦认为柯尔莫哥洛夫具有罕见的才能，能将高度抽象的数学与实际问题结合。他特别指出：“柯尔莫哥洛夫最引人注目的特质是其思想的丰富性——他关于任何工作的每一句话都可能成为一篇博士论文的基础。”（《The Life and Work of Kolmogorov》）。

I. M. Gelfand（伊斯雷尔·盖尔范德）盖尔范德评价道：“数学被视为一门统一学科，很大程度上归功于柯尔莫哥洛夫。”他强调了柯尔莫哥洛夫在整合数学不同分支中的核心作用（《The Life and Work of Kolmogorov》）。

V. I. Arnold（弗拉基米尔·阿诺尔德） 阿诺尔德将柯尔莫哥洛夫与庞加莱、高斯、欧拉和牛顿并列，称“仅需五代人（柯尔莫哥洛夫-庞加莱-高斯-欧拉-牛顿）就能将我们与科学的源头连接起来”。他还提到柯尔莫哥洛夫对莫斯科大学数学系的深远影响，称其与佩特罗夫斯基共同塑造了该系的黄金时代（《A few words on Andrei Nikolaevich Kolmogorov》）。

N. H. Bingham 指出，柯尔莫哥洛夫1933年的《概率论基础》为概率论的公理化奠定了基础，解决了希尔伯特第六问题中关于概率论公理化的部分，甚至影响了保罗·莱维等学者（《Andrey Kolmogorov – MacTutor History of Mathematics》）。

Benoit Mandelbrot 在湍流研究中引用柯尔莫哥洛夫1941年的理论，认为其开创性地解释了能量级联现象，尽管后续发现需通过分形理论修正“间歇性”问题（《Fractals: A Very Short Introduction》）。

柯尔莫哥洛夫被广泛视为20世纪最具原创性和影响力的数学家之一，其工作不仅重塑了多个数学领域，还通过教育和跨学科研究留下了持久遗产。笔者貌似找到一个 Andrei Kolmogorov 不研究的领域，那就是数论（Number Theory）。

总结

柯尔莫哥洛夫的数学贡献几乎覆盖了现代数学的所有核心领域，他的工作不仅推动了理论发展，还在物理学、计算机科学、金融学、气象学等应用学科中产生了深远影响。他的思想至今仍是数学研究的重要源泉，被誉为“20世纪最伟大的数学家之一”。

SRE

站点可靠性工程（Site Reliability Engineering，SRE）是由Google提出的一种将软件工程方法应用于运维问题的实践框架，旨在通过自动化、数据驱动和工程化手段提升系统的可靠性与效率。其核心思想是将传统运维任务转化为可编程、可扩展的软件问题，从而实现对大规模分布式系统的高效管理。

以下是SRE的核心概念和岗位职责：

SRE的定义与原则

1. 工程化运维：SRE强调通过编写代码而非手动操作解决运维问题，例如自动化部署、监控和故障恢复。例如，Google的SRE团队通过自动化工具将重复性任务（如服务扩容）的耗时从小时级降至分钟级。

2. 服务等级目标（SLO）驱动：SRE通过定义明确的SLO（如99.9%可用性）和错误预算（Error Budget）来平衡新功能开发与系统稳定性。当错误预算耗尽时，团队需优先修复可靠性问题而非发布新功能。

3. 减少琐碎工作（Toil Elimination）：SRE要求将工程师的重复性操作（如手动扩缩容）控制在50%以下，剩余时间投入长期项目（如架构优化）。例如，Google通过自动化将告警处理时间缩短了90%。

4. 拥抱风险与快速迭代：SRE鼓励通过小规模、高频次的变更降低故障影响，结合灰度发布（Canary）和自动化回滚机制。

SRE的岗位职责

1. 系统可靠性保障：设计并维护监控告警系统，确保及时响应故障。 制定灾难恢复计划，定期进行故障演练（如“Wheel of Misfortune”模拟故障场景）。

2. 自动化与工具开发：开发工具替代人工操作，例如自动化部署流水线或自愈脚本。 案例：Google SRE团队通过自动化将数据库故障恢复时间从数小时缩短至分钟级。

3. 性能优化与容量规划：分析系统瓶颈，优化资源利用率（如通过负载均衡减少冗余资源）。 预测流量增长并提前扩容，避免服务过载。

4. 跨团队协作：与开发团队共同设计高可用架构，推动“生产就绪”标准（如混沌工程测试）。 通过标准化工具链（如统一监控平台）降低协作成本。

5. 文化倡导：推行无责（Blameless）文化，通过事后复盘（Postmortem）系统性改进。 培训开发团队掌握基础运维技能，促进所有权共享（Shared Ownership）。

SRE通过工程化手段将运维转化为可扩展、可持续的实践，同时平衡创新与稳定性，是现代云原生系统可靠运行的关键角色。，它与传统运维的区别包括：

• 主动性：SRE通过预防性工程（如自动化测试）减少故障，而非被动响应。

• 技术深度：SRE需具备软件开发能力，例如用Go/Python编写运维工具。

• 目标对齐：SRE与产品团队共享错误预算，确保业务目标与技术决策一致。

AI SRE Agent

随着数字化转型的加速和云原生技术的普及，现代系统的复杂性和规模呈指数级增长，传统SRE（站点可靠性工程）模式正面临巨大挑战。人工运维团队需要同时处理海量监控数据、多维度故障根因分析以及跨云环境的动态编排，这种高度依赖人工经验的响应方式已难以满足业务对”始终在线”的苛刻要求。在此背景下，AI SRE Agent的引入成为必然——它通过机器学习实时解析TB级日志和指标数据，以概率推理定位潜在故障点；利用强化学习算法自动优化告警阈值和响应策略，将MTTR（平均修复时间）缩短90%以上；更通过数字孪生技术模拟千万级并发场景，提前预测容量瓶颈。这种智能体不仅继承了SRE”工程化运维”的核心思想，更以AI的持续进化能力重构了可靠性管理的范式，使系统具备从”人工治愈”到”自愈”的质变可能。

AI SRE Agent（人工智能站点可靠性工程代理）是一种基于人工智能技术的自动化运维工具，旨在通过AI能力提升云环境或软件基础设施的可靠性、运维效率及事件响应速度，以下是其核心特点与功能：

1. 核心定义与目标

AI SRE Agent结合大型语言模型（LLM）的推理能力和自动化工具，模拟人类站点可靠性工程师（SRE）的工作流程，实现从监控到故障修复的闭环管理。其主要目标包括：

• 自动化根因分析（RCA）：快速诊断生产环境问题的根本原因，将传统需数小时的RCA缩短至分钟级。

• 主动运维：通过持续学习资源状态和性能趋势，预测并预防潜在故障，而非被动响应。

• 减轻工程师负担：减少重复性任务（如日志分析、告警处理），让团队专注于创新性工作。

2. 关键技术能力

• 智能监控与告警处理：集成Azure Monitor、PagerDuty等工具，实时响应告警并自动触发调查流程，访问指标、日志和依赖关系以形成假设。

• 自动化修复操作：在用户授权下执行修复动作，如扩展资源、重启应用、回滚部署等。例如，Azure SRE Agent支持对Azure Kubernetes服务（AKS）的Pod重启和版本回滚。

• 安全与合规管理：持续审核资源是否符合安全实践（如TLS版本、托管身份启用），并自动修复漏洞。

• 开发者协作闭环：生成包含详细诊断信息的GitHub Issue，帮助开发者修复代码并防止问题复发。

3. 与传统SRE的差异

• 自主性与学习能力：AI代理通过知识图谱和多层级记忆管理积累系统上下文，逐步优化决策。例如，Cleric能通过历史事件推断Redis内存压力可能导致级联故障。

• 多工具协同：支持与Kubernetes、Datadog、Slack等平台集成，调用API执行跨系统操作。

• 实时性与规模：并行处理数千个信号，同时分析日志、指标和追踪数据，远超人工处理速度。

4. 典型应用场景

• 云服务管理：如微软Azure SRE Agent专为Azure资源设计，提供每日健康报告和自动化缓解措施。

• 混合环境优化：AgentSRE等方案支持跨多云和本地基础设施的统一监控与修复。

• 金融与高可用系统：在银行等高风险场景中，AI代理通过预测性维护减少宕机损失。

5. 挑战与限制

• 实时数据依赖：代理需持续获取最新系统状态，数据延迟可能导致误判。

• 信任建立：初期需人类审核关键操作（如资金交易），逐步扩大自治范围。

• 成本控制：大规模部署可能带来算力与存储开销，需平衡效率与资源消耗。

6. 未来方向

行业正从“辅助诊断”迈向“自主修复”，如Traversal等公司通过多代理协作将平均修复时间（MTTR）降低90%。同时，AI SRE框架逐渐扩展至安全、网络等领域，形成跨职能的智能运维生态。

SRE通过工程化重构了运维的底层逻辑，而AI SRE Agent进一步将其推向智能化与自动化。两者的结合不仅解决了规模与复杂度的瓶颈，更重新定义了可靠性管理的边界——从“稳定优先”到“预测自愈”，最终实现系统韧性的质变。AI SRE Agent代表了运维自动化向智能化演进的关键技术，通过AI驱动的决策与行动，显著提升系统可靠性并释放工程师生产力。