20 世纪最具影响力的数学家之一

斯蒂芬·斯梅尔（Stephen Smale，1930年7月15日－）是20世纪最具影响力的数学家之一，以其在拓扑学、动力系统、经济学和计算理论等领域的开创性工作而闻名。他出生于美国密歇根州弗林特市的一个工程师家庭，从小展现出对数学的兴趣，但高中时期的学业表现并不突出。1948年，他进入密歇根大学学习物理，随后转向数学，并于1957年在拉乌尔·博特（Raoul Bott）的指导下获得博士学位，研究方向为微分拓扑。

斯梅尔的数学生涯充满了突破性贡献。1961年，他证明了五维及更高维度的庞加莱猜想（Poincaré Conjecture），这一成果震惊了数学界，并为他赢得了1966年的菲尔兹奖。他的证明方法引入了一系列拓扑方法和“h-配边定理”（h-cobordism theorem），这些工具成为微分拓扑领域的核心。他在动力系统领域的研究也极具影响力，特别是他构造的“马蹄映射”（Smale horseshoe），为混沌理论奠定了基础，并广泛应用于非线性动力学、气象学和生物数学等领域。

但是斯梅尔的学术生涯并非一帆风顺，他于1948年进入密歇根大学学习之后，他是一名不错的学生，被选入由鲍勃·索尔（Bob Thrall）教授的荣誉微积分课程，并取得了优异的A成绩。然而，在大学二年级和三年级期间，他的成绩平平，大多是B和C，甚至在核物理这门课上得了F。斯梅尔于1952年获得了理学学士学位。尽管成绩不佳，但凭借一些运气，他仍被密歇根大学数学系录取为研究生。然而，在研究生阶段的前几年，他的表现依然不佳，平均成绩仅为C。当系主任希尔德布兰特（Hildebrandt）威胁要将他开除时，他才开始更加认真地对待学业。最终，斯梅尔于1957年在拉乌尔·博特（Raoul Bott）的指导下获得博士学位，并开始在芝加哥大学担任讲师，由此开启了他的学术生涯。

在里约的沙滩上寻找马蹄映射

斯蒂芬·斯梅尔在1960年春天前往巴西里约热内卢的访问，成为他数学生涯中一段极具传奇色彩的经历。当时他获得了美国国家科学基金会（NSF）的资助，选择前往里约热内卢的纯粹与应用数学研究所（IMPA）进行学术交流。这段时期不仅孕育了他最重要的数学突破，也留下了”在里约海滩上完成伟大证明”的佳话。在里约工作期间，斯梅尔保持着独特的研究习惯，他常常带着笔记本来到著名的科帕卡巴纳海滩，在沙滩上思考数学问题。这种非传统的工作方式后来引发了一些争议，但也成为他创造性思维的象征。正是在这样的环境中，他同时完成了两项里程碑式的成果：动力系统中马蹄映射的发现和高维庞加莱猜想的证明。

马蹄映射（Smale horseshoe）的发现是斯梅尔在里约期间最重要的贡献之一，这一发现彻底改变了人们对动力系统的理解。当时斯梅尔正在研究结构稳定性问题，受到同事Mauricio Peixoto的启发，他开始深入思考动力系统的长期行为。在里约海滩上的思考中，他构造出一个简单而深刻的几何模型——马蹄映射，这个模型展示了一个确定性系统如何产生看似随机的行为。马蹄映射的核心思想是通过拉伸、折叠的几何变换，展现出动力系统中对初始条件的敏感依赖性，这后来成为混沌理论的基石之一。这一发现不仅为混沌现象提供了严格的数学描述，也为后来的动力系统研究开辟了全新方向。

在拓扑学领域，斯梅尔在里约期间完成了对高维庞加莱猜想的突破性证明。庞加莱猜想是拓扑学中最著名的未解决问题之一，其核心是探讨如何通过局部性质判断一个空间是否等同于球面。斯梅尔采用创新的微分拓扑方法，成功证明了该猜想在五维及更高维度上的正确性。他的证明引入了革命性的”斯梅尔手术”技术，通过系统地处理流形上的奇异点，最终建立了h-配边定理。这个定理不仅解决了庞加莱猜想的高维情形，还为流形的分类提供了强有力的工具。值得一提的是，斯梅尔在里约的证明过程极具个人特色，他常常在研究所和海滩之间往返，将深奥的拓扑思考与里约的自然环境奇妙地融合在一起。

而斯梅尔的数学觉醒始于他对庞加莱（Henri Poincaré）”同宿点”（homoclinic point）理论的重新发现。在里约热内卢数学研究所（IMPA）的图书馆里，斯梅尔偶然翻阅了美国数学家伯克霍夫（George Birkhoff）的著作集，其中详细记录了庞加莱在研究三体问题时提出的同宿点概念。庞加莱曾发现，在保守系统中，稳定流形和不稳定流形的横截相交会产生极其复杂的动力学行为，他将这种现象称为”同宿纠缠”。这一发现曾让庞加莱本人都感到震惊，以至于他在《天体力学新方法》中写道：”这一现象的复杂性令我震撼，我甚至不愿尝试描绘它的图景。”然而，这一深刻见解在随后的几十年里几乎被数学界遗忘，直到斯梅尔通过伯克霍夫的著作重新发现了它。

与此同时，斯梅尔正与动力系统领域的另一位关键人物——麻省理工学院的诺曼·莱文森（Norman Levinson）保持着密切的学术交流。莱文森在1949年对英国数学家卡特赖特（Cartwright）和利特尔伍德（Littlewood）关于非线性振动的研究进行了严格化，他们的工作揭示了某些微分方程中存在的复杂解行为。莱文森在给斯梅尔的信中指出了他早期猜想中的一个错误，这个批评成为斯梅尔思想转变的催化剂。斯梅尔后来回忆道：”莱文森的信像一道闪电，击碎了我原有的认知框架，迫使我重新思考动力系统的本质。”在里约海滩的反复推演中，斯梅尔将莱文森描述的复杂行为与庞加莱的同宿点理论联系起来，逐渐形成了”马蹄映射”的雏形。

前苏联数学家庞特里亚金（Lev Pontryagin）和安德罗诺夫（Alexander Andronov）的结构稳定性理论构成了影响斯梅尔的第三个重要思想来源。通过他在普林斯顿高等研究院的同事所罗门·莱夫谢茨（Solomon Lefschetz），斯梅尔接触到了苏联学派关于”粗糙系统”（即结构稳定系统）的研究。庞特里亚金和安德罗诺夫在1937年提出，许多物理系统可以用在微小扰动下保持定性性质的动力系统来描述。斯梅尔的巴西同事莫里斯·佩肖托（Mauricio Peixoto）曾跟随莱夫谢茨学习，他将这一理论传统带到了巴西。斯梅尔敏锐地意识到，庞特里亚金的结构稳定性理论与他自己正在思考的问题存在深刻联系，但苏联学派的研究因排除了同宿现象而显得过于局限。

在这三重理论背景的交织下，斯梅尔于1960年初在里约的海滩上完成了他的两大突破。在科帕卡巴纳海滩的某个下午，他忽然领悟到庞加莱的同宿点必然导致马蹄结构的出现。他后来描述这一顿悟时刻：”当我将同宿点的概念与莱文森描述的复杂行为联系起来时，整个图景突然变得清晰起来。”马蹄映射的精妙之处在于，它通过简单的几何操作（拉伸、折叠）展现了确定性系统中的内在随机性：一个二维映射将正方形区域拉伸变窄后折叠成马蹄形，通过迭代这个过程，系统会表现出对初始条件的极端敏感性——这正是混沌的核心特征。斯梅尔证明，这种马蹄结构在出现同宿点的系统中是普遍存在的，从而为混沌现象提供了第一个严格的数学框架。

几乎在同一时期，斯梅尔在拓扑学领域也取得了惊人突破。多年来，他一直被庞加莱猜想所困扰，这个猜想探讨如何通过代数不变量来识别球面。在里约期间，斯梅尔发展出了一套全新的微分拓扑方法。他创造性地将动力系统中的思想引入拓扑学，提出了”斯梅尔手术”技术，通过系统地处理高维流形上的奇异点，最终证明了五维及更高维度的庞加莱猜想。这一证明的关键在于h-配边定理的建立，该定理表明在某些条件下，两个流形之间的配边实际上是一个平凡配边。斯梅尔后来回忆，这一突破同样发生在里约的海滩上：”有一天，当我看着海浪周而复始地拍打沙滩时，突然想到了如何通过逐层消解流形上的奇点来构造同胚。”

斯梅尔在里约的这段科研经历展现了跨学科思想交融的强大创造力。他将庞加莱的天体力学直觉、莱文森的严格分析技巧和庞特里亚金的结构稳定性观点融为一体，最终在动力系统和拓扑学两个领域同时取得重大突破。这种独特的学术轨迹也反映了20世纪中叶数学发展的一个显著特征：不同学派、不同传统的数学思想在全球范围内的流动与碰撞。斯梅尔的工作不仅解决了具体难题，更重要的是建立了连接不同数学分支的新范式，为后续的混沌理论、微分拓扑和动力系统研究开辟了广阔的道路。正如他后来所说：”数学中最美妙的事情往往发生在你让不同领域的想法自由对话的时候。“斯梅尔后来回忆说，里约的海滩为他提供了理想的思考环境，阳光、海浪和轻松的氛围帮助他突破了传统思维的束缚。这种非传统的工作方式虽然一度引起NSF对其研究经费使用的质疑，但最终产出的卓越成果证明了其有效性。斯梅尔的这段经历也成为数学史上的一个传奇，展示了伟大数学发现可能诞生在最意想不到的环境之中。从马蹄映射的发现到庞加莱猜想的证明，斯梅尔在里约的短暂停留永久地改变了多个数学领域的发展轨迹。

斯梅尔马蹄映射

斯梅尔马蹄映射（Smale’s Horseshoe Map）是动力系统理论中的一个经典模型，由数学家Stephen Smale在1960年代提出。它通过简单的几何变换，揭示了混沌动力系统中的复杂行为，如无限周期轨道、非周期轨道以及拓扑熵的存在。马蹄映射的核心在于拉伸、折叠和压缩的操作，使得系统在迭代过程中产生高度复杂的动力学行为。

1. 马蹄映射的几何构造

初始设定

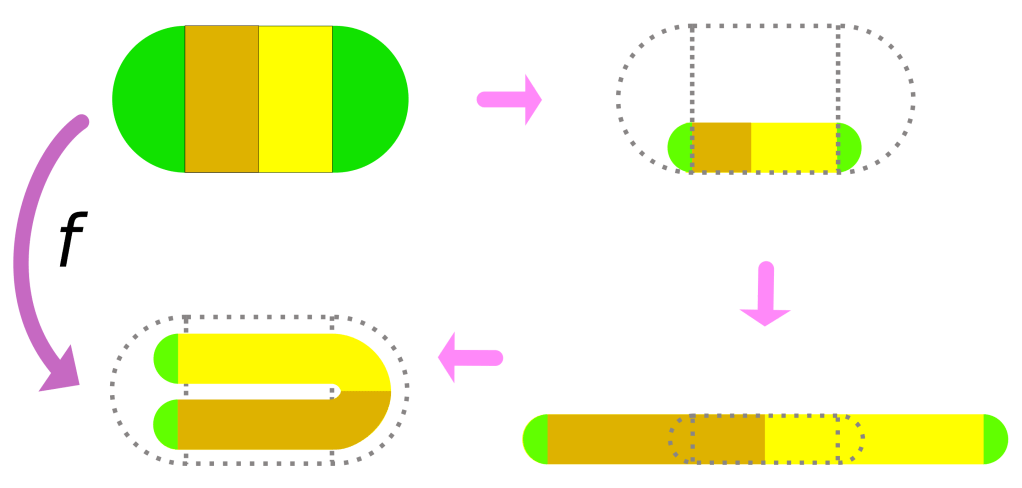
考虑一个矩形区域 （例如单位正方形 ）。马蹄映射 的作用是将这个矩形进行非线性拉伸和折叠，使其在水平方向上拉长，在垂直方向上压缩，并弯曲成“马蹄”形状。

拉伸与折叠

1. 水平拉伸：首先，矩形 DDD 在水平方向上被拉伸（例如，长度变为原来的 倍，）。

2. 垂直压缩：同时，在垂直方向上，矩形被压缩（高度变为原来的 倍，）。

3. 弯曲折叠：拉伸后的长条被弯曲成“U”形或“马蹄”形，并重新放置在原矩形区域上方，使得它横跨原矩形的两个垂直条带（例如，左右各占一部分）。

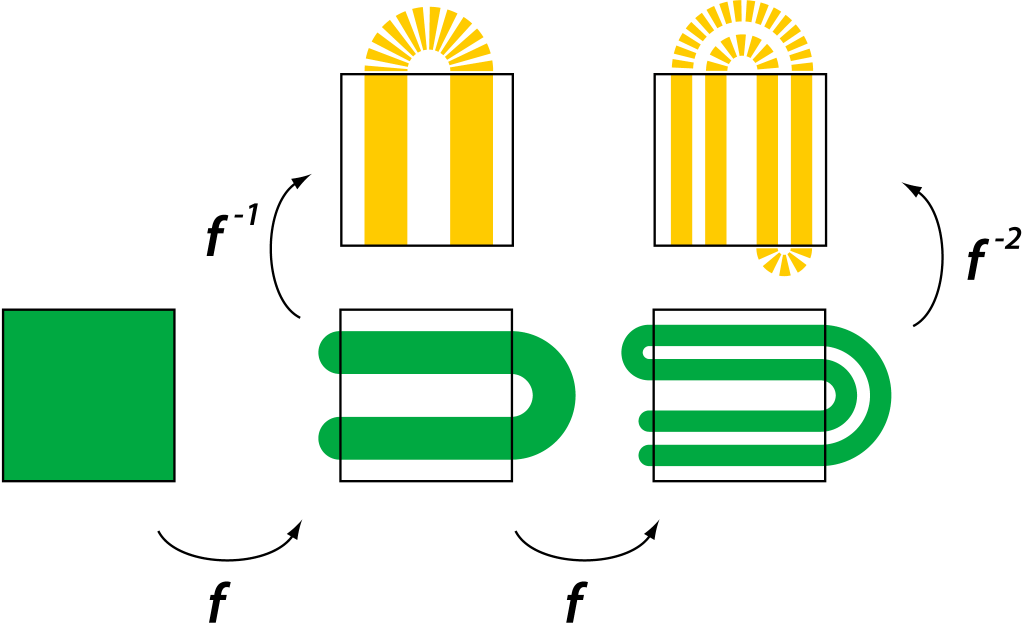
迭代过程

每次应用映射 ，矩形都会被拉伸、压缩并折叠一次。逆映射 则相当于反向操作，即垂直拉伸、水平压缩，并反向折叠。

2. 马蹄映射的动力学行为

不变集与混沌

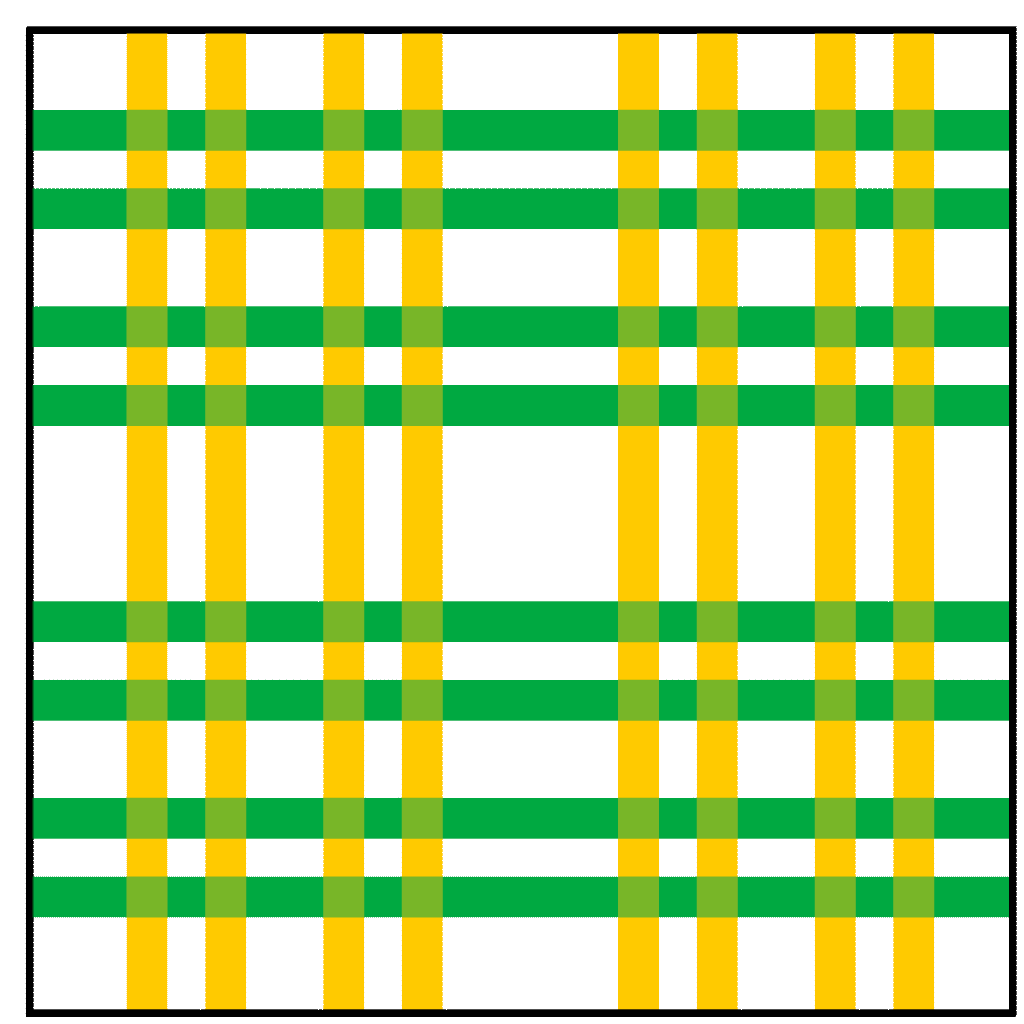
在无限次迭代后，某些点永远不会离开矩形 ，这些点的集合称为不变集 。 是一个Cantor集（分形结构），由无限多个离散点组成，具有自相似性。这个不变集上的动力学行为是混沌的，即：存在无限多个周期轨道（任意长度的周期），存在非周期轨道（永不重复的轨道），系统对初始条件敏感依赖（微小变化导致长期行为完全不同）。

符号动力学与混沌

马蹄映射的不变集 可以与符号动力学（Symbolic Dynamics）对应：每个轨道可以用一个二进制序列（如 ）表示，其中“0”和“1”分别代表点在每次迭代中落在左侧或右侧条带。这种对应关系表明，马蹄映射的动力学行为等价于伯努利移位（Bernoulli Shift），即一个无限符号序列的混沌系统。

3. 马蹄映射的意义

Smale 马蹄映射是第一个严格证明的混沌系统之一，它展示了如何从简单的几何变换中产生极其复杂的动力学行为。它解释了横截同宿点（Transverse Homoclinic Points）的存在如何导致混沌（Poincaré曾发现同宿点，但Smale用马蹄映射严格证明了混沌的存在）。它广泛应用于非线性动力系统领域、天体力学、工程与物理中。

4. 直观理解

想象一个橡皮筋被拉伸、压缩并折叠成一个马蹄形，然后再次拉伸、压缩并折叠。每次操作都会使橡皮筋的结构更加复杂，最终形成一个无限精细的网状结构（Cantor集）。在这个结构中，任何微小的扰动都会导致完全不同的未来轨迹，这正是混沌的本质。Smale马蹄映射的美妙之处在于，它用如此简单的几何操作，揭示了自然界中广泛存在的混沌现象。它不仅是一个数学构造，更是理解复杂动力系统的一把钥匙。

斯梅尔的学术生涯

在学术职位上，斯梅尔曾先后任教于哥伦比亚大学（1960–1964）、加州大学伯克利分校（1964–1995）和香港城市大学（1995–2002），并在伯克利分校退休后成为荣誉教授。在2003至2012年期间，斯梅尔担任丰田工业大学芝加哥分校的教授；此外自2009年8月1日起，他开始担任香港城市大学的特聘教授。斯梅尔的研究兴趣广泛，晚年还涉足计算理论和数理经济学。他研究了“牛顿法”在数值计算中的收敛性问题，并提出了“斯梅尔问题”（Smale’s problems），即“P vs. NP”问题的数值版本。在经济学领域，他与经济学家合作，探讨了一般均衡理论和市场动态的数学结构。他的多学科研究展现了他对数学及其应用的深刻理解。

斯梅尔的卓越贡献为他赢得了多项顶级荣誉，包括菲尔兹奖（1966）、美国国家科学奖章（1996）和沃尔夫数学奖（2007）。他的工作不仅解决了高维庞加莱猜想这样的重大难题，还推动了动力系统、计算理论和经济学的发展。许多数学概念以他的名字命名，如斯梅尔马蹄、斯梅尔手术和斯梅尔问题，这些成果至今仍在数学和科学领域产生深远影响。

2002年退休后，斯梅尔仍保持对数学研究的热情。他的职业生涯体现了数学家对社会责任的关注，以及跨学科研究的价值。正如数学家迈克尔·阿蒂亚（Michael Atiyah）所说：“斯梅尔是那种罕见的数学家，他不仅能解决难题，还能改变整个数学的走向。”斯蒂芬·斯梅尔的生平和成就，无疑为现代数学留下了不可磨灭的印记。