刚入学新加坡国立大学（NUS）时，作为一名数学博士，我为自己设定了一个明确的目标：在四大数学期刊上发表论文，即《Annals of Mathematics》、《Inventiones Mathematicae》、《Journal of the American Mathematical Society》和《Acta Mathematica》。这个目标是我科研生涯早期最重要的方向，也是我不断努力的动力源泉。

然而，博士第二年下学期，我的科研进入了困境。思路受阻，进展缓慢，那段时间我常常感到迷茫和焦虑，陷入了低效的恶性循环。进入博士第三年上学期，我重新振作，奋发图强，努力推进研究工作，取得了一些进展。但到了下学期，我再次陷入了科研瓶颈。那段时间，我深刻感受到拖延和自我怀疑所带来的负面影响。

幸运的是，在博士第三年下学期临近结束时，我读到了《战胜拖拉》这本书。这本书对我的影响深远，它帮助我认识到自己在时间管理和心理抗阻上的问题，也让我明白了持续努力的重要性。在调整了心态与习惯后，我的研究终于取得独立突破，完成了Real Bound Theorem的结果。这一阶段的成功，我由衷地感谢《战胜拖拉》。博士第四年，我保持了相对稳定且高效的节奏。几乎每周七天都在工作，平均每天有三小时左右的高质量研究时间。虽然听起来不多，但这三小时的专注深度和效率，为我带来了持续的产出与成长。

大约是在2014年的时候，也就是我博士第四年的时候，可能记忆有偏差。有一次师门几人在Dover聚餐，其中包括导师、大师兄、三师兄还有我。导师问我们几人：“你们几个最近每天花在科研上的时间有多少，是一个小时还是两个小时？”大家顿时沉默不言。当时我阅读了《战胜拖拉》且颇有心得，我确实也按照书中所说治疗本人的拖延症，每天至少也有三个小时投入写论文中。我就如实告知导师。导师立刻说：“三个小时是肯定不够的，你最后的结果不会太差”。回头看上去，最后的结果也不算太差，能够正常搞完论文，当然出路也不算太好，要凭借自己的实力留在学术圈要也比较困难。

我毕业之后，师门几个人也逐渐从国外回国了。后来到了2021~2022年的时候，看到另外一位师弟在四大（Inventiones Mathematicae）上发表了一篇文章，所在学校专门报道了这件事情，我认真阅读了一下里面的内容，其中有几句话印象颇深。

导师一般会布置三个层次的课题，分别是：第一个课题锻炼学生独立思考的能力，第二个课题培养学生独立解决问题的能力，第三个课题让学生独立找到一个有意思的问题并独立解决。

看到这里，回想起来自己大概只完成了第一个课题，也就是Wild Cantor Attractors在Fibonacci-like区间映射上的存在性。要是严格说起来，也没有锻炼出太多独立思考的能力，但是绝对培养了我坚韧不拔的能力和抗压能力，让我以后面对工作难题的时候总能够迎难而上。

为什么我只能完成第一个课题？这可能与博士前三年投入的时间和精力有关。博士第一年大部分时间都花在了应对各种研究生考试和博士生资格考试上。在这一年内，我完成了七门数学课程的学习，并一次性通过了两门博士资格考试。第二年第一学期，我顺利通过了博士资格考试的口试部分和开题报告。问题出现在第二年第二学期，科研进展和状态陷入了恶性循环。论文进展缓慢，思路难以展开，每当看到论文就头大，整个人也不知道自己在做什么，反正浑浑噩噩地度过了这一年。直到第三年第一学期，我才努力奋起直追，开始有了些论文阅读的进展，但很快在第三年第二学期又陷入了恶性循环。直到第三年第二学期接近结束时，我才成功完成了Real Bound Theorem的研究成果。第四年的两个学期，我都在努力追赶进度，终于在第四年结束时，完成了论文的框架和细节整理。博士第五年第一学期，我将论文整理完毕并提交，第二学期顺利完成答辩。

问题的根源在于，博士第二年和第三年我陷入了迷茫，浪费了许多时间，导致我没有足够的时间投入到第二个课题和第三个课题上。然而，尽管如此，我还是从导师那里得到了第二个课题。在博士第四年，当我基本搞定第一个课题，并有把握将其写成毕业论文时，导师立刻给了我第二个课题。这个课题的描述是这样的：

Conjecture. 是否可以找到一个光滑的区间映射，使得通过迭代构造的类Cantor集合具有正的勒贝格测度？

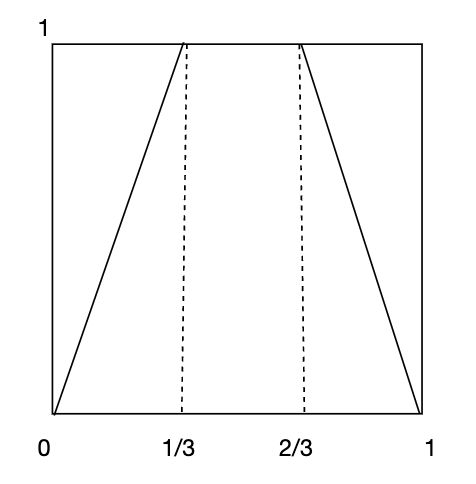
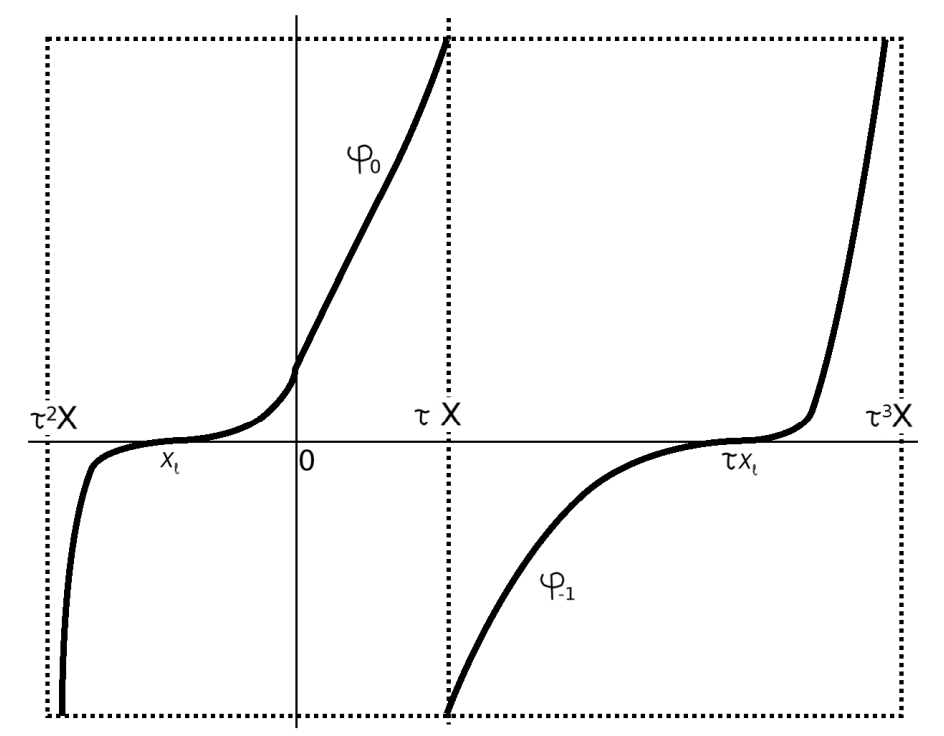
大家都知道，假设我们选择一个合适的函数 f，其形式类似于构造Cantor三分集合的过程。也就是说，Cantor三分集合可以表示为：\cap_{n=1}^{\infty}f^{-n}([0,1]) ，通过直接计算可以得出，Cantor三分集合的勒贝格测度为零。然而，问题在于是否能够找到一个新的区间映射f，通过迭代的方式构造出一个类Cantor集合，且该集合具有正的勒贝格测度？

当然，这个问题的难度非常大。当初我拿到这个问题时，导师对我说：“这个问题我不做了，你自己去做吧。”于是，我努力了一个多月，尽管没有找到明显的进展，但我发现这个区间映射的Real Bound Theorem与我之前做的有很大差异。毕业后，我没有继续研究这个问题。十年后，我再次搜索相关文献，依然没有找到明确的结论。与此同时，第二个课题也让我陷入了困境，以至于当时我已没有精力去独立寻找第三个课题了。

认真对比我与师弟的科研状态，其实有一些相似之处，也有明显的差异。相似的是，在前期我们都花了大量时间阅读难度极高的论文。师弟花了一年时间“啃”完一篇50页的四大顶刊论文，我当年也差不多，前期几乎花了半年到一年的时间才能真正读懂核心文献。但在工作状态和心态上，我们的差异就比较明显了。师弟在报告中提到，他坚持每天晚上11点睡觉、早上7点起床，中午午休半小时，保持全天的高效工作。而我当年明显做不到这一点，我平均每天在论文上的高质量工作时间大约只有3小时，其余时间基本没有投入到科研中。在心态方面，师弟似乎很早就认识到，做基础研究必须接受失败是常态，要学会保持积极的心态。而我直到博士第三年结束时，才真正意识到这一点的重要性。师弟还会每天自问：“今天有没有什么想学的知识、想看的文章？”他相信长期积累终会带来突破。而我当时基本上不会主动提出问题或设定目标，通常是导师给我什么论文，我就读什么论文，同时在毕业之前导师给的任务我一定都会完成。

应该是在2024年初，我和大师兄、二师兄一起吃饭时，大师兄突然提到一句话：“你只是在一个不太合适的时候，‘不想搞数学’的心态战胜了自己‘搞数学’的心态，导致你离开了数学。而这个时期，恰好是毕业的时刻，是你人生的一个拐点。”

那一刻，我不禁陷入了沉思。确实，那个时刻我并没有完全做好准备去继续面对数学研究的挑战，也许是因为心态的不稳定，才让自己在毕业的时候做出了放弃的决定。这句话让我意识到，心态在决定人生轨迹中的重要性，有时候一个小小的心态转变，就可能改变未来的方向。就像动力系统一样，初始值的一个微小变化都有可能导致未来轨迹的巨大变化。或许，这也是一个反思的契机，提醒我无论面对怎样的挑战，都不应该轻易被自己的情绪和心态所左右，而是要保持坚定和清晰的目标。人生的每一个转折点，都是自我成长的一部分，重要的是从中吸取教训，继续前行。