引言

在数学的世界中，有一种特殊的几何形态——分形。分形不仅仅是由简单规则生成的复杂图形，还由于它们呈现出自相似性（self-similarity），在更细微的尺度上微观显示出相似甚至相同的结构。除了 Cantor 三分集之外，Koch 曲线和 Koch 雪花同样是数学界最著名的分形图形之一。

Koch 曲线，最早由瑞士数学家海里格·冯·科赫 （Niels Fabian Helge von Koch）在 1904 年提出，其撰写论文是《Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire》，翻译成中文就是《关于一条连续而无切线，可由初等几何构作的曲线》。确实 Koch 曲线是一种由递归定义的分形曲线，就和 Cantor 三分集一样，通过简单的几何操作，即可创造出美妙的图形。在构造的过程中，Koch 曲线展现出了如何在有限的范围内呈现出长度是无穷的曲线。

而当我们在 Koch 曲线的基础上进行进一步的扩展，在一个三角形的基础上用一样的方式来构造，便得到了著名的 Koch 雪花。Koch 雪花是一种由多个相同的自相似三角形组成的分形图案，因其形状类似雪花而得名。它的构造过程是基于 Koch 曲线的迭代扩展，但在每个迭代步骤中加入了更多的三角形，使得雪花的外形更加复杂与精细。

在本文中，我们将深入探讨 Koch 曲线和 Koch 雪花的构造原理和数学特征。

Koch 曲线的构造过程

Koch 曲线的经典构造方法

现在，让我们来看一下 Koch 曲线的构造步骤究竟是什么样的？值得注意的是，这一过程在某种程度上与Cantor三分集的构造方式有着异曲同工之妙。Koch 曲线构造的详细步骤如下：

1. 从一条线段开始：假设初始线段的长度是 ；
2. 将这条线段三等分：于是每段的长度都是 ；
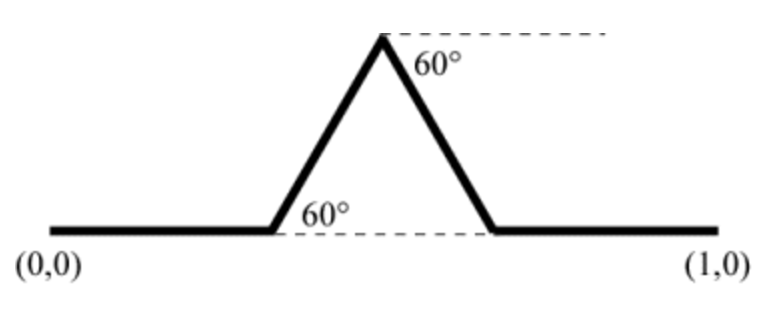
3. 构造三角形：在中间的线段上，构造一个等边三角形，其底边与中间的线段重合。也就是说，这个等边三角形的边长是 ；
4. 移除线段：移除原有线段中间的部分，即去掉与三角形底边相重合的那一段
5. 重复步骤 2 至 4：将每个新的小线段重复以上步骤。对每个新的小线段，按相同的方法进行分段、添加三角形并移除原中间部分。每次迭代后，曲线将变得更加复杂。
6. 无穷迭代：理论上，我们可以无限次地重复这个过程。而最终得到的曲线就是 Koch 曲线。

在构建等边三角形的时候，我们可以得到其角度是 ，如图所示。

然后随着迭代次数的增加，Koch 曲线上的“小三角形”将会变得越来越多。

L 系统

除此之外，Koch 曲线还可以使用 L-system 来进行构造；所谓的 L 系统（L-system）指的是 Lindenmayer 系统，它是由荷兰乌特勒支大学的生物学和植物学家，匈牙利裔的阿里斯蒂德·林登麦伊尔（Aristid Lindenmayer）于 1968 年提出的有关生长发展中的细胞交互作用的数学模型，尤其被广泛应用于植物生长过程的研究。 L-system 是一系列不同形式的正规语法规则，多被用于植物生长过程建模，但是也被用于模拟各种生物体的形态。L-system 也能用于生成自相似的分形，例如迭代函数系统。

而 Koch 曲线中的 L 系统指的是满足以下规则的构造方式，即可构造出 Koch 曲线。它的规则是：F -> F−F++F−F，其中， 表示向前， 表示左转 ， 表示右转 。通过这样的方式，我们可以得到与经典构造方法一样的 Koch 曲线。

Koch 曲线的长度

从 Koch 曲线的构造过程不难看出，假设初始状态下线段的原始长度是 ，那么迭代了一次之后，长度变成了 。也就是说，每一次的迭代，都会使得总的长度变成原来的 倍。由于

，

所以 Koch 曲线的长度是无穷大。

Koch 曲线的 Hausdorff 维度

在传统的欧几里得几何中，维度通常是一个直观且确定的整数，例如线段是一维，平面是二维，立体是三维。然而，在分形几何中，许多复杂的图形无法用整数维度来精确描述。这时，引入一种更广义的维度概念Hausdorff 维度，使得我们能够量化这些图形的复杂性。Hausdorff 维度通过研究几何物体的自相似性和递归结构，将维度扩展为一个可能是分数的数值。它描述了一个物体在放大或缩小过程中点分布的稠密程度，尤其适用于分形图形。

首先，我们给出 Hausdorff 维度的定义。考察一个特殊的几何物体，这个物体由 个大小一致且互不重叠的小物体组成，这些小物体的形状和这个物体本身相同。若这些小物体和大物体的大小比例为 ，也就是说小物体放大 倍之后与大物体完全重合，那么这个几何物体的 Hausdorff 维度（豪斯多夫维数）就定义为

，

换言之，。

其次，我们说明这样的维度定义与传统意义上的整数维度是不矛盾的。

• 线段（一维）：一条长度为 的线段可以被分成 段（），每段的长度与原来线段的大小比例是 （），因此 Hausdorff 维度是 。
• 正方形（二维）：一个边长为 的正方形可以被分成 个边长是 的小正方形，每一个小正方形与原来正方形的大小比例是 （），因此 Hausdorff 维度是 。
• 正方体（三维）：一个边长为 的正方体可以被分成 个边长是 的小正方体，每一个小正方体与原来正方体的大小比例是 （），因此 Hausdorff 维度是 。

再次，我们来看一下 Koch 曲线的 Hausdorff 维度。从 Koch 曲线的构造过程不难看出，Koch 曲线是由 4 条小曲线构成的，而这 4 条小曲线是互相全等的，并且小曲线放大 3 倍就与原来的 Koch 曲线重合。所以，Koch 曲线的 Hausdorff 维度就是

。

于是，我们已经看到了一条 Hausdorff 维度并不是整数的曲线，它的 Hausdorff 维度介于 与 之间。

Koch 雪花的构造过程

Koch 雪花的经典构造方法

当我们将 Koch 曲线的构造从单条线段扩展到整个几何图形的时候，一个令人惊叹的分形图案便随之诞生——这就是 Koch 雪花。它从一个简单的等边三角形出发，通过对每条边不断应用 Koch 曲线的迭代规则，逐步生成出精美复杂的图案。相比于单条 Koch 曲线，Koch 雪花展现了更为对称和完整的分形之美。接下来，让我们一起来了解 Koch 雪花的构造过程。

从一个等边三角形开始，我们可以对等边三角形的每一条边都进行 Koch 曲线的变形，然后一直无穷地迭代下去，就可以得到一个 Koch 雪花。

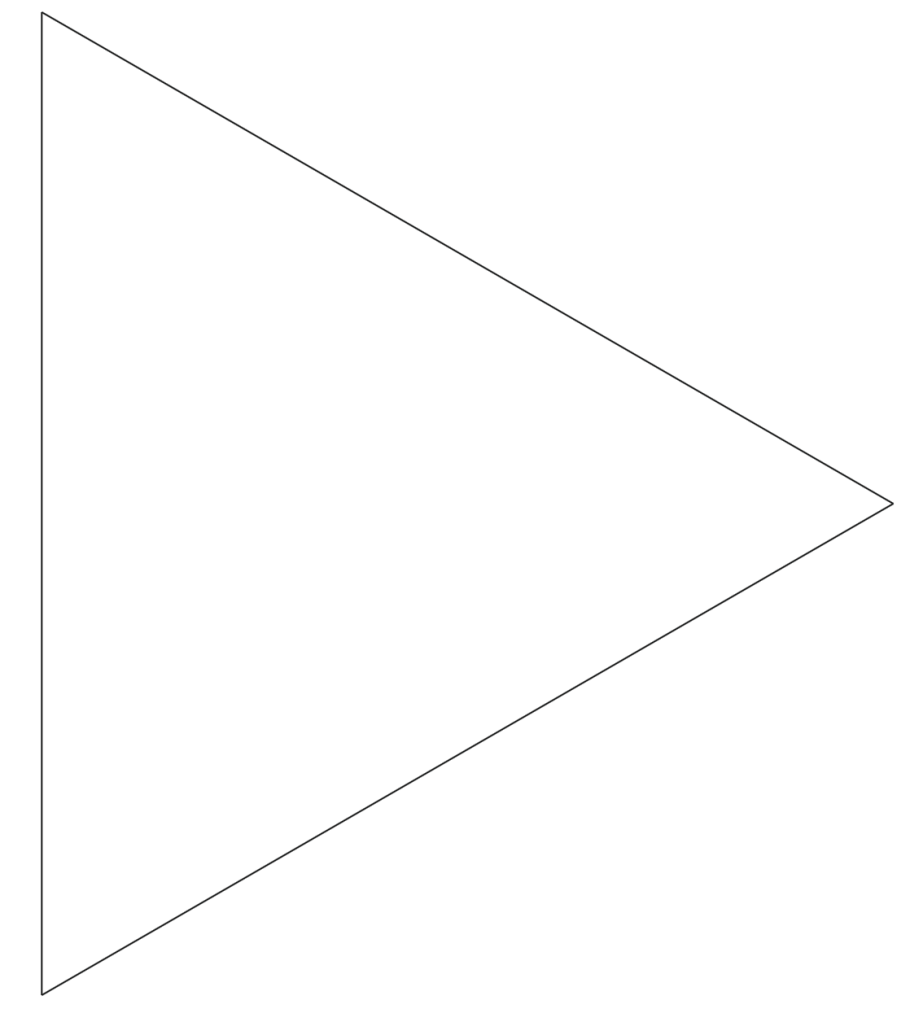
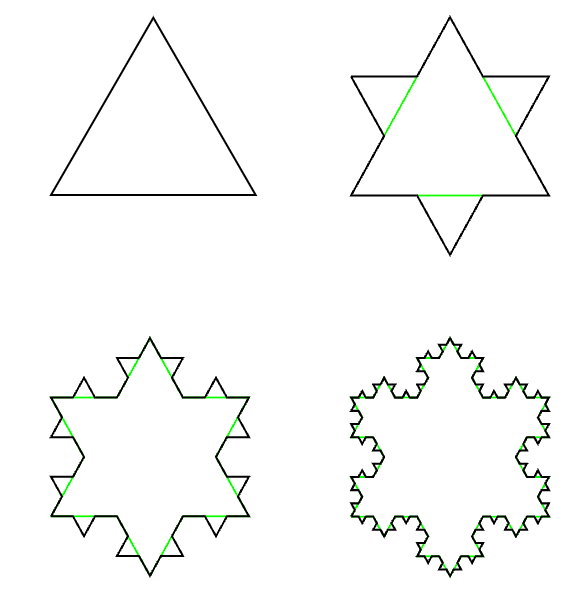
第一步：先画一个等边三角形，这里对应的是迭代次数 。

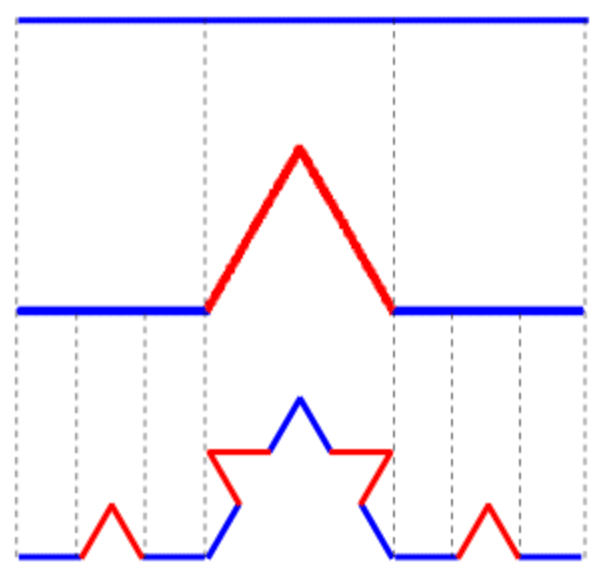
第二步：等边三角形的每一条边都用 Koch 曲线的演变规则，于是变成下图所示，这里对应的是迭代次数 。

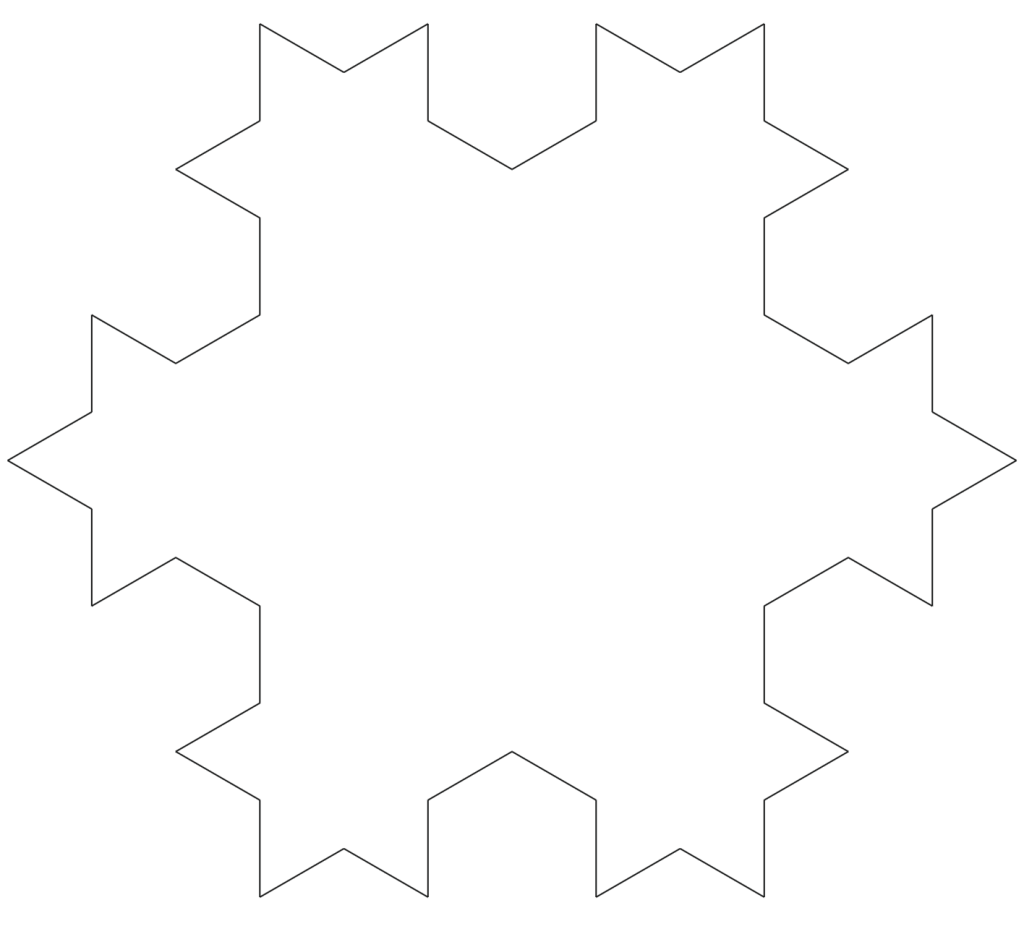
第三步：上述图形的每一条边都进行一模一样的 Koch 曲线演变，我们逐步获得以下的三幅图，分别对应着迭代次数 。

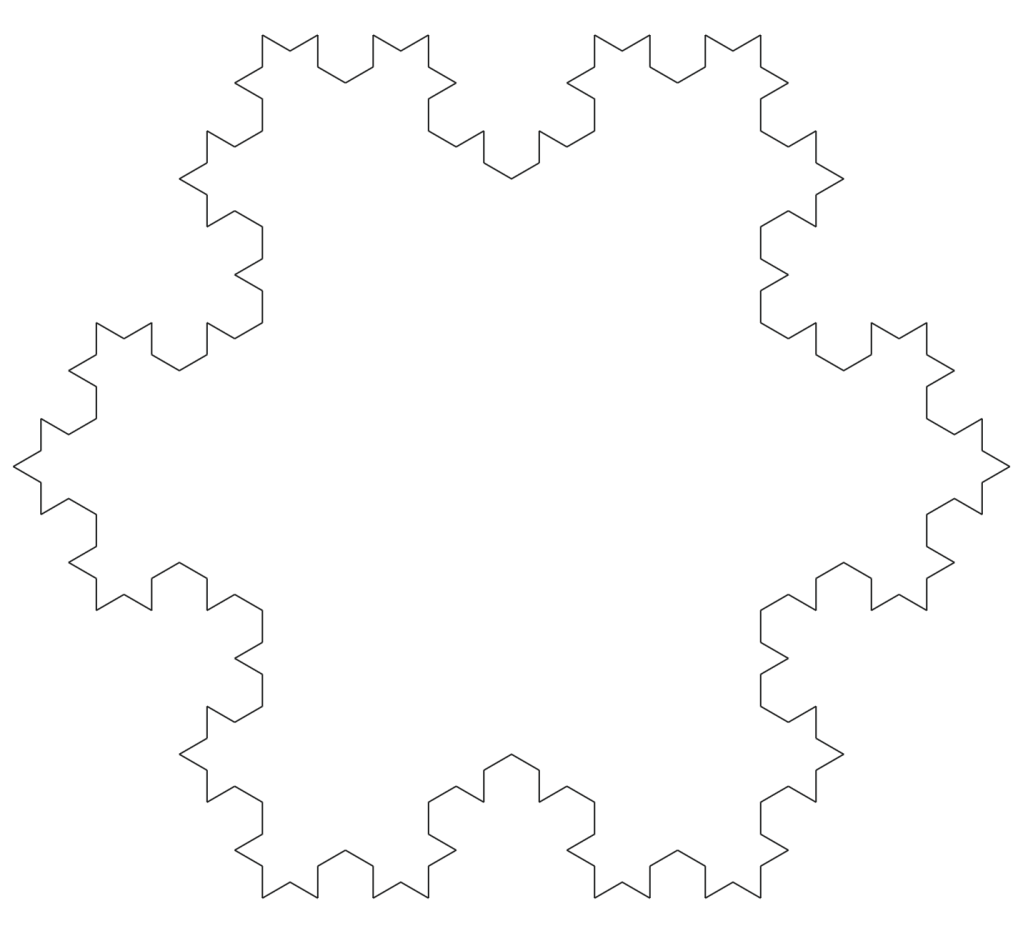
至此为止，我们已经可以看到一个基于正三角形而形成了雪花状的图形，当迭代次数趋向于无穷的时候，我们就得到了最终的 Koch 雪花（Koch Snowflake）。

Koch 雪花的周长与面积

Koch 雪花作为一种经典的分形图形，展示了一个令人惊奇的现象：通过之前的分析我们已经知道 Koch 曲线的长度是无穷大，那么由 Koch 曲线构造出来的 Koch 雪花，它的周长自然就是无穷大。尽管其周长是无穷大的，但其面积却是有限的。通过逐步迭代 Koch 曲线，我们构建出了这个美丽的雪花图案。在每一步迭代中，虽然新的小三角形不断增加，使得周长变得越来越大，但由于每个小三角形的面积逐渐变小，它们对整体面积的贡献变得微不足道。接下来，我们将详细计算 Koch 雪花的面积，揭示这种看似矛盾的现象背后的数学原理。

假设 是初始三角形的面积， 表示第 $n$ 次迭代的三角形面积，其中 。

第一次迭代：初始三角形的边有 条，在第一次迭代的时候会生成三个小三角形，每一个小三角形的面积是初始的 ，同时从 条边变成了 条边。也就是说：

。

第二次迭代：边有 条，可以生成 个更小的三角形，每一个更小的三角形的面积是初始三角形面积的 ，同时从 条边变成了 条边。也就是说：

。

以此类推，我们可以得到递推公式如下，当 时，

成立。将递推公式求和之后我们可以得到

当 趋向于无穷的时候，。

因此，Koch 雪花是一个周长无穷大，但是面积却是有限的图形。

结束语

通过对 Koch 曲线、Koch 雪花的深入探讨，我们不仅领略了它们的美丽与复杂，还理解了如何通过数学语言描述自然界中的自相似结构。从 Koch 曲线的无限延伸到 Koch 雪花的有限面积，从 Hausdorff 维度对不规则形状的精准量化到 L 系统在分形生成中的应用，这些概念和工具为我们提供了新的视角去探索复杂的几何现象和数学性质。