SRE

站点可靠性工程（Site Reliability Engineering，SRE）是由Google提出的一种将软件工程方法应用于运维问题的实践框架，旨在通过自动化、数据驱动和工程化手段提升系统的可靠性与效率。其核心思想是将传统运维任务转化为可编程、可扩展的软件问题，从而实现对大规模分布式系统的高效管理。

以下是SRE的核心概念和岗位职责：

SRE的定义与原则

1. 工程化运维：SRE强调通过编写代码而非手动操作解决运维问题，例如自动化部署、监控和故障恢复。例如，Google的SRE团队通过自动化工具将重复性任务（如服务扩容）的耗时从小时级降至分钟级。

2. 服务等级目标（SLO）驱动：SRE通过定义明确的SLO（如99.9%可用性）和错误预算（Error Budget）来平衡新功能开发与系统稳定性。当错误预算耗尽时，团队需优先修复可靠性问题而非发布新功能。

3. 减少琐碎工作（Toil Elimination）：SRE要求将工程师的重复性操作（如手动扩缩容）控制在50%以下，剩余时间投入长期项目（如架构优化）。例如，Google通过自动化将告警处理时间缩短了90%。

4. 拥抱风险与快速迭代：SRE鼓励通过小规模、高频次的变更降低故障影响，结合灰度发布（Canary）和自动化回滚机制。

SRE的岗位职责

1. 系统可靠性保障：设计并维护监控告警系统，确保及时响应故障。 制定灾难恢复计划，定期进行故障演练（如“Wheel of Misfortune”模拟故障场景）。

2. 自动化与工具开发：开发工具替代人工操作，例如自动化部署流水线或自愈脚本。 案例：Google SRE团队通过自动化将数据库故障恢复时间从数小时缩短至分钟级。

3. 性能优化与容量规划：分析系统瓶颈，优化资源利用率（如通过负载均衡减少冗余资源）。 预测流量增长并提前扩容，避免服务过载。

4. 跨团队协作：与开发团队共同设计高可用架构，推动“生产就绪”标准（如混沌工程测试）。 通过标准化工具链（如统一监控平台）降低协作成本。

5. 文化倡导：推行无责（Blameless）文化，通过事后复盘（Postmortem）系统性改进。 培训开发团队掌握基础运维技能，促进所有权共享（Shared Ownership）。

SRE通过工程化手段将运维转化为可扩展、可持续的实践，同时平衡创新与稳定性，是现代云原生系统可靠运行的关键角色。，它与传统运维的区别包括：

• 主动性：SRE通过预防性工程（如自动化测试）减少故障，而非被动响应。

• 技术深度：SRE需具备软件开发能力，例如用Go/Python编写运维工具。

• 目标对齐：SRE与产品团队共享错误预算，确保业务目标与技术决策一致。

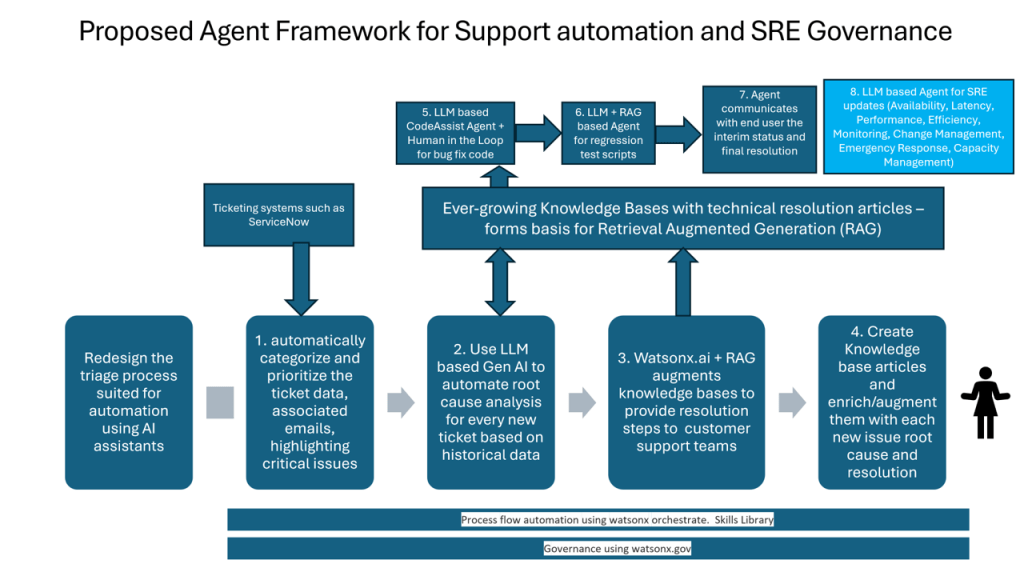
AI SRE Agent

随着数字化转型的加速和云原生技术的普及，现代系统的复杂性和规模呈指数级增长，传统SRE（站点可靠性工程）模式正面临巨大挑战。人工运维团队需要同时处理海量监控数据、多维度故障根因分析以及跨云环境的动态编排，这种高度依赖人工经验的响应方式已难以满足业务对”始终在线”的苛刻要求。在此背景下，AI SRE Agent的引入成为必然——它通过机器学习实时解析TB级日志和指标数据，以概率推理定位潜在故障点；利用强化学习算法自动优化告警阈值和响应策略，将MTTR（平均修复时间）缩短90%以上；更通过数字孪生技术模拟千万级并发场景，提前预测容量瓶颈。这种智能体不仅继承了SRE”工程化运维”的核心思想，更以AI的持续进化能力重构了可靠性管理的范式，使系统具备从”人工治愈”到”自愈”的质变可能。

AI SRE Agent（人工智能站点可靠性工程代理）是一种基于人工智能技术的自动化运维工具，旨在通过AI能力提升云环境或软件基础设施的可靠性、运维效率及事件响应速度，以下是其核心特点与功能：

1. 核心定义与目标

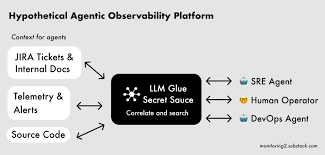
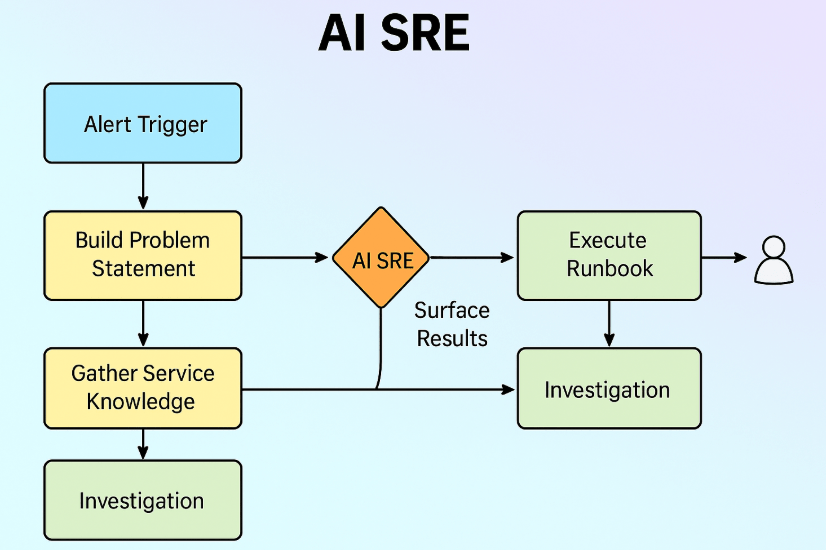
AI SRE Agent结合大型语言模型（LLM）的推理能力和自动化工具，模拟人类站点可靠性工程师（SRE）的工作流程，实现从监控到故障修复的闭环管理。其主要目标包括：

• 自动化根因分析（RCA）：快速诊断生产环境问题的根本原因，将传统需数小时的RCA缩短至分钟级。

• 主动运维：通过持续学习资源状态和性能趋势，预测并预防潜在故障，而非被动响应。

• 减轻工程师负担：减少重复性任务（如日志分析、告警处理），让团队专注于创新性工作。

2. 关键技术能力

• 智能监控与告警处理：集成Azure Monitor、PagerDuty等工具，实时响应告警并自动触发调查流程，访问指标、日志和依赖关系以形成假设。

• 自动化修复操作：在用户授权下执行修复动作，如扩展资源、重启应用、回滚部署等。例如，Azure SRE Agent支持对Azure Kubernetes服务（AKS）的Pod重启和版本回滚。

• 安全与合规管理：持续审核资源是否符合安全实践（如TLS版本、托管身份启用），并自动修复漏洞。

• 开发者协作闭环：生成包含详细诊断信息的GitHub Issue，帮助开发者修复代码并防止问题复发。

3. 与传统SRE的差异

• 自主性与学习能力：AI代理通过知识图谱和多层级记忆管理积累系统上下文，逐步优化决策。例如，Cleric能通过历史事件推断Redis内存压力可能导致级联故障。

• 多工具协同：支持与Kubernetes、Datadog、Slack等平台集成，调用API执行跨系统操作。

• 实时性与规模：并行处理数千个信号，同时分析日志、指标和追踪数据，远超人工处理速度。

4. 典型应用场景

• 云服务管理：如微软Azure SRE Agent专为Azure资源设计，提供每日健康报告和自动化缓解措施。

• 混合环境优化：AgentSRE等方案支持跨多云和本地基础设施的统一监控与修复。

• 金融与高可用系统：在银行等高风险场景中，AI代理通过预测性维护减少宕机损失。

5. 挑战与限制

• 实时数据依赖：代理需持续获取最新系统状态，数据延迟可能导致误判。

• 信任建立：初期需人类审核关键操作（如资金交易），逐步扩大自治范围。

• 成本控制：大规模部署可能带来算力与存储开销，需平衡效率与资源消耗。

6. 未来方向

行业正从“辅助诊断”迈向“自主修复”，如Traversal等公司通过多代理协作将平均修复时间（MTTR）降低90%。同时，AI SRE框架逐渐扩展至安全、网络等领域，形成跨职能的智能运维生态。

SRE通过工程化重构了运维的底层逻辑，而AI SRE Agent进一步将其推向智能化与自动化。两者的结合不仅解决了规模与复杂度的瓶颈，更重新定义了可靠性管理的边界——从“稳定优先”到“预测自愈”，最终实现系统韧性的质变。AI SRE Agent代表了运维自动化向智能化演进的关键技术，通过AI驱动的决策与行动，显著提升系统可靠性并释放工程师生产力。

我自己读的第一本数学分析教材是这本《A Course of Pure Mathematics》，由数学家 G.H.Hardy 在一百多年前所写的教材。

当年我阅读这本书的时候，还是2005年的时候，对数学家的了解也不够，对 G.H.Hardy 本人也没有足够的了解，后来随着学习的深入，我才发现 G.H.Hardy（1877–1947）是20世纪最具影响力的数学家之一，以其在数论和分析学领域的贡献而闻名。他长期任教于剑桥大学，培养了许多杰出的数学家。哈代的著作以清晰和严谨著称，除了《纯数学教程》外，他还与李特尔伍德（J.E. Littlewood）合作发表了大量重要论文，并与印度数学家拉马努金（Srinivasa Ramanujan）建立了深厚的学术友谊。哈代的数学哲学强调纯粹数学的美学价值，他认为数学的真正意义在于其内在的优雅和逻辑的完美。《纯数学教程》不仅是一本教科书，更是一部数学思想的经典表达。它适合那些希望深入理解分析学基础的读者，无论是初学者还是有一定数学背景的学生，都能从中受益匪浅。

《纯数学教程》这本书以其严谨的逻辑结构、清晰的表述和对数学基础的深刻洞察而闻名，长期以来被视为分析学领域的标准教材之一。数学家哈代在书中系统地介绍了实数、函数、极限、连续性、微分和积分等核心概念，为读者奠定了坚实的数学基础。

主要章节与内容概述

1. 实数变量（Real Variables）
   第一章深入探讨了实数的性质，包括有理数与无理数的定义、实数连续性的概念以及戴德金分割（Dedekind’s Theorem）。哈代通过几何直观和严格的数学论证，展示了实数系统的完备性，并引入了极限和收敛的基本思想。
2. 函数（Functions of Real Variables）
   第二章讨论了函数的定义及其图形表示，包括多项式函数和有理函数。哈代详细解释了函数的连续性、单调性以及极值问题，并通过大量例子帮助读者理解函数的多样性和复杂性。
3. 复数（Complex Numbers）
   第三章介绍了复数的基本理论，包括复数的代数运算、几何表示（阿冈图）和德摩弗定理（De Moivre’s Theorem）。这一章为后续分析复数函数提供了必要的工具。
4. 极限（Limits of Functions of a Positive Integral Variable）
   第四章专注于数列极限的理论，包括收敛的定义、极限的性质以及无穷级数的求和。哈代通过严格的证明和丰富的例子，帮助读者掌握极限的核心思想。
5. 连续函数的极限（Limits of Functions of a Continuous Variable）
   第五章将极限的概念推广到连续函数，讨论了函数的连续性、间断点以及一致连续性的重要性。这一章还包含了海涅-博雷尔定理（Heine-Borel Theorem）的证明。
6. 导数与微分（Derivatives and Integrals）
   第六章和第七章分别介绍了微分和积分的基本理论。哈代详细阐述了导数的定义、求导法则以及微分的应用，随后转向积分的概念，包括黎曼积分的定义和基本性质。
7. 对数与指数函数（The Logarithmic and Exponential Functions）
   第八章专门讨论了对数函数和指数函数的性质，包括它们的级数展开和函数方程。哈代还涉及了三角函数和双曲函数，展示了这些函数在分析中的重要性。
8. 附录（Appendices）
   书的最后部分包含四个附录，分别讨论了方程的根的存在性、双重极限问题、圆函数的定义以及分析和几何中的无穷概念。这些附录为读者提供了更深入的数学背景和补充材料。

以第125小节的“中值定理”（The Mean Value Theorem）的内容，总结本书的特色：

• 以核心定理为纲：贯穿几何直观、严格证明与应用延伸；
• 注重逻辑严谨性：同时通过例题和注释培养读者的数学思维；
• 平衡经典与现代：既传承传统内容，又融入当时的最新观点，即使在一百年之后，这些观点依然有其深刻的意义。

1. 严谨的逻辑推导

• 定理陈述清晰：哈代明确提出了中值定理的核心内容：若函数  在区间  内可导，则存在  使得 
• 几何直观与严格证明结合：他先用几何意义（曲线弦与切线的平行性）直观解释定理，随后通过构造辅助函数并应用罗尔定理（Theorem B of §121）给出严格的解析证明，体现了从直观到形式化的过渡。参考 Fig.43。

2. 强调数学思想而非技巧

• 核心地位：哈代称中值定理为“微分学中最重要的定理”，凸显其核心地位，而非仅将其视为工具。
• 推广形式：定理被进一步表述为  便于后续应用（如泰勒展开的铺垫）。

3. 丰富的应用与延伸

• 例题引导思考：章节末尾的习题设计巧妙，例如：

1. 验证定理对  和  的成立性；
2. 利用中值定理证明函数在导数为零的区间内为常数；
3. 推广到复合函数求导法则（链式法则）的证明。

4. 语言风格与教学理念

• 简洁而深刻：哈代的叙述简洁直接，但每一句话都蕴含关键信息。例如，他指出定理的几何意义“无需严格证明”，但依然给出完整解析证明，体现对严谨性的追求。
• 启发式教学：通过问题引导读者自主探索（如习题中要求验证特殊情形），符合他倡导的“数学是创造性活动”的理念。题目中大量来自 Math. Trip 的习题，很有特点。

作为一名数学系的本科生，如何高效地整理和吸收数学知识、深化理论理解，是每个学生都会面临的挑战。知乎直答，这一结合了知乎平台丰富内容和强大AI大模型的工具，提供了一个可以极大助力学习的数字化助手。通过智能搜索、结构化答案生成、实时信息更新和个性化创作等功能，知乎直答能够帮助你在数学学习中快速建立知识体系，提升理解深度，并且通过互动式的学习模式帮助你掌握复杂概念。

知乎直答能够帮助你高效构建个人数学知识库。作为数学学生，你会接触大量的抽象定理和复杂公式。通过知乎直答的智能精准搜索功能，你可以快速检索到与特定概念相关的高质量答案，无论是经典的数学分析定理，还是现代的高维几何理论。知乎直答不仅支持从知乎问答中提取相关知识，还能结合权威百科和学术论文等外部数据源，确保你获得的信息准确且全面。例如，在学习“拉格朗日乘数法”时，你可以输入相关问题，知乎直答会自动给出详细的定理解释、公式推导过程，甚至包含了该方法的应用实例。

接下来，知乎直答的结构化答案生成功能将帮助你整理和归纳数学知识。数学的学习往往不是零散的，而是一个不断拓展和加深的过程。知乎直答会根据问题的性质，将答案按“背景-核心-分析-总结”的结构组织起来，帮助你系统化地理解问题。例如，如果你提问“什么是傅里叶变换”，知乎直答不仅会给出傅里叶变换的定义，还会解释其背景、推导过程以及如何在实际中应用，最后提供一些总结性的学习要点。这样的结构化呈现能够帮助你更容易地消化和记忆复杂的数学概念。

知乎直答的实时信息追踪功能能够让你保持与数学前沿研究的同步。在数学的学习过程中，你不仅仅是学习课本知识，更要关注学科的最新动态。例如，当你学习“数学中的非欧几何”时，知乎直答可以通过实时更新，给你展示这一领域的最新研究成果和相关学术讨论。这使得你能够深入了解理论发展和应用实例，拓宽自己的知识面。

知乎直答的个性化创作助手也是你数学学习中的得力助手。它可以帮助你撰写数学报告、生成数学问题的推导过程，甚至设计学习计划和复习提纲。例如，在准备期末考试时，你可以让知乎直答根据各门课程的知识点生成思维导图，帮助你梳理考试复习的重点。对于数学公式的排版，知乎直答还可以利用LaTeX进行高质量的公式排版，使得整个学习过程更加专业和清晰。

一个很重要的优势是，知乎直答支持多轮对话，这使得你可以深入挖掘数学问题的各个方面。比如，你可以先提问“什么是微分方程”，得到基础解答后，再继续追问“常微分方程的稳定性分析方法”。知乎直答会根据上下文继续跟进，为你提供层层深入的解答，帮助你逐步掌握复杂的数学概念和方法。这种多轮对话的形式非常适合数学学习，因为数学的理解往往需要层层递进，而知乎直答正好能为你提供这样的学习模式。

在实际应用中，知乎直答还能帮助你高效整理和提炼学术资源。如果你有大量的数学文献需要阅读，知乎直答的文档解析功能可以快速从论文、书籍、讲义中提炼出最关键的信息。例如，你可以上传一篇关于“数学分析”或“复分析”的学术论文，知乎直答会帮助你提取出核心定理和方法，并根据你的需要整理成简洁的要点或思维导图。

学习方法与知乎直答的结合不仅仅限于对个别知识点的理解。你可以将知乎直答作为一种长期的学习工具，构建自己的个人数学知识库。在日常学习中，每当遇到不懂的概念或定理时，直接通过知乎直答进行提问，及时获取权威且详细的解答。同时，通过多轮对话深入探讨该概念的不同角度，进行全面的理解。你还可以通过知乎直答记录自己的学习笔记，并将其转化为结构化的内容，方便日后的复习和查阅。

知乎直答为数学系学生提供了一个高效、精准且个性化的学习平台，通过智能搜索、结构化呈现、实时更新以及创作助手等多种功能，帮助你在数学学习的道路上事半功倍。通过知乎直答，你不仅能够更好地理解课程中的理论，还能及时掌握数学领域的前沿动态，真正实现学习过程中的自我提升和知识积累。

在如今的信息化时代，团队的竞争力往往与其工作效率密切相关。无论是跨部门协作、知识管理，还是技术问题的快速解决，都离不开高效的信息流转和沟通。而在某些团队中，重复性工作、低效的沟通流程和技术支持问题，常常成为员工在日常工作中遇到的痛点。随着智能化工具的崛起，IMA（智能管理助手）作为一款强大的知识管理和智能协作工具，正在逐渐成为小规模团队提升工作效率、优化流程的必备利器。今天，我们将通过几个典型的应用场景，详细阐述IMA如何帮助小规模团队解决工作中的种种痛点，进而提高整体的运营效率。

建立专项知识库，解决流程中的痛点

在某些团队中，员工在完成日常工作时，经常需要反复提交相同的材料，或是在跨部门的审批过程中因流程不清晰、信息沟通不畅而浪费大量时间。尤其是在大型项目中，Aspice文档的撰写、标书的撰写、与供应商的沟通、审批流程的走查和反馈常常需要大量人工干预，这不仅效率低下，而且容易出错。

为了帮助大家在工作中解决这一问题，IMA系统提供了一个非常有效的解决方案。通过建立「标书模板库」和「跨部门协作流程库」，团队可以将常见的报告模板、审批流程标准化文档以及操作指南存入IMA的知识库。这些文件一旦存储后，员工可以通过IMA的智能检索功能，轻松找到所需资料。例如，当员工需要准备某类报告或是跟进专利审批时，只需要在IMA中输入关键词（如“专利审批流程”），系统便会自动为其展示最新的操作指南和文档。这样，员工不仅避免了重复的沟通，还能够在最短的时间内找到最准确的资料，大大提高了工作效率。

通过这种方式，团队能够实现流程的标准化管理，减少了低效的材料提交和流程咨询。据实际案例显示，使用IMA后，标书撰写的时间可大量缩短，审批流程的沟通效率也得到了显著提升。

自动化信息整合，打破信息孤岛

在某些团队中，由于外部信息获取渠道不畅通，常常面临“信息孤岛”的困境。尤其是在一些条件较为限制的工作环境中，员工在面临技术问题时，无法及时获取行业最新动态或技术信息，这不仅影响工作进度，还容易错过行业发展的重要趋势。

IMA系统通过其强大的网页抓取功能和浏览器插件，能够采集并存储外部行业的最新技术动态。无论是汽车技术、电池技术、AI算法，还是其他领域的前沿研究，IMA都能通过联网功能和插件抓取并存储更新到「外部技术监测」知识库中。这种自动化的信息整合方式，不仅解决了信息孤岛的问题，还使得员工始终保持对行业最新发展的敏感度，有效避免了技术滞后。

通过IMA的这一功能，技术团队能够更快地了解行业的最新发展，帮助团队成员时刻保持竞争优势。而员工不再因为信息滞后而焦虑，也能够专注于更具创造性和价值的工作。

智能协作，减少无效会议

某些企业和团队中的会议往往是时间浪费的重灾区，许多会议缺乏明确的议题和目标，参与者未能事先了解讨论的核心问题，会议内容往往散漫无序，结果无论是会议结束后的落实，还是与会者的反馈，都难以达到预期效果。而由于大量无效会议占用了员工宝贵的工作时间，整体的工作效率显著下降。

在这个问题上，IMA通过智能化的协作功能，帮助团队大幅减少了低效会议的数量。在会议前，员工可以基于PDF、PPTX、Word、Excel等文档资料，通过IMA知识库快速生成会议提纲，系统会根据输入的议题自动输出讨论框架，确保会议内容紧密围绕核心目标展开，并且使用笔记进行共享记录。在会议进行过程中，IMA还能够通过笔记这个功能实时记录讨论内容，并且整理成会议纪要，并在会议结束后，人工导入知识库并确保每个任务都有落实和跟进，以便下次开会进行沟通和跟进。

这种智能化的会议管理方式有效避免了无主题、无效沟通的情况发生。通过IMA的协作功能，团队能够实现高效的会议管理，避免员工在低效会议中浪费时间，从而提升工作整体效率。

技术问题即时响应，替代加班

开发人员常常面临各种技术问题，尤其是在工具链出现问题或系统出现报错时，开发人员往往需要加班处理，这不仅影响工作进度，也损害了员工的工作与生活平衡。传统的技术支持模式往往需要较长时间的等待和反复沟通，而加班成为解决问题的常态。

团队的员工可以基于IMA系统建立「内部技术问答库」，收录常见的技术问题和解决方案，如各种软件工具的故障排除、报错日志的分析等。通过IMA的代码解析功能，员工只需将报错日志输入系统，IMA就会迅速给出可能的修复方案，帮助员工第一时间解决技术问题。通过这种即时响应机制，技术人员不仅能够迅速解决问题，还能避免不必要的加班。

通过IMA，团队的员工能够有效提高技术支持的效率，减少因技术问题造成的加班，提升员工的工作体验，同时也确保了开发进度不受阻碍。

结束语

总的来说，IMA系统为大家提供了一整套高效的知识管理与智能协作解决方案，通过智能化的流程优化、自动化的信息整合、精细化的绩效管理以及技术问题的即时响应，帮助团队里面的减少重复性工作，提高工作效率，并为员工提供了更舒适、高效的工作环境。在信息化和智能化的浪潮下，IMA作为一款高效的管理工具，无疑为团队的未来发展提供了强大的动力。

在某家公司，管理制度几乎完全建立在“罚”之上。从员工的衣着、在工位使用手机的频率，到工位绿植是否黄叶、走在路上是否玩手机、办公室的整洁程度，甚至连PPT是否字多都成为了处罚对象。表面上看，这似乎是为了“提高标准、规范行为”，实则是管理失能的体现——用“罚”代替了真正的管理。

本质上，这种“以罚代管”并不是管理，而是企业的一种偷懒。管理者不去分析行为背后的原因，不建立明确的标准和持续优化的流程，而是通过简单粗暴的经济惩罚转嫁责任。当绿萝发黄不是提醒后更换，而是直接对员工进行罚款；当PPT内容太多不是优化表达方式，而是计罚金处理，最终形成的是一个“员工时刻提心吊胆、效率却不升反降”的畸形组织氛围。

更严重的是，这种制度传递的信号是：“公司不相信员工，只相信罚款。”本应建立在信任与激励之上的团队文化，变成了“管你不是为了成长，是为了你别犯错”的低信任环境。员工每天关注的不是如何提升工作质量，而是“今天有没有被抓到哪里没达标”，长此以往，创新会被遏制，热情会被磨平，企业发展也会停滞。“罚款式管理”往往激励错位。某些主管可能为了完成所谓的“执行力指标”或“管理考核”，对下属进行密集式处罚，使得原本用于指导和辅导的角色变成了“罚款机器”。在日常的工作安排和沟通中，某些主管也会说“做不完就处罚你”之类的话语，员工就出现了“多做多错、少做少错、不做不错”的怪圈。在这样的文化中，谁还敢表达真实想法？谁还愿意主动承担责任？公司变得越来越安静，但不是因为稳定，而是因为压抑。

最令人担忧的是，这种管理方式极易引发员工反感甚至流失。管理制度本该是团队共同达成目标的管理工具，却演变成了对员工的“狩猎工具”。当员工把企业看作“监工型压榨者”而非“发展平台”，员工的离职只会越来越频繁，留存的也只是麻木不仁或毫无选择的人。

“以罚代管”不是企业管理的现代化，而是管理者懒政的代名词。真正有责任、有远见的管理，是通过激励机制、制度完善和人性化引导，构建有温度、有秩序的职场生态。任何脱离理解和沟通、只靠罚款驱动的管理，终将失去人心，败于文化。

《回乡偶书》
贺知章
少小离家老大回，乡音无改鬓毛衰。
儿童相见不相识，笑问客从何处来。

2005年，我从贵州考上大学，离开了那片山水。从此，人生的脚步逐渐向外延伸，求学、工作、成家……生活的重心慢慢远离故乡，纵使节假日偶有归途，也只是匆匆一瞥，再难真正走入家乡的深处。

二十年后，我因公司的团建活动，再一次踏上贵州的土地。这一次，却不是归家探亲，而是以一名“旅人”的身份，回望那个曾经熟悉得闭着眼都能画出轮廓的地方。那一刻，我忽然想起杜甫的那句诗：“少小离家老大回，乡音无改鬓毛衰。儿童相见不相识，笑问客从何处来。”

是的，故乡还在，但我仿佛已成了它的客人。

这次旅行，我们从深圳出发，坐高铁抵达贵阳。六天的行程，走过了贵州博物馆、西江千户苗寨、黄果树瀑布、天星桥、陡坡塘瀑布、万峰林……这些景点，过去对我来说既近又远。除了黄果树瀑布，那还是我少年时随家人游览的地方，其余皆为初见。印象中，那时的黄果树还没有如今的扶梯直上直下，游人要亲自沿石阶上下，脚步虽累，却也踏实。那时候，也没有智能手机，照片只能在景区设立的拍照点匆匆留影，如今随手举起手机就能定格风景，但那时的留念似乎更具仪式感。

西江的苗寨在晨雾中沉静古老，万峰林的轮廓如刀刻般耸立，我在这些景色里游走，既像游客，又像回忆的行者。童年的贵州并不富庶，生活也简单朴素，而今所见所闻却早已焕然一新。我一边感叹它的变化，一边也默默感受着一种难以言说的疏离感——我似乎不再属于它，但它却始终是我心中难以抹去的一部分。

故乡，从未真正离开，但在时间的风中，我们都悄悄改变了模样。这次旅程，不只是一次旅行，更像是一次温柔而略带惆怅的自我追问——我从哪里来，我又将归于何处。

记忆里的贵州，总是潮湿的。正所谓“天无三日晴，地无三尺平”。小时候只要离开城市，就能看到高速公路的两边是稻田，远处是雾气缭绕的山岭。那时候的日子慢，读书、写作业、打篮球——那是我记忆中最真实的童年。

而如今再回到这里，一切熟悉又陌生。那些低矮的瓦房多半已不见，替代的是一幢幢新修的旅店和游客接待点；曾经的小道被铺上了水泥砖。我努力地在这些变化中寻找一点旧日的回声，却发现，那些属于童年的细节，或许早已无处可寻。很多画面浮现在脑海，又慢慢散去——曾经熟悉的人，有的还在，有的已离去；曾经熟悉的景，有的更新，有的消失。人终究无法两次踏进同一条河流，更无法回到那个无忧的年代。

这次团建之行看似是一次简单的旅行，实则像是一场跨越二十年的回声对话。在繁华与喧嚣的景区里，我仿佛听见自己小时候的笑声，渐渐远去，最后只剩风声轻响。

贵州，二十年后再见。山川依旧，云烟仍浓，而我，早已不是那个离开的孩子了。

来源：Zheng Sullivan 知乎

黑科技，还是要提 D.E.Shaw Research 这个奇异的存在。

要讲这个黑科技，我们可能要扯远一点，先讲讲 D.E. Shaw 这个人是怎么学术赚钱通吃，成为彻底的人生大赢家的。

D.E.Shaw 是个学霸，是 PhD 们的偶像：斯坦福大学计算机专业的博士, 30 岁不到就进入哥伦比亚大学做教授，专门研究超大规模并行计算。这已经是优秀的学术人生了。

但是 Shaw 觉得无聊。哥伦比亚大学地处纽约，遍地暴发的对冲基金男各种花天酒地，游嬉于各种 model 之间，作为一个同样聪明的教授，却只能坐在冷板凳上写计算机 model。虽然在科学家眼里，后者甚至还要更性感一些，但是时间长了也……扯远了，总之，Shaw 不干了。

于是他 1986 年放弃了钻牛角尖的教授生涯，进入华尔街著名投行摩根士丹利做 quant trading（可以通俗地理解为用计算机自动炒股、债和外汇）。果然， 呆博士不是搞政治斗争的料子，在摩根斯坦利这种钱多是非多、政治斗争和技术斗争同样激烈的地方，仅仅 2 年之后他就在政治斗争中失败，被迫离开摩根斯坦利（欢迎 quant trading 方面的达人来八卦补全这一段故事）。但是这厮本来就不是池中物，同年，他就开办了自己的对冲基金 D.E. Shaw & Co. LP.，专注 quant trading，利用高速计算机网络和市场瞬间的有效性缺陷来进行高频统计套利。

和今天高频交易人满为患的情况不同：当时计算机很破，内存上兆的就是中型服务器了，计算机语言和组件也比较晦涩，不像今天这么普及和丰富，不会冒出来个 12 岁少年就能写一个网站编一个游戏，然后对着 80 后的老头子们说你们不行之类的。因此，能掌握高速网络编程和大型并行计算的人，除了能算弹道和模拟核爆之外，还能成为第一批做高频交易的人，干的事情基本就是无风险套利——利用市场无效性，剪市场的羊毛，赚钱的速度仅仅取决于你能剪多快。

作为专门研究超大规模并行计算的顶级专家的 Shaw，率先杀入高频交易，完全是流氓会武术，谁也挡不住，剪羊毛速度世界一流，很快人生进入了新的高峰。到 2015 年，他的个人净值已经 41 亿美元（David Shaw – Forbes），杀入全球财富榜前 500.

说了这么多，怎么还没有谈到计算化学？你别走，我现在就要说这事了。

David Shaw 大叔 40 出头财务自由，依照常人的想法，自然可以不再写 model，而一头扎进纽约的花天酒地，去约会真的 model 了。但是，正如网络上著名的牛顿生平文章《牛逼顿》所说：

出乎世俗想象的是，科学其实远比任何娘们儿都风骚，玩科学比玩女人爽得多，得到一个成果所获得的高潮强烈而持久，不仅有快感，更有巨大的自我认同感，远胜于那几秒寒颤之后无边的空虚与落寞。所以陈景润其实是沉溺于美色不能自拔，身体弱架不住高潮过度被爽死了。

Geek 的基因在身体深处摇撼 Shaw 大爷功成名就之后的空虚神经。他一个回马枪杀回了科学世界，脱下西装，露出了 Geek 的本色：

和屌丝 geek Sheldon 不一样，这是一个破坏力惊人的土豪 geek。Shaw 现在再也不用跪舔 NIH，NSF 的官员，去讨一点可怜的科研经费了。他想干什么就干什么；他觉得什么是前沿什么就是前沿。他拿出大规模并行计算的大砍刀，想找一个最需要计算但现今最不给力的领域一刀砍下去。

这里有个背景：计算化学发展了很多年，都处在有点尴尬的位置，说得直白点——计算机还太弱，计算化学用于实际问题中算不准，精度还不如做实验。因此，无论在化学还是生物领域，做计算化学的不管是教授还是 PhD，要么选择和实验的组合作，活在鄙视链的下游，要么躲到角落里小富即安地画圈圈。

因此，Shaw 的大砍刀就落到了萎靡的计算化学上：他想制造一台专门用于做计算化学的超级计算机，比现有的超级计算机强大几千倍几万倍。

很多人可能要问，现在超级计算机动辄就是几十万个 cpu 核心什么的，运算能力很强大啊，为什么还要造计算化学的超级计算机呢？

答案是，一般的计算机是很聪明，但是不适合干计算化学这行。学术一点说，是 general purpose computing 不能高效地来做分子动力学模拟。

打个比方，现在的电脑就仿佛是个全能的机器人，你可以让他去割麦子，做饭，踢球等等。让他去干很多事情，他什么都能干，干得也比人快，确实也很聪明。这就是所谓的通用计算机（general purpose computing）：一个机器，写不同的软件，实现各种功能。

但是在割麦子这件事情上，这个全能机器人的速度很难超越专业的大型联合收割机。因为大型联合收割机虽然笨，但是完全为割麦子而生，因此硬件上量身定制，极度优化。这就是所谓的特种计算机（special purpose computing）：专业定制机器，软件也是专门定制的，只实现一个功能，但是凶残而高效。

Shaw 就是要造一台计算化学中的“大型联合收割机”。这台收割机，叫做 Anton。

它很贵很贵，但这正是 Shaw 的优势，反正他不泡妞不包二奶，钱花不完。况且，科研人员其实很便宜。

这里有一个好笑又辛酸的事情：和大众的认识恰好相反，在美国，纯理科博士毕业之后大多数都找不到工作，虽然智商大都不低，但是如果想坚持科研，做博士后的薪水只能勉强维持生活。

而 David Shaw 横空出世，成为了纽约的孟尝君。他招了一群找不到工作的博士——这些人在经济上可以说是纯粹的屌丝——开出了 10 万美元一年的工资。

10 万美元一年是什么概念呢？这就是投资银行 21、2 岁小分析员的入门工资 + 奖金，在华尔街上就是底层，外面穿着西装，里面穿的可是开裆裤。但是对于这帮年届三十的科学屌丝来说，这是他们能找到研究岗位工资的 2-3 倍，是个做梦都想不到的包养价。

于是一时间最顶尖的计算化学、生物物理、电子工程博士趋之若鹜，求 David Shaw 包养。

从 2004 年前后开始（请知情人指正），Shaw 成立的 DE Shaw Research（DESRES）开始正式运营。在 David Shaw 的精心包养下，30 多个失业的博士屌丝们什么也没干，在优雅的环境里，足足读了一年半的论文，搞出了 Anton 的草图。之后，更多的屌丝加入，全身心专注于 Anton 的研发。

2007 年，比预期还早了快一年，来自五湖四海的屌丝和 geek 们发布了 Anton 的第一代。计算化学的最大黑科技诞生了：它比一般的超级计算机快约 10,000 倍。比最好的超算也快 1,000 倍。

对的。变态的 10,000 倍，四个零，四个数量级。

10000 倍是什么意思呢？计算化学里面，模拟分子运动轨迹的持续时间的长短是非常重要的。用模拟网球比赛来做类比：以前“超级计算机”算了一个月，我们只能模拟出击球的 1 秒钟的瞬间，而现在 Anton 出世，我们同样花一个月，就可以模拟整场球赛中网球的轨迹了。

这是前所未有的超算能力，变态的“大型联合收割机”，等于开了上帝视角啊亲。

从 2007 年起，D.E. Shaw 的团队声名鹊起，用这个收割机每年在国际顶尖的学术杂志《自然》和《科学》上灌水，学术声誉不可阻挡。Anton 在手，高枕无忧，仿佛别人在地面用卷尺画地图，他们在天上航拍做地图。现在他们又出了 Anton2，继续吊打“过去 8 年中取得了长足发展的”超级计算机。

也许纯学术派对这种硬拼计算能力的方法表示不屑，但 D.E. Shaw 和他包养的 geek 们正用变态的 Anton 计算机把分子动力学模拟大跨步地推向实用。

有钱就是任性。

希望有更多的科学家出现，也希望有更多类似D.E.Shaw这样的土豪科学家用黑科技摧枯拉朽地带动科学前进。

百年数学难题的终极突破：Kakeya猜想的三维解答

在数学的浩瀚宇宙中，许多看似简单的问题背后都暗藏玄机，令人琢磨不透。1917年，日本数学家挂谷宗一（Soichi Kakeya）提出的一个几何问题，乍看之下或许不以为意，但却开启了一个跨越百年的数学探索之旅。问题的核心是：“在平面上旋转一根单位长度的针，所需的最小面积是多少？”这个问题，后来被称为挂谷转针问题（Kakeya needle problem），而它背后的挑战则是现代几何测度论中的一个深刻谜题——挂谷猜想（Kakeya conjecture）。

 从旋转针尖到数学革命

经典答案的颠覆

初期，数学家们认为，最小面积应由等边三角形（面积约0.577）或三尖点内摆线（面积0.392）实现。然而，在1928年，俄裔数学家贝西科维奇（Abram Besicovitch）提出了令人震惊的构造，证明了存在一种名为“贝西科维奇集”（Besicovitch set）的几何形状，它能够在几乎任意小的面积内容纳所有方向的单位线段。这个看似反直觉的结论的核心是“帕尔连接”（Pal join）技巧，通过平移和重叠三角形切片，极限压缩面积至几乎为零。

维度之谜的浮现

随着时间的推移，数学家的目光从面积转向了维度的谜题。1971年，罗伊·戴维斯（Roy Davies）证明了二维空间中的贝西科维奇集的豪斯多夫维度必须为2，意味着在平面上，包含所有方向单位线段的集合必须填满整个平面。然而，问题在三维空间中变得更加复杂。挂谷猜想的核心命题问的是：如果一个集合包含所有方向的单位线段，那么在三维空间中，它的维度是否必然为3？这个问题困扰了世界顶尖数学家近50年，甚至包括陶哲轩等人。

三维突破：王虹与Zahl的世纪性证明

终于，2025年2月，纽约大学的王虹和英属哥伦比亚大学的Joshua Zahl发布了一篇128页的预印本论文，彻底解决了三维挂谷猜想的问题。

定理：三维空间中的任何挂谷集，其豪斯多夫维数与闵可夫斯基维数均为3。

这意味着，无论如何精巧构造，三维空间中“容纳所有方向线段的集合”必须占据满维空间，无法被无限压缩。这个突破性的结果被誉为“世纪性成果”，解决了几何测度论中的核心难题，并为相关数学领域提供了新的思路。

证明的核心创新

粘性集合（Sticky Kakeya sets）：

王虹与Zahl的研究首先集中在一个全新的概念上——粘性集合。他们提出，如果挂谷集在多个尺度上展现出“自相似粘性”（即细管高度聚集于粗管），那么其维度必为3。这一发现成为解决问题的关键之一。

多尺度归纳法：

在研究过程中，王虹与Zahl通过递归分析不同尺度下管状结构的“密度阈值”，成功将非粘性情况转化为粘性框架，最终得出了正确的结论。他们的研究突破了传统方法的限制，运用了代数几何与组合技术，尤其是多项式方法和投影几何技术，有效突破了过去几十年数学家的思维束缚。

为何三维如此艰难？

尽管二维问题已经被解决，但三维空间的复杂性远远超出了预期。三维空间中的方向和旋转路径呈现出更加复杂的交错与重叠模式，这使得传统的贝西科维奇“面积压缩”技巧在三维中失效。即使是著名数学家沃尔夫（Thomas Wolff）在1995年提出的下界（维度≥2.5）也未能为解决问题提供突破。因此，王虹与Zahl的证明，可以说是在非常复杂的数学框架下取得的重大发现。

挂谷猜想的数学宇宙

挂谷猜想不仅仅是一个几何问题，它与多个数学领域密切相关，且有着深远的影响：

• 调和分析：傅里叶变换的限制猜想（Restriction conjecture）就需要依赖于挂谷猜想的基础。
• 流体力学：纳维-斯托克斯方程的解的奇点分析与挂谷集的结构相关。
• 数论与密码学：有限域上的挂谷集已被证明与伪随机数生成模型密切相关。

这些交织的领域，进一步展示了挂谷猜想在现代数学中的核心地位，表明它不仅仅是几何测度论中的一个难题，也为其他学科提供了重要的启发和应用。

未竟之旅：高维战场

尽管三维挂谷猜想已经被解决，但四维及以上的高维空间仍然是未知领域。数学家们推测，在n维空间中，挂谷集的维度应为n，但现有工具尚难处理高维代数簇的复杂性。王虹与Zahl的证明框架为高维推广提供了可能的路径，但高维战场依旧充满挑战。

数学史启示

挂谷猜想的百年历程正如数学家哈代所言：“真正的数学问题，其美感不因时间褪色，反因挑战而愈发璀璨。”这不仅是对数学家辛勤付出的致敬，也是对数学领域不断追求未知、探索极限的诠释。从针的旋转到空间的本质，挂谷猜想连接了分形几何、调和分析、数论等多个数学分支。三维的突破是数学史上的里程碑，而四维及以上的挑战则依旧未解，等待着未来数学家们继续探索。挂谷猜想的解决，正如数学家所言：“最优雅的问题，往往藏于最朴素的起点。”

Hardy 与 Littlewood 的合作堪称数学史上合作关系的典范。在他们合作的极盛时期，欧洲数学界流传着许多有关他们的善意玩笑。 比如 Bohr 曾经开玩笑说当时英国共有三位第一流的数学家：一位是 Hardy，一位是 Littlewood，还有一位是 Hardy-Littlewood。而与之截然相反的另一个玩笑则宣称 Littlewood 根本就不存在，是 Hardy 为了自己的文章一旦出现错误时可以有替罪羊而杜撰出来的虚拟人物。 据说 Landau 还专程从德国跑到英国来证实Littlewood 的存在性。

素数（如2, 3, 5, 7, 11, 13…）是只能被1和它本身整除的正整数，被称为“算术的原子”。

数学家长期试图理解：素数在数轴上是如何分布的？表面看，它们很随机，但又不是完全无序。素数，是算术的原子，也是数学的诗篇。书的开篇如游戏开场，“谁想成为百万富翁？”用一个富有现代气息的问题，把读者从功利的世界轻轻拉入一个古老、神秘的国度。素数之谜的诱人魅力不言自明，那些散布在数轴上的孤独整数，如恒星般璀璨，却从不规律地排列，仿佛宇宙中跳动的节奏，等待人类去探寻其中的和谐与隐秘的旋律。

黎曼猜想（Riemann Hypothesis）是数论中最著名、最深邃也最神秘的未解难题之一。它由德国数学家伯恩哈德·黎曼（Bernhard Riemann）于1859年提出，至今悬而未决，被称为“数学皇冠上的明珠”。其本质是关于素数分布的一个深层猜想。它指出：所有非平凡零点的实部都等于 1/2。我们分开来解释。

欧拉在18世纪发现了一个惊人的联系：正整数的幂次求和可以与素数的幂次乘积通过一个公式联系到一起，它把素数和函数论连接了起来。黎曼进一步研究这个函数，并将其延拓到复数域（复变函数），得到了一个具有非凡意义的观察：ζ 函数的“零点”，与素数的分布密切相关。

黎曼注意到 ζ(s) 在复数域中有无穷多个零点。去掉那些“平凡零点”后（即 s = -2, -4, -6, …），剩下的“非平凡零点”出现在所谓的“临界带”：黎曼猜想断言：所有非平凡零点的实部都是 1/2。也就是说，这些零点全都位于复平面上的“临界线”：Re(s)= \frac{1}{2}。

在《悠扬的素数》中，黎曼的身影几乎是全书的主线。他用虚数作为观察镜，发现素数在混乱中隐藏的节奏，仿佛宇宙的心跳。而后继者如：

希尔伯特曾说：“如果我死后能复生，第一件事就是问黎曼猜想是否已经被证明。”

阿塔拉·塞尔贝格、哈代与李特尔伍德、埃尔德什等名家也都为其贡献一砖一瓦。

蒙哥马利与戴森发现其零点分布与量子混沌系统相似，拉近数学与物理的边界。

在这个以快节奏和实用主义主导的时代，《悠扬的素数：只有勇者，才能够攀登数学的珠峰》如一股清泉，静静流淌，却激起无数涟漪。这本书，不仅是一部素数的朝圣之旅，更是献给所有热爱思考者的一曲深情咏叹调。20周年纪念增订版，让人重温数学之美，也见证人类在这座知识珠峰上的攀登轨迹。

作者用娓娓道来的笔触，将数学史上一道道闪光的名字编织成一幅宏伟的智者群像画。欧几里得的冷峻、欧拉的优雅、高斯的洞察、黎曼的深邃……他们不仅是定理的缔造者，更是精神世界的开拓者。尤其是黎曼，那位用虚数搭建观察镜、窥见另一个宇宙秩序的神秘数学家，他提出的黎曼假设，是本书贯穿始终的隐线，也是数学王国中最炽热的圣杯。

书中的语言轻盈而不轻薄，深刻而不晦涩。作者时而引用古典诗意：“ζ函数：音乐与数学的对白”，时而嵌入科技话题：“未来是光明的，未来是椭圆的”。每一章都有其节奏与情绪的变化，就像一场探险：从远古的演算石板，到量子鼓面上跳动的零点，从哥德尔的不完全性，到RSA的公钥密码，从虚数空间的镜中花，到大数据背景下寻找大素数的工程，这本书既是一部思想史，也是一部数学的交响诗。

在《悠扬的素数》中，黎曼 ζ 函数的零点被比作一场音乐会的“音符”，每一个零点都有其节奏。黎曼猜想就像乐谱中的和声要求——若它成立，那整个数学宇宙就会像一首完美的交响曲，充满秩序与美感；若它不成立，整个宇宙的“调性”都将改变。黎曼猜想，不仅是关于函数的技术问题，更是一面镜子，映出人类追寻秩序与美的勇气。它是数学中的“珠穆朗玛峰”，吸引着一代又一代的攀登者。无论我们是否登顶，它始终在那，用它神秘的姿态提醒我们：最伟大的问题，往往不仅关乎答案，更关乎追问本身。

在《悠扬的素数》中，作者将 Hardy 描述为“数学唯美主义者”，他追求的是无用之美。他曾以一种近乎狂热的信仰写道：“我从未做过一件对人类实用的事，这是我作为纯数学家的荣耀。”而 Littlewood，是比他年轻六岁的搭档。他不像 Hardy 那样“高冷”，更多一份幽默和实用精神。他们从1911年开始合作，持续了将近四十年，在素数、级数、ζ函数等领域合著了超过100篇论文。他们的合作之深，不仅体现在成果上，更体现在他们之间那四条著名的“数学合作守则”上：

1. 写给彼此的内容，对错并不重要；
2. 没有义务回信，甚至没有义务阅读对方的信件；
3. 尽可能不要思考同样的问题；
4. 每篇合著文章都视为共同作品，哪怕一方完全没参与。

这些幽默的条款，其实是对学术合作本质的深刻理解：信任、高度自治、责任共享与彼此照顾。在《悠扬的素数》的结构中，这正是数学精神的一部分：人类不是孤独地攀登这座珠峰，而是手牵手、肩并肩地在冰雪间前行。

书中没有详细展开 Hardy 和 Littlewood 的逸事，但他们的故事流传至今，仍如琴弦上的颤音，余音绕梁。最著名的，当然是 Hardy 去医院探望拉马努金时说的那个“出租车笑话”：

Hardy 说：“我坐的出租车号是 1729，好无趣的数字。”拉马努金马上答道：“不，那是一个非常有趣的数字！它是最小的可以用两种不同方式写成两个立方数之和的数：1729 = 1³ + 12³ = 9³ + 10³。”Littlewood 听说这个故事后笑着说：“这是个典型的 Hardy 式数学笑话：优雅、抽象、毫不实用。”

在数学的历史上，没有几对搭档像 Hardy 和 Littlewood 一样，留下如此深远的痕迹。他们没有破解黎曼假设，但他们拓展了通向它的路径。他们用分析的方法处理素数的分布，让原本“跳跃无序”的整数显出隐藏的节奏和韵律。

《悠扬的素数》不是纯粹讲数学理论的书，它讲的是人——执着的数学家、孤独的天才、沉默的计算者、突破常规的梦想家。而 Hardy 和 Littlewood，就像一对用数学谱曲的演奏家，在这部“素数交响曲”中演奏了最默契的一段二重奏。

尤为动人的是后记中，作者讲述张益唐与梅纳德关于素数间距的故事。这不仅是现代数学突破的真实记录，更是“孤独攀登者”精神的致敬。张益唐在清贫中坚持研究，梅纳德在工作中发现灵感，他们仿佛是黎曼在21世纪的回声：即使没有荣耀加身，即使无人喝彩，只要仍在为素数的秩序而燃烧，他们就是数学真正的英雄。《悠扬的素数》不只是一本数学书，它更像是一封写给智性之美的情书。读它的人，不必是数学家，但一定是爱思想、爱真理、爱自由的人。这本书教我们：在数字的荒原之中，依然可以听见诗歌，在冷峻的定理背后，也藏着人类最温热的梦想。

数学，作为一门基础学科，赋予了我们严谨的逻辑思维与强大的分析能力。这些优势不仅帮助我们解决数学问题，还能为我们打开多种职业大门。越来越多的数学与应用数学专业毕业生发现，凭借扎实的数学基础，他们能够顺利转行至金融、信息技术、教育等多个领域。本文将为你提供一份数学专业转行的全方位攻略，帮助你利用数学的核心优势，成功跨越行业壁垒，迈向更广阔的职业天地。

一、转行的可行性：数学是你的“万能钥匙”

基础学科优势：

数学不仅是自然科学的基础，它与金融、计算机、统计学等领域紧密相连。因此，数学与应用数学专业的学生在选择职业方向时，具有比其他专业更大的灵活性。数学专业与其他相关专业的联系将会更加紧密，报考该专业较之其他专业回旋余地大，重新择业改行也容易得多。

技能普适性：

数学的逻辑思维、建模能力和数据分析技能具有极强的跨行业适应性。无论你选择进入金融、信息技术，还是教育科研领域，数学专业所培养的分析思维和数据处理能力都能为你提供极大的职业竞争力。具备数学建模、数据分析能力的人才在金融、信息技术等领域需求旺盛。

二、主要转行方向：广阔天地任你行

1. 金融与数据分析

如果你对金融领域感兴趣，数学专业绝对是一个良好的起点。数学毕业生在金融领域的需求量大，尤其是在证券分析、风险管理、精算等岗位上，数学的建模与分析能力可充分发挥。证券分析师是理想方向之一，金融领域对数学人才需求广阔。

转型建议：补充金融知识，学习一些金融相关课程（如计量经济学、投资学等），以增强对金融市场的理解。学习编程语言，Python、R语言等编程工具已经成为金融数据分析和风险管理的标准工具，掌握这些工具将使你在转行时更具竞争力。

2. 信息技术（IT）

数学专业的学生非常适合从事IT行业的工作，如软件开发、算法设计、人工智能等领域。随着大数据和AI技术的兴起，数学的理论基础为这些领域的技术开发提供了坚实的支持。毕业生可在IT行业从事算法设计、大数据处理等工作。

转型建议：学习编程技能，掌握编程语言（如C++、Java）和数据结构，掌握算法设计的基本原理。参与技术项目，加入技术团队或参与开源项目，积累实战经验。

3. 教育与科研

如果你更倾向于回归学术，数学与应用数学专业的毕业生也可以选择成为中小学数学教师或高校研究人员。数学老师是主要职业选择，需考取教师资格证。

转型建议：考取教师资格证，如果你计划成为数学教师，参加相关的资格考试是必不可少的一步。继续深造，若你有兴趣从事科研工作，可以选择继续攻读硕士或博士学位，在数学或跨学科方向进行深入研究。

4. 公务员与企事业单位

数学专业的毕业生在政府机关及企事业单位中同样大有作为，尤其是在统计局、税务局等岗位上。

转型建议：考取相关证书，如统计师、金融分析师等证书，为进入公务员或企事业单位打下基础。参与相关实习，加入相关政府部门或企业进行实习，积累行业经验。

三、转行方法：如何有效跳槽？

1. 继续深造：拓宽职业视野

数学专业毕业生如果想跨行进入金融、IT等领域，继续深造是一个理想的选择。攻读金融工程、数据科学、计算机等硕士专业，不仅能够帮助你学习新领域的核心技能，还能提升你的行业认知。

深造建议：跨专业考研，导师往往青睐数学背景的学生，你可以选择攻读金融、计算机、数据科学等相关硕士专业，逐步提升自己在新领域的竞争力。参加在线课程，Coursera、edX等平台提供丰富的金融、编程等课程，利用空闲时间学习新技能。

2. 技能补充：线上学习与实践积累

在转行过程中，补充新领域的相关技能至关重要。通过参加在线课程和认证考试，你可以迅速提升自己在目标行业的竞争力。

技能提升建议：学习金融证书，如CFA（特许金融分析师）等金融证书，能够帮助你更好地进入金融领域。编程认证，学习Python、R语言等编程工具，参加相关认证考试，为进入IT行业打好基础。

3. 实习与项目经验：从实践中获得成长

实习和项目经验是转行的加分项。无论是进入金融公司、科技公司实习，还是参与数学建模竞赛、数据分析项目，都能为你提供宝贵的实践经验。

实习建议：金融/科技公司实习，尽早进入目标行业的公司实习，了解行业动态，积累实战经验。参与数学建模竞赛，如“全国大学生数学建模竞赛”等，通过竞赛积累实践经验，提升你的跨行业能力。

四、总结：数学专业的跨行之路，指日可待

数学作为一门基础学科，不仅培养了我们的抽象思维、严密逻辑和精准分析能力，还使我们具备了跨行业转型的独特优势。从金融到IT，从教育到公务员，数学专业毕业生的转行空间广阔，前景明亮。只要你针对性地补充相关领域的知识和技能，转行将变得轻松而顺利。结合个人兴趣与行业需求，制定合理的转行路径，未来的职业生涯将更加多元且充满可能。

数学是你通向未来的一把钥匙，走出舒适区，去探索更广阔的职业世界吧！

数学专业作为一门基础学科，不仅为学生提供了坚实的理论基础，还为日后的职业生涯提供了广阔的发展空间。随着数学与金融、计算机、数据科学等领域的紧密结合，越来越多的数学专业学生选择出国深造，提升自己的国际竞争力。本文将从留学前景、所学课程、就业与深造选择等方面，为你详细解析数学类专业的留学前景，助你规划未来的学术与职业发展。

一、留学前景：留学机会多，名校录取率高

深造比例与名校录取

数学类专业的留学前景非常广阔，特别是对于那些顶尖高校的毕业生。头部知名院校的数学类毕业生出国深造的比例大约为30%-50%。这些毕业生主要选择进入全球顶尖院校，如耶鲁大学、哥伦比亚大学、牛津大学、新加坡国立大学等，攻读数学、统计学、计算机或金融工程方向的硕士或博士学位。

特色留学项目

除了常规的出国深造路径，一些高校也提供了与海外院校合作的特色项目。例如某些高校会提供提供“2+2”或“3+1”的中外合作模式，学生可以在完成一定学业后，赴海外院校继续攻读硕士，获得双学位。

科研导向

对于有志于科研的学生，很多高校鼓励学生参与国际科研项目，这些项目为学生申请海外博士学位提供了良好的科研背景和实践经验。

二、所学专业核心内容：扎实的数学基础与广泛的应用

数学类专业的课程设置通常围绕数学核心知识展开，学生在掌握基本的数学技能的同时，还能够接触到许多跨学科的应用课程。

基础课程

数学核心课程：包括数学分析、高等代数、解析几何、概率论、实变函数、常微分方程、泛函分析等。

计算机技能：Python、C++程序设计，数据结构，数值分析，数学软件（如MATLAB、R语言）等，帮助学生掌握现代数学工具，为后续的应用打下基础。

特色方向课程

不同院校的数学类专业根据自身特色，开设了一些方向性的课程，帮助学生在特定领域内深耕：

金融数学：金融工程、风险管理、精算学、计量经济学等课程，以培养学生在金融行业中的应用能力。

数据科学：大数据分析、机器学习、数据挖掘、统计建模等课程，帮助学生在信息技术和大数据行业中发展。

数学教育：数学教学论、教育心理学、教材教法等课程，培养学生的教育能力，适合有意从事教学的学生，代表院校是各类师范大学。

应用数学：数学建模、运筹学、优化算法、计算几何等课程，培养学生的工程应用能力。

三、就业与深造选择：广阔的选择，充足的机会

国内升学

数学类专业的毕业生，尤其是成绩优秀的学生，通常有很大的机会保研或考研至国内顶尖院校，约40%-60%的毕业生选择继续深造。考研方向一般包括基础数学、计算机、经济学、金融工程等领域，很多学生成功进入清华、北大、复旦、交大等名校。

海外深造

基础学科：数学、统计学方向的博士学位通常具备较高的奖学金机会，数学类专业的博士生录取率较高。

应用方向：金融数学、数据科学等方向的硕士学位是热门选择，许多数学专业的毕业生成功获得北美名校的录取，并在就业市场上具备较强的竞争力。

直接就业

数学专业的毕业生不仅有良好的深造机会，直接进入职场也十分有利。根据专业方向的不同，毕业生可以选择以下岗位：

教育与科研：可从事中小学数学教师（需要教师资格证）或高校研究员（需博士学位）等工作。

金融与科技：量化分析师、数据科学家、精算师等热门岗位，薪资优厚，发展空间广阔。

四、院校专业特色对比：如何选择适合你的院校和专业？

根据不同院校的特色，数学类专业的学生可以根据自己的兴趣和职业规划选择合适的院校：

综合顶尖高校：头部学校院校具有强大的理论基础和科研导向，留学率超30%。适合那些有志于从事学术研究和深造的学生。

理工类强校：侧重于数学的交叉应用，尤其在人工智能、金融等领域的校企合作紧密，适合注重实际应用和技术发展的学生。

财经类院校：金融数学专业突出，具备丰富的就业资源和实践机会，适合有志于金融行业的学生。

师范类院校：具有强大的数学教育背景，适合从事基础教育的学生。

五、总结：数学专业的留学前景广阔，前途无限

数学类专业的留学前景非常广阔，特别是在金融数学、数据科学等应用方向，数学类专业的毕业生非常容易获得海外名校的录取。课程设置紧跟行业发展，除了提供坚实的数学基础外，还涵盖了金融、计算机、统计学等多个交叉学科领域。学生可以根据自己的兴趣和职业规划，选择适合的院校和专业方向，为未来的职业生涯奠定坚实的基础。无论是继续深造，还是直接就业，数学专业的学生都能在全球范围内找到属于自己的广阔舞台。

数学学科，作为基础学科之一，一直以来都被视为各行各业的“基础性武器”。随着时代的进步，数学不仅在传统领域占据重要地位，还在金融、信息技术、人工智能等新兴领域中展现了其巨大的应用价值。今天，我们将详细解析数学相关专业的就业前景，从就业领域、薪资水平到深造路径，为你揭开未来的就业蓝图。

一、就业领域：广阔且多样

数学与应用数学专业

数学与应用数学专业的毕业生，依托扎实的数学基础和强大的建模能力，能够在多个行业中脱颖而出。主要就业领域包括：

1. 教育行业：可以成为中小学数学教师，或者进入高校从事教学与科研工作。随着教育改革和数学教育需求的提升，相关岗位供需平衡良好。
2. 科研机构：数学专业毕业生在科研领域大有可为，可以进入中国科学院大学、中国科学技术大学等科研机构，开展数学理论或应用研究。
3. 金融与经济领域：随着数据分析和量化金融的快速发展，银行、证券、保险等机构急需数据分析师、风险评估师、精算师等岗位人才。
4. 信息技术行业：数学在软件开发、算法设计、数据分析等领域同样占有一席之地。尤其是在大数据、人工智能等热门领域，数学专业的毕业生具备天然的优势。
5. 企业管理：数学专业的学生具备出色的逻辑思维与建模能力，在生产管理、数据建模、决策支持等岗位上也能够发挥重要作用。

信息与计算科学专业

信息与计算科学专业不仅继承了数学的严谨性，还深度融合了计算机科学，毕业生的就业领域更为广泛：

1. IT与互联网行业：软件开发工程师、系统架构师以及人工智能算法设计等岗位需求旺盛，毕业生可以进入知名科技公司和互联网公司。
2. 数据分析：随着大数据时代的到来，数据分析师、数据挖掘工程师成为高薪岗位，毕业生可以在互联网公司、金融机构、大型企业等多个领域找到合适的职位。
3. 金融科技：金融信息系统开发、量化交易等岗位，需要既具备数学背景，又能熟练掌握计算机技术的复合型人才。
4. 科研与教育：部分毕业生选择回归学术，进入高校或科研院所进行研究与教学工作，为国家的科研事业做出贡献。

金融数学/应用统计专业

金融数学作为金融与数学相结合的热门专业，毕业生的就业领域主要集中在金融行业及其相关领域：

1. 金融机构：金融分析师、投资顾问、风险管理师等岗位十分抢手，金融数学专业毕业生能够为各大金融机构提供专业的风险评估与数据分析服务。
2. 保险与精算：随着社会对风险管理的关注，保险精算师和风险评估岗位需求大增。数学专业的毕业生往往能够进入保险公司从事相关工作。
3. 政府部门：经济规划、统计分析与政策研究等岗位也成为数学毕业生的就业方向，尤其是在经济发展与数据政策分析日益重要的当下。

其他交叉方向

除了传统领域，数学专业的毕业生还可以在以下交叉领域找到合适的职业发展空间：

1. 工程与科技领域：数学建模、数值计算等工作在航空航天、机械工程、建筑等行业中得到广泛应用。
2. 生物信息与医疗：随着健康数据和生物统计的需求增加，数学专业毕业生进入医疗行业，分析医学数据，助力精准医疗。

二、薪资水平：前景可期，薪资渐增

数学专业的毕业生，其薪资水平通常较为可观，特别是在金融、IT和数据分析领域。具体来看：

教育与科研领域：中小学数学教师年薪一般为8-15万元，高校教师或科研人员的年薪在15-30万元之间，随着职称和科研项目的增多，薪资水平逐步提高。

金融与IT领域：

1. 初级数据分析师/软件开发工程师：年薪约为10-20万元，随着经验的积累和技能的提升，薪资会逐步上涨。
2. 金融分析师/精算师：年薪在20-50万元之间，顶尖人才（如华尔街的金融数学家）年薪甚至能突破百万。
3. 企业管理与咨询：在风险管理和数据分析岗位上，年薪通常在15-30万元，具体数字会根据行业及地区有所不同。

地区差异：在一线城市（如北上广深），薪资水平通常高于二三线城市，差距在30%-50%之间。大城市的行业机会更多，薪资水平相对较高。

三、深造路径：走向更高的学术殿堂

数学专业的深造路径丰富，既可以选择国内继续深造，也可以跨学科发展，甚至选择出国深造，开启国际化职业生涯。

国内深造：

数学相关专业：攻读基础数学、应用数学、计算数学、统计学等硕士/博士课程，如中国矿业大学、南开大学等高水平院校提供优秀的研究平台。

1. 跨学科方向：许多数学毕业生选择转向计算机科学、金融工程、数据科学、人工智能等方向，这些领域的跨学科结合为数学专业的学生提供了更多的职业机会。
2. 保研与考研：优秀的毕业生可以通过保研或考研进入985/211高校，如武汉大学、中山大学等，这也是许多数学学子的深造选择。

出国深造：

1. 热门国家：许多数学专业的毕业生选择赴美、英、澳、加、新加坡等国继续深造，攻读数学、金融数学、计算机科学等热门学位，知名院校如麻省理工学院、斯坦福大学、伦敦政治经济学院等都是理想的留学目的地。
2. 深造优势：出国深造不仅能提升科研能力，还能通过跨学科的学习，拓宽职业选择范围。数学的严谨训练为进入金融、计算机等热门行业提供了强大的竞争力。

总结：数学专业——广阔天地，前程无量

无论你是想深耕教育科研，还是进入金融、信息技术等高薪行业，数学专业都能为你提供强大的职业支持。从理论到应用，数学专业毕业生不仅具备扎实的知识基础，还能够将数学工具灵活运用到各个领域，满足社会日益增长的需求。随着科技与经济的飞速发展，数学专业的就业前景只会越来越广阔。如果你对数学充满热情，不妨考虑将其作为未来职业的跳板，开创属于自己的精彩人生。

在国内高校中，数学科学学院一直以来都以其深厚的理论基础和广泛的应用方向吸引着大批优秀学子。从数学与应用数学到交叉学科专业，数学类专业的发展越来越注重理论与实践的结合，尤其是在大数据、金融科技和人工智能等热门领域，数学专业的就业前景持续看好。今天，我们就来一探全国高校数学科学学院的专业设置、课程安排和就业前景，为有志报考的考生们提供一份清晰的指南。

一、专业设置

数学科学学院的核心专业主要包括：

数学与应用数学：这是最传统的数学专业，注重培养具备扎实数学理论基础和强大应用能力的复合型人才。课程设置侧重数学建模与实际问题解决，培养学生在各类复杂问题中运用数学工具的能力。

信息与计算科学：这一专业融合了数学、计算机科学和信息技术，重点培养学生在数值计算、算法设计和数据分析等方面的能力，是计算机科学与数学结合的典型代表。

统计学：作为现代社会数据分析的核心学科，统计学专业主要聚焦数据收集、分析与推断，部分院校还与大数据技术紧密结合，培养学生在数据分析和处理方面的核心能力。

另外，还有一些交叉学科专业如：

金融数学：这个专业结合了数学和金融学理论，主要培养量化分析和风险管理人才，学生将学习金融市场建模、量化交易等高端技能。

数据科学与大数据技术：整合数学、统计学与计算机科学，目的是在培养具有大数据处理和分析能力的高素质人才，是当前社会中非常受欢迎的高端专业之一。

数理基础科学：一些顶尖院校开设了这一专业，注重数学与物理学的交叉融合，培养具有深厚理论基础和科研能力的高端人才。部分院校还采用数学类大类招生模式，学生入学后可以根据兴趣与专业方向进行分流选择。

二、课程安排

数学类专业的课程体系通常包括基础课程、专业核心课程和实践环节。

基础课程：数学与物理是大多数数学专业的基础，学生将学习数学分析、高等代数、概率论与数理统计、常微分方程等课程。此外，物理学和计算机基础（如C++/Python编程）也常常是基础课程的一部分，帮助学生建立跨学科的思维方式。

专业核心课程：根据不同的专业方向，课程设置也有所不同。例如，数学与应用数学专业会涉及到实变函数、复变函数、泛函分析、微分几何、拓扑学等高级数学课程；而信息与计算科学则包括数值分析、运筹学、数学建模、数据结构、算法设计等课程，旨在培养学生的计算和建模能力。金融数学则重点讲授金融工程、风险管理等课程；数据科学与大数据技术则涵盖机器学习、数据挖掘等前沿技术。

实践环节：数学专业的实践环节同样至关重要。通过数学建模竞赛、科研项目实训和毕业设计，学生能够将所学的理论知识应用到实际问题中。此外，许多院校与金融、IT企业开展了校企合作，提供实习机会，帮助学生更好地融入社会，提升应用能力。

三、就业前景

数学专业毕业生的就业领域极为广泛。无论是传统的科研领域，还是新兴的金融科技和信息技术行业，数学类专业的毕业生都拥有强大的竞争力。

教育与科研：数学专业的毕业生可以选择成为中小学数学教师（需教师资格证），或进入高校和科研院所从事数学理论研究和应用科研。国内顶尖院校，如清华大学、北京大学等，也为数学专业毕业生提供了丰富的科研机会。

金融与经济：随着金融行业对数据分析的需求不断增加，许多数学专业毕业生进入银行、证券、保险等金融领域，成为数据分析师、风险评估师、精算师等。金融科技公司也为数学类专业毕业生提供了丰富的职位，如量化交易、金融建模等岗位。

信息技术：数学专业在信息技术行业中同样大有作为。人工智能、机器学习、数据分析等领域，都需要大量的算法工程师、数据分析师等人才。许多IT企业为数学专业的毕业生提供了丰厚的就业机会。

跨领域发展：除了传统领域，数学专业毕业生还可以选择进入工程计算（如航空航天、能源领域）、生物统计（如医疗数据分析）等行业。此外，政府部门也需要大量数学专业人才为经济规划和统计决策提供支持。

深造路径：对于有志于深造的数学专业毕业生，国内考研和出国留学都是不错的选择。热门方向包括数学、统计学、计算机科学、金融工程等领域，数学专业为考研和留学提供了坚实的学术基础。

总结

全国高校数学科学学院以培养具备“厚基础、强应用”能力的数学人才为目标。课程设置注重理论深度与实践广度的结合，使得毕业生在教育科研、金融科技、信息技术等领域均具有显著的竞争力。随着大数据和人工智能技术的飞速发展，数学类专业的就业前景将继续看好，尤其是在金融、AI等高薪行业，部分岗位的起薪可达15万元以上。因此，选择数学专业无疑是迈向未来科技与经济高端领域的一条理性且具有前瞻性的道路。

在高考志愿填报这个关键的决策时刻，如何让考生最大化录取概率，同时选择合适的专业和院校，成为每个家庭和学子的焦虑焦点。近年来，随着科技的不断进步，AI技术为这一难题提供了前所未有的解答。通过结合IMA（智能个人工具台）和《全国高考指南》，我们可以制定出一个科学高效的志愿填报流程，让每一位考生都能够在信息海洋中精准定位，确保自己的选择既理性又前瞻。

说明：本文仅仅是为了讲解使用方法和案例，对于知识库和 AI 生成内容的真实性不做保证，使用前请用户自行判断。

一、智能化工具，精准分析分数与位置

IMA知识库的核心功能，是通过数据支持和智能匹配，为考生提供个性化的志愿推荐。通过整合近三年的高校录取数据，IMA可以根据考生的分数、位次、选科组合等条件，生成一份“冲、稳、保”院校清单。具体来说，考生只需输入自己的成绩和基本信息，IMA知识库就能快速分析出与之匹配的院校，并预测每个志愿的录取概率（高、中、低风险）。

例如：

假设某考生的分数为600分，位次为全省8000名，选科为物理+化学。IMA知识库会将该考生的情况与过往数据进行比对，生成如下推荐：

冲刺层：985/211院校（如西南大学数学类），录取概率为30%-50%。

稳妥层：重点一本院校（如贵州大学计算机科学与技术），录取概率为60%-80%。

保底层：省属一本院校（如贵州师范大学数学与应用数学），录取概率超过90%。

这一流程让考生能够清晰地看到自己的位置，避免了盲目报考和无意义的“冲刺”，为整个志愿填报提供了坚实的数字依据。

 

二、结合《全国高考指南》进行深入验证

IMA为考生提供了智能化的院校推荐，但高考志愿填报并非仅仅依赖于分数与位次的匹配。为了进一步确认院校和专业的选择是否合理，考生可以借助**《全国高考指南》**这一工具进行深度验证。

《全国高考指南》提供了对各省志愿填报规则的详细解析，列举了每所高校的优势学科、师资力量、硕博点数量、转专业政策等关键信息。通过查阅该指南，考生可以获得更加详细的院校背景资料，确认自己的选择不仅在分数范围内，同时也符合自己的专业兴趣和未来发展规划。

例如：

如果IMA推荐了“杭州电子科技大学”作为稳妥志愿，考生可以进一步查阅《指南》了解该校的计算机学科评估B+，且该校计算机专业被评为“国家级特色专业”，就业率高达97%，起薪约为8k+。通过这些信息，考生可以有信心将其列为自己的“稳妥志愿”，确保填报的决策更为理性与精准。

三、规避风险，避开高风险院校和政策限制

除了分数和专业选择，志愿填报过程中还要特别注意政策限制和潜在的高风险因素。IMA和《全国高考指南》可以帮助考生规避因政策不符而导致的志愿填报失误。

例如：

如果考生想报考“中山大学临床医学（5年制）”专业，IMA知识库可能会提示该校的录取概率为25%（因为考生位次稍低）。而《指南》进一步揭示了该专业的入学要求——必须选择化学+生物科目，并且色弱考生无法报考。通过这种双重验证，考生可以迅速调整志愿，将目标院校调整为“南方医科大学”，它符合自己的学科要求且位次匹配度更高。

四、智能梯度填报，动态优化志愿结构

高考志愿的填报并非简单地选择一两个院校，而是一个复杂的梯度优化过程。结合IMA知识库的智能匹配和《全国高考指南》中的院校数据，考生可以构建一个科学的志愿表结构，涵盖“冲、稳、保”三个层级。

例如：

在浙江省，考生可以根据自己选择的院校数量与专业要求，分配志愿表：

冲刺层：15个志愿，选择浙江大学工科试验班（录取概率40%）。

稳妥层：50个志愿，选择南京邮电大学通信工程（录取概率75%）。

保底层：15个志愿，选择浙江科技学院机械设计制造（录取概率95%）。

通过IMA知识库的实时数据和《全国高考指南》的详细说明，考生能够在志愿填报时灵活调整，不仅填报自己的理想院校，也确保“保底志愿”能稳妥保障自己的录取机会。

类型	数量	示例院校及专业	IMA概率
冲刺	15个	浙江大学工科试验班	40%
稳妥	50个	南京邮电大学通信工程	75%
保底	15个	浙江科技学院机械设计制造	95%

贵州600分理科考生的填写志愿方法：

五、关键注意事项：确保填报无误

尽管AI知识库能够提供精准的分析和推荐，但考生在填报志愿时仍需注意一些细节。IMA知识库的数据更新每年都会同步最新招生计划，而《全国高考指南》需要购买当年的版本来确保信息的准确性。在填报过程中，考生也要特别关注政策红线，如提前批的军校政审要求或师范生的签约限制，避免因忽略细节导致不必要的风险。

最后，避免滑档也是志愿填报中至关重要的一环，考生应确保保底志愿中包含一所本省省属高校，确保能够顺利进入大学。

总结

借助 IMA 知识库的智能匹配与《全国高考指南》的深度数据分析，考生不仅可以迅速锁定志愿目标，还能在填报过程中规避风险，精准选择最适合自己的院校与专业。通过这两者的结合，考生能够最大化录取概率，确保自己的高考志愿填报既理性又科学，稳稳把握未来的学业和职业发展机会。

引言

强化学习作为机器学习的一个重要分支，近十年来在人工智能领域取得了令人瞩目的进展，尤其是在如AlphaGo这样的世界级挑战中，强化学习展现出了强大的决策能力。AlphaGo通过深度强化学习的方法成功击败世界围棋冠军李世石，标志着人工智能在复杂决策问题上的突破性进展。AlphaGo利用深度神经网络与蒙特卡洛树搜索相结合，在每一次棋局中进行模拟，通过强化学习不断调整策略，从而实现了令人震惊的棋局表现。科学家们通过对AlphaGo背后的强化学习算法的分析，揭示了强化学习在复杂决策问题中的应用潜力。

同样，游戏AI（例如星际争霸这款游戏）也大量采用强化学习方法来优化决策、增强智能体的自我学习能力。随着深度学习技术的迅猛发展，强化学习与深度学习的结合逐渐成为解决复杂任务的核心方法之一。而近几个月特别火的DeepSeek等项目更是结合了强化学习与深度学习，推动了AI在复杂任务中的应用。DeepSeek等项目展示了深度强化学习在实际应用中的巨大潜力。通过将深度神经网络引入强化学习，DeepSeek等AI系统能够在极其复杂的环境中进行有效的决策优化，尤其是在大规模数据处理和高维空间的任务中，强化学习结合深度学习的方式能够提供更加准确和高效的解决方案。

在这些前沿的技术背景下，赵世钰研究员的《强化学习的数学原理》为我们提供了一本详细、深入理解强化学习背后数学原理的优秀著作。

本书从强化学习的基础概念讲起，逐步深入到了状态值、贝尔曼方程、值迭代与策略迭代等重要算法的推导，以及蒙特卡洛方法和策略梯度方法的应用。每一章都通过清晰的内容结构图和详细的数学推导，帮助读者理解复杂的算法原理，特别是适合那些希望进一步掌握强化学习深层次内容的读者。而要阅读这本书，读者需要掌握高等代数、线性代数、概率论与数理统计方面的知识，在此基础上来理解这本书会觉得更加容易一些。

详细来看，强化学习作为机器学习的一个重要分支，它的核心思想源于“试错”与“奖励反馈”，即智能体通过与环境的交互不断调整策略，以获得更大的长期回报。这本书从强化学习的基本概念出发，逐步深入探讨了包括状态值、贝尔曼方程、值迭代与策略迭代、蒙特卡洛方法、策略梯度方法等多个重要的数学工具和理论。在书中，每一章都给出了清晰的结构图，帮助读者系统地理解这些复杂的数学原理。下面，我们将对本书的结构进行深入分析，以便更好地理解本书是如何在书中构建强化学习的知识体系的。

本书的最大亮点之一是其深入浅出的教学方式，结合了扎实的理论基础和大量的实践应用。在赵世钰研究员的讲解下，复杂的数学推导得以通俗易懂地呈现，使得即便是对强化学习没有太多背景的读者，也能逐步掌握其核心思想和算法实现。本书通过精心设计的每一章内容，循序渐进地引导读者从理论到实践，从简单的状态值函数到深奥的策略梯度方法，都能在明确的框架中清晰呈现，避免了复杂内容对读者理解的阻碍。每一章的开头都有明确的目标和概述，帮助读者迅速抓住本章的核心内容；而章节的结束又通过总结和思考题，进一步巩固和加深读者的理解。

1. 基本概念与强化学习框架

在第一章，本书详细介绍了强化学习的基本框架，包括智能体（Agent）、环境（Environment）、状态（State）、动作（Action）、奖励（Reward）等核心概念。强化学习的核心思想是智能体通过与环境的交互，依据奖励信号调整自己的行为策略，从而最大化长期回报。这一部分不仅仅是对强化学习理论的概述，更通过具体的数学推导和实例分析，展示了这些概念如何在实际问题中发挥作用，尤其是如何通过优化策略来应对不确定性与复杂性。

2. 状态值与贝尔曼方程

接下来，书中深入讲解了状态值函数的定义及其在强化学习中的作用。本书通过贝尔曼方程的形式来描述状态值与动作值之间的递归关系，为强化学习中的动态规划方法提供了数学基础。贝尔曼方程在强化学习中起到了至关重要的作用，它能够帮助我们从全局最优的角度将问题分解为子问题，从而简化求解过程。在这一部分，本书给出了详细的推导过程，帮助读者深入理解贝尔曼方程的本质及其实际应用。

3. 值迭代与策略迭代

在书的第三部分，本书讲解了值迭代与策略迭代两种经典的强化学习算法。值迭代通过反复迭代更新状态值函数，最终收敛到最优策略；而策略迭代则通过交替更新策略和状态值函数来逐步逼近最优解。本书清晰地展示了这两种方法的数学细节，并且用直观的图示和示例帮助读者理解这两种算法的工作原理。通过这一部分的学习，读者能够掌握如何通过动态规划方法求解强化学习中的最优策略。

4. 蒙特卡洛方法

蒙特卡洛方法作为一种基于随机采样的强化学习算法，书中也给予了充分的讨论。本书详细介绍了蒙特卡洛方法如何通过模拟随机实验来估计状态值和动作值，并通过大量的经验数据来逼近最优策略。这种方法不依赖于环境模型，尤其适用于那些无法显式建模的复杂环境。通过图文并茂的描述，本书清晰地阐释了蒙特卡洛方法的基本原理及其应用，帮助读者在实践中有效利用这一方法。

5. 策略梯度方法

在书的最后，本书深入讲解了策略梯度方法，这是一种基于梯度上升的强化学习算法，用于直接优化策略的参数。策略梯度方法在深度强化学习中有着广泛应用，尤其是在高维度的复杂任务中，策略梯度方法可以避免传统值迭代方法在大规模状态空间中的计算瓶颈。本书通过清晰的推导与实例，帮助读者理解如何利用梯度上升算法优化强化学习模型，从而提高决策性能。

书籍结构与阅读体验

《强化学习的数学原理》全书结构清晰，内容层次分明，每一章都以理论推导为基础，并辅以丰富的图示，帮助读者逐步消化和理解抽象的数学概念。书中不仅对强化学习的基本原理进行了详细讲解，还涵盖了现代强化学习中的一些高级技术，如策略梯度方法和深度强化学习的结合。本书通过生动的案例分析，尤其是结合如AlphaGo、游戏AI等实际应用，帮助读者更好地理解这些数学原理在真实世界中的应用场景。

《强化学习的数学原理》是一本内容丰富、结构严谨的专业书籍，适合那些希望深入了解强化学习背后数学机制的读者。不仅适合作为大学生或研究生的教材，也非常适合工程师或研究人员用来作为提高自己强化学习理论水平的参考书。无论是从基础的状态值函数、贝尔曼方程到复杂的蒙特卡洛方法、策略梯度方法，本书都做了细致的讲解，确保读者能够掌握强化学习的核心概念和方法。另外，书中大量图示和实例的应用，也使得这些数学原理更加易于理解，尤其对于强化学习初学者来说，具有重要的启发意义。通过本书，读者不仅能掌握强化学习的基础理论，还能了解其在现代人工智能领域中的前沿应用，特别是如何通过强化学习与深度学习的结合，推动智能决策系统的发展。

1. 充分使用文档、日历和会议功能

企业级通讯工具（钉钉、飞书、企业微信等）都具备协作功能，它们不仅仅是沟通工具，更是信息整理和时间管理的重要助力。在会议之前，建议提前创建相关文档，并要求团队成员提前阅读。这种开会之前先整理文档、阅读加评论的模式，不仅能够让每个参与者都事先了解会议的内容和目标，还能大大提升会议效率。通过提前准备，会议中可以集中讨论关键问题，而非浪费时间在信息共享上。每次会议结束之后需要输出会议纪要，并分配行动项。这样可以确保会议的每个决策都能够落实，并且不留信息死角。每次会议前后都进行有效的时间管理和总结，避免了反复讨论、重复工作的情况。

很多职场人士都遇到过外出开会的情况，尤其是需要参加几十公里以外的现场会议时，往往会浪费大量时间在路程上。为了避免这种情况，建议在可能的情况下，尽量选择线上会议来代替现场会议。通过视频会议工具，可以节省往返的时间，更高效地进行信息交换和决策讨论。特别是在繁忙的工作日，减少现场会议的时间开销，可以让职场人士更专注于实际的工作内容，避免被无意义的出差或长途会议打断工作节奏。

除此之外，实时聊天工具中集成的日历功能可以帮助职场人士有效地安排工作时间和会议时间。避免过多的临时拉会以及会议间的过多插播，最大限度减少无效会议对工作时间的影响。通过将所有重要事项都在日历中记录下来，你可以清晰地看到自己的时间被如何分配和消耗。

更重要的事情是，日历不仅仅用于安排会议，职场人士也可以记录自己每天的工作任务和所耗费的时间，甚至是在工作中时间浪费的地方。例如，当你发现某个任务花费的时间远远超出预期时，可以通过回顾日历来分析原因，进一步优化工作流程和安排。需要注意的是，这份日历记录的数据只供自己查看和优化，并不需要对同事或领导公开。这是一种自我管理的工具，帮助你提高工作效率，并识别可能的时间浪费，在未来的工作中进行效率的提升。例如，回顾过去的一周或者一个月，哪些项目或任务花费了过多时间，哪些沟通方式可以更高效，哪些会议可以合并或避免。这些都是优化自己时间管理的机会，能够帮助我们在未来的工作中更加高效地安排时间。

高效的时间管理不仅依赖于工具和方法，更重要的是通过时间的积累与习惯的培养，使得时间管理变成一种“自动化”过程。每个职场人士都可以通过逐步培养一些良好的工作习惯，帮助自己管理好每天的工作和时间。例如，养成每天开始工作前列清单的习惯，每天结束时回顾当天工作进展的习惯，这些简单的习惯可以大大提高工作的效率和清晰度。设定固定的工作时间和休息时间也是时间管理的一部分。在工作时间内，专注于工作任务，而在休息时间尽量远离工作，给自己充分的休息与恢复。通过养成这些规律的工作习惯，职场人士能够更好地掌控工作节奏，避免工作过度与时间浪费。

2. 提前安排工作，避免临时任务干扰

在职场中，临时任务往往是时间管理的大敌。许多人一到公司，就面对一堆需要立即处理的Excel文件、PPT资料或其他紧急事务。虽然这些任务看似小且紧急，但它们会迅速占据你的工作时间，打乱原定的工作计划。为了避免这种情况，建议在每天开始工作之前，先花几分钟对当天的工作进行规划。提前安排好工作内容，并优先处理最重要和最紧急的事项。这样可以避免临时任务的干扰，确保自己在工作中有足够的时间进行深度思考和高质量的输出。

现代职场中的人常常面对多任务并行的情况，许多人自认为能够同时处理多个任务，这种多任务处理的方式可能会导致效率的下降。但是，当我们试图同时处理多个任务时，大脑需要不断切换注意力，这样不仅降低了专注力，还容易出错。最有效的时间管理方法是“单任务处理法”，即一次集中精力处理一个任务，直到完成后再进入下一个任务。通过专注于一个任务，职场人士可以更好地保持注意力，提高工作质量，同时减少因任务切换带来的时间浪费。在实践中，设定一个“专注时间段”也是一种不错的方式。可以设定一定的时间（比如25分钟），全身心投入工作，避免中途查看手机或与他人交谈，保持高效。

3. 合理安排开发进度：保持工作的持续性

在软件开发等技术岗位上，进度安排尤为关键。没有合理的进度安排，开发工作可能出现一阵忙一阵闲、或者脉冲式的工作局面，造成资源浪费和工作压力波动。因此，合理规划开发进度是职场人士管理时间的一项重要任务。制定阶段性的工作目标，并在每个阶段结束时进行评估，既能保持工作持续性，又能避免开发过程中由于缺乏规划而产生的焦虑和压力。通过持续跟进和调整计划，可以确保工作的流畅性和任务的有序完成。

在职场中，任务往往是多种多样的，而且时间紧迫。在这种情况下，如何合理安排任务的优先级，成为了有效管理时间的关键。一个常见的工具是“爱森豪威尔矩阵”，它将任务分为四类：紧急且重要、重要但不紧急、紧急但不重要、不紧急也不重要。在日常工作中，首先应集中精力处理紧急且重要的任务，这些任务往往关系到工作进度和结果的直接影响。其次，处理重要但不紧急的任务，这些任务对于职业发展和长期目标至关重要，但却常常被忽视。通过这种优先级管理，职场人士可以在纷繁复杂的工作中保持清晰的头脑，避免被琐碎任务分散精力。

结语：合理规划，成就高效职场

在现代职场中，时间就是生产力，如何管理好自己的时间，已经成为每个职场人士成功的关键。通过合理提前安排工作任务、巧妙运用会议和日历功能，避免过度多任务处理、定期回顾与反思，我们可以更好地管理自己的工作时间，减少不必要的时间浪费。与此同时，我们可以培养良好的时间管理习惯，学会拒绝不必要的任务，让自己在繁忙的职场中保持高效，最终成就一个更充实、更有成效的职业生涯。时间不等人，只有有效地管理时间，才能在职场中游刃有余，迎接更多的挑战与机遇。

对于每一个打工人而言，目标感在职场中的重要性不可忽视，它不仅是打工人动力的源泉，更能激发打工人源源不断的创造力。对于企业而言，重视并提升员工的目标感，针对不同的员工设计不同的目标，让员工从工作本身找到热爱与归属，将企业的目标和员工的目标尽量地放在同一条轨道上。只有当员工对自己的工作充满热情，感知到个人目标与企业愿景的紧密契合，他们才会全身心投入其中，持续创新并不断突破自我。目标感激发了员工的主动性和创造力，促进了工作效率的提升，并加强了对企业的忠诚度，这对于任何希望长期发展并维持竞争力的组织来说，都是至关重要的。

在当今快速发展的职场中，企业需要的已不仅仅是完成任务的工人，而是能够创造价值、推动创新的创造型人才。创造型工作强调的是员工的思维能力、问题解决能力和创新意识，而不仅仅是简单的重复劳动。企业应当通过提供能够激发员工创造力的工作内容和环境，吸引那些有志于实现自我价值的优秀人才。通过这样的方式，企业不仅能够招募到技术娴熟的执行者，更能吸引到具有独立思考和创新精神的战略性人才，这些人才将推动公司持续发展并在长期竞争中脱颖而出。

对于企业而言，吸引并留住优秀人才是每个企业都面临的挑战。为了做到这一点，除了在招聘的时候，尽可能地争取各种各样的优秀人才之外，在日常的管理中企业的管理者也需要按照既定的目标分解任务，并以员工对工作内容本身的热爱为核心出发点，尽可能地给员工安排其喜欢的工作内容。同时，管理者可以通过定期与员工交流，帮助他们发现或唤醒内在的目标感，从而提升他们的工作积极性和忠诚度。以下是管理者可以询问员工的五个关键问题，它们能够帮助员工找回对工作的热情，激发他们的潜能。

1. 你擅长做什么工作？

作为管理者，第一步是帮助员工认识到自己的强项，尤其是应届生和刚入职公司没多久的员工。管理者可以通过提问：“你擅长做什么工作？”“在同样的工作量下，哪些工作你花费的精力较少？”可以帮助员工时刻进行自我审视，并在日常繁重的工作中找到自己的优势所在。这两个问题不仅能够让员工思考自身的核心能力，还能帮助他们意识到自己在团队中的独特价值，从而激发他们更积极地发挥这些优势。

2. 你喜欢做什么工作？

每个人都希望做自己热爱的工作，毕竟兴趣是最好的老师。管理者可以通过询问员工：“你喜欢做什么工作？”“在正常的工作日，你最期待做哪些任务？”来帮助员工发现他们的工作激情。在企业中，工作不应该仅仅是任务的堆砌，它还应当是员工内心充满动力和喜悦的源泉。当员工能够做自己喜欢的工作时，他们不仅能提高效率，还会感受到工作带来的满足感。

3. 什么类型的工作让你感到最有价值？

对于每个员工来说，虽然大部分人工作的目的是为了生计，但我想更高的层次是为了实现个人价值和职业目标。管理者还可以问员工：“在过去的一段时间里，哪些工作成果让你感到最为自豪？”“你完成了哪些对团队或组织至关重要的任务？”管理者可以帮助员工识别他们的工作对组织的重要性，甚至可以把更重要的工作安排给合适的员工。这些问题能够让员工看到他们工作的内在价值，并激发他们为更高目标而努力的动力。

4. 是什么给了你前进的动力？

每个人在工作中都有一个驱动力，管理者可以通过“你学到了哪些将来会用到的技能？”“你今天所做的工作是否让你更接近自己的愿望？”等问题，帮助员工发现自己的前进方向。工作不仅是为了眼前的任务，它还是员工通往未来目标的桥梁。通过明确自己的目标，员工将更加清晰地看到自己努力的方向和动力来源，从而更有动力去追求更高的成就。

5. 你如何与同事相处？

团队协作是现代职场中不可或缺的一部分。管理者可以通过提问：“你与哪些同事关系最适合？”“如果整个办公室的同事都是你喜欢的人，场景会是怎样的？”来帮助员工思考如何与同事建立更好的人际关系。工作中良好的合作氛围不仅能增强团队的凝聚力，还能让员工感到他们在工作中找到了归属感，从而增强工作的意义感。

结语

通过这五个简单而深刻的问题，管理者能够帮助员工更清晰地认识自己、发现自己的热情，进而激发他们的内在目标感。当员工能够在工作中找到自己的价值与意义时，他们不仅能为企业创造更大的价值，也能够在职业生涯中获得更多的满足与成就。为了吸引和留住优秀人才，重新设计工作本身，让员工找到对工作的热爱，将是成功的关键所在。

在职场上，有的时候会出现一种奇怪的现象，正在悄无声息地消耗着人的价值。

在招聘的时候，岗位的职责和内容明明写的是“算法工程师”，但是在候选人入职之后却要背负起后端开发、前端搭建、数据分析、测试开发，甚至是各种边边角角的杂活。对于一名算法工程师而言，不仅要做会议记录，要做服务器维护，连日常的excel数据报表也得一个个出，还有想象不到的各种各样项目对接、繁重的流程和技术文档撰写、流程混乱的跨部门沟通，这些已经统统被塞进算法工程师的日常待办里。最讽刺的是，当这些杂乱无章的任务终于在一片疲惫中堆叠完成时，管理者却开始反问算法工程师：“你怎么在算法上没有成果？怎么AI项目还没有突破？还不能够让AI做到减少人力和减轻负担的效果？”

在这种岗位上，一个典型的算法工程师，明明是在专攻机器学习、深度学习这些复杂课题的技术人才，结果突然变身为项目经理，跨部门沟通小能手，后端开发大神，前端布局专家，甚至还得做数据清洗、做测试开发，和测试人员一起深夜守在业务旁边死磕。唯一的共同点是——每个任务都没有时间给你真正专注做。于是，身为一位“全能”的技术人才，他被要求同时兼顾这些不同领域的工作，连各种各样的日报、周报、双周报、月报、季度报、半年报和年报都得自己来。反而最需要投入深度的算法研究，被推到了“闲暇时间”的角落，长期等着“有空再做”的状态。

对于某些公司而言，算法的突破，仿佛是在碎片化劳动、疲于奔命中，凭空诞生的奇迹。仿佛一个工程师，只要加班熬夜、不断堆工时，就能自动产出深度学习模型，就能轻松攻克科研课题。仿佛一个工程师，只需要在睡梦中做梦，就能够在梦中实现AI的算法开发，达成意想不到的算法效果。

AI算法开发是需要一定的创新能力的，可真正需要产出创新的岗位，需要的是什么？是深度的思考，是高密度的专注，是反复试错和沉淀，而不是在每天数十个小任务中疲于奔命，不是把注意力分成无数碎片，不是在无休止的救火和打杂中消磨殆尽。简单来说就是给得太少：这里给得太少并不是指工资给得很少，而是管理者不给时间，不给专注的空间，不给明确的边界感。同时，管理者又对算法工程师要得太多：要你全能，要你无所不能，要你在一片杂乱中还能天才地爆发，在服务器都少之又少的前提下还希望有巨大的产出。这本质上，不是对个人的挑战，而是对职业角色的深度误解。

如果管理者希望算法工程师承担起整个产品的研发工作，那不如直接把“全能型人才”的名字印在招聘广告上，标明“招聘全能型工程师”，这样或许更合适——这样的候选人他不仅需要做算法，还得做产品设计，做架构开发，做项目经理，做前后端开发，做数据分析，做项目管理，成为PPT和EXCEL工程师，甚至还要为公司的整体战略和布局负责。

到最后让人不解的是，虽然管理者已经把很多额外的职责都压给他，最终却仍然对他没有任何宽容，反而把对AI成果的期望推得越来越高——“做出AI突破”、“产出创新”，“行业领先”、甚至希望“超越竞争对手”。这一切，似乎都没有考虑到他的时间和精力早已被无限分配。在忙碌完各种需求之后，AI终于有了一定的产出，但是更加让人无奈的是，管理者却又说“AI只是锦上添花，项目交付才是雪中送炭”。真正让人气愤的是，往往这样的要求背后，管理层只会关注短期内的“完成情况”，而忽略了创新和技术突破背后需要长时间的专注和积累。却不见他们提出过“给你更多的资源”、“让你专注做技术”的方案。创新需要土壤，而不是不间断的碎片时间和加班文化。

在工作中，每个角色的价值，都是需要被尊重的。让算法工程师做后端、前端、测试、运维，是对专业的稀释；让创意型工作在碎片中挣扎，是对产出的扼杀。当一个岗位需要承担四五个岗位的职责时，其实早已失去了基本的职业尊重。当一个组织习惯于压榨式使用人才时，它正在透支的不仅是人的体力，更是创新力、责任感和未来的可持续发展力。短期看，似乎解决了燃眉之急；但长期看，最宝贵的人才，只会在沉默和疲惫中，悄悄流失。或许对于某些公司而言，招聘的目的并不是提升自身的技术实力，而是在海量招聘中筛选到某些合适的人并长期留用，其他不合适的人只需要及时离开就可以了。

真正成熟的组织，懂得给角色留空间，让专业的人做专业的事，不要让各种各样的杂事拉打扰专业的人。管理者需要懂得设定合理预期，让创新建立在专注、探索和持续打磨之上，而不是建立在无尽打杂之中。想要算法上的突破，就要在管理上先突破短视；想要技术上的飞跃，就要在制度上先尊重专注。别再让“给的很少，要的很多”成为职场的常态。别再让真正有创造力的人，在无意义的疲惫里，变成一颗颗沉默的螺丝钉。

一个合格的企业应该懂得角色的专业性和深度，懂得为创新提供足够的时间和空间，而不是一味要求员工成为“全能神”。真正有眼光的领导，应该知道，技术和创新需要一颗宁静的心，需要日复一日的专注，而不是在千头万绪的琐事中迷失自我。别再让这种“给得很少，要的很多”的荒谬逻辑，成了职场中唯一的标准。让每个岗位都能专注于自己的本职工作，才能创造出真正的价值，才是每个企业应追求的目标。