在极远极远的过去，数学界的世界一片璀璨，几座神奇的城池横亘在这片土地上。首先是“算数丘城”，那里住着微分方王、积分方伯、变换方公和几何王子。他们的城池，虽然有时风景如画，却总是布满了各种极限、收敛与发散的迷雾。然后是“群体之城”，它有一个独特的结构，既有哈密顿广场、概率城、又有李群大道；每一条路都被不等式区隔开来，深藏着许多离散与连续的深奥谜题。

在这些城池间，有一条河流叫做“代数溪”，河水清澈见底，充满了各种群的原型，有时流得急促，有时又变得缓慢。每年都有不计其数的流派聚集在这条河边，讨论群的性质、环的结构、域的扩展与代数方程的解法。这里的村民过着不平凡的生活，他们的名字或许听上去十分熟悉，却隐藏着无穷的数学智慧。村头有一个老教授，名叫“高斯”，他以开拓尺规作图正十七边形、无穷大和无穷小的疆域而闻名。人们常听到他传授在“复数村”创造的奇迹，讲述那些关于欧拉公式和复变函数的故事。他的居所是一座古老的塔楼，塔楼上刻着不朽的名句：“真理总是深藏在解的边缘”。高斯的朋友，黎曼，也常常出现在塔楼里，二人就黎曼猜想、黎曼曲面、以及曲率问题热烈争辩。每当他们辩论激烈，塔楼外的风会变得狂乱，仿佛在回荡着无数未解的数学疑问。

再往北行，便是“概率城”，在这座城市里住着伯努利兄弟、拉普拉斯和伯努利兄弟。这里有一条名为“标准正态分布河”的河流，水流宽广，急速湍流。每天清晨，贝叶斯与费马都会围绕着先验概率与后验概率进行激烈的争辩，哪怕只是为了讨论一小块概率密度的形状。这个城市的特色之一是人们常穿着拉普拉斯设计的“概率服”，那种衣服不仅能让人隐形，还能隐藏所有的不确定性。还有柯尔莫哥洛夫（Kolmogorov）这位数学家，将概率论进行公理化，让大家都围绕着这个体系运作。

在“算数丘城”与“概率城”的交界处，坐落着一座神秘的“映射宫殿”。这座宫殿的结构极为复杂，每一层都通过不同的映射连接。映射宫殿的主人是一个著名的数学家，他的名字叫做“康托尔”（Cantor）。他以研究“集合论”和“无穷”而著名，在他的宫殿中，所有的物体、事件和空间都可以通过不同的映射被彼此联系。每一扇门、每一根柱子、甚至每一根绳索，都与“康托尔集”上的点有着某种微妙的对应关系。宫殿的屋顶是无穷的分形图案，时刻在变化，时而显现出细致的维数，时而展现出无限的自相似。

在康托尔的宫殿深处，有一个大大的“基尔伯特空间”，这是一个神秘的地方，拥有着极高的数学价值。基尔伯特空间里没有传统意义上的点，只有数不清的“向量”和“超函数”。这里的每一件物品都是一个函数，每一条线段都是一个向量，甚至连空气中的气流也是由无穷多个谱系的正交基所组成。在这里，赫尔曼·闵可夫斯基（Minkowski）和特奥多尔·冯·纽曼（Von Neumann）正在密切合作，他们探索着量子力学与数学结构的奥秘，甚至深入到数学与物理的交汇点，讨论着如何通过线性代数与算子理论来描述量子态的变换。

映射宫殿的周围有一片神秘的“拉普拉斯湖”，湖水清澈见底，但却流动着无尽的概率波动。每当月光照耀在湖面上时，波动的几率与函数就会以极其奇异的方式交织成美丽的图案，仿佛是某种奇异的统计分布。湖边常有一位老者坐在岩石上冥思，他就是“马尔科夫”（Markov）。他身着“随机过程长袍”，时而低声自语，时而向前方的极限倾诉。马尔科夫的最大贡献是“马尔科夫链”理论，这也是他在随机过程领域的独到之处。人们经常听到他谈论“平稳过程”、“独立增量”，以及如何运用“马尔科夫不等式”预测未来的随机事件。

在“几何山谷”，几何大师欧几里得、阿基米德、高斯的几何派弟子、黎曼和罗巴切夫斯基的弟子聚集在一起，讨论着平面几何与空间几何的奇妙图形。这个地方藏着一座几何宝塔，塔上有一行古老的铭文：“所有直线都汇聚在无穷远处。”这座塔的周围有一个神秘的区域，叫做“李群园”，园内的树木都是由群论构成，每一棵树都有一个独特的群表示，群木的枝繁叶茂像极了复杂的群结构。

在“微积分之海”，牛顿和莱布尼茨常常一同乘船，遨游在无穷小的浪花之间。他们的讨论内容永远不离求导与积分的美妙，有时他们也会偶尔停下来，向他们的同伴，欧拉、达朗贝尔与拉格朗日展示他们为数不多的数学成果。微积分的每一个波动都充满了创造与启发，仿佛数的精灵在海面上自由舞动。

继续往南，穿越“积分荒原”，你会遇到一座座如同“黎曼几何”的“石塔”，这些石塔中藏着一位又一位著名的数学家。这里有“菲尔兹”塔、还有“赫尔德”塔，它们的顶端都镶嵌着用“拉普拉斯变换”雕刻的精美图案，标志着这些伟大数学家的无穷探索和成就。而塔下，总有学者在进行“拉格朗日乘数法”和“柯西-施瓦茨不等式”的比试，看谁能在复杂的条件下，找到最优的极值。

再往东，远远的“拓扑村”伫立在群山之中。在这里，庞加莱总是与拉克莱布和斯图尔特一同，探讨拓扑空间与同调理论，探讨扭结、缠绕、孔洞与映射之间的千丝万缕的关系。这里的树是由不连续的空间组成，根部在无限小的空间中能看到“李群”的影子。每当这些拓扑学者散步时，脚下的道路会变形、拉伸，仿佛在展现那些神秘的同伦群。在“拓扑村”的深处，有一个叫做“类比道”的地方，专门用来讨论“同伦”和“同调”的问题。这里的居民是一些专门研究“拓扑空间”的学者，他们常常在村庄里讨论“连通性”、“紧性”以及“欧拉示性数”。每年的秋天，这里会举行一场盛大的“同调竞赛”，数学家们需要借助“霍普夫映射”和“阿特伍德定理”将不同的拓扑结构归约到一个标准化的模型。赛场上，选手们展示了他们的“拓扑不变量”，各种“嵌入定理”与“同调群”在空中飞舞，仿佛能触碰到天空的极限。

而在“微分方程之峡谷”中，常常传来阵阵高亢的讨论声。这里的住民是一群钟情于微分方程的学者，最著名的当属“欧拉-拉格朗日”二人组。欧拉总是在研究如何用“常微分方程”来刻画物理现象，而拉格朗日则致力于通过“变分法”来发现最优解。在这片峡谷中，人们有时还会见到一位“卡尔曼”大师，他带着一只神奇的“卡尔曼滤波器”，总能在复杂的动态系统中，提取出最重要的“状态估计”。每当卡尔曼大师走进峡谷，附近的树木、河流、甚至空气中的噪声都会开始静默，仿佛都在等待着他对“最优控制理论”的深刻解答。

在“度量空间山脉”的另一端，有一片“概率森林”。这片森林有着独特的规律，任何一棵树的生长都遵循“泊松过程”，森林的土壤中充满了“不确定性”，每一片叶子都是一个随机变量。森林的深处藏着“贝叶斯-帕松-拉普拉斯”三位贤者，他们经常在这里探讨如何通过“贝叶斯网络”来建构统计模型，或者如何通过“极大似然估计”来预测未来的事件。

在“矢量空间平原”上，众多数学家们像欧几里得、阿基米德、笛卡尔等，都在这片广袤的平原上留下了他们的足迹。在这片广阔的领域内，“线性代数”的大师总是带着他的“矩阵”与“特征值”，在不断地将不同维度的空间互相转换，创造着极限与无限之间的美丽画卷。除此之外，还有一片广袤的“希尔伯特平原”，平原上生长着众多的数学森林和神秘的定理山脉。其中有一条通往“范畴之城”的道路，这条路是由“范畴论”铺设的，它用一条“同构”桥连接着不同的数学领域。这个城市的建设者是“埃尔朗”（Eilenberg）和“马尔基厄尔”（Mac Lane），他们共同创造了“范畴论”的基础，强调了数学结构间的关系与变换。每当人们走进范畴之城，都会看到“函子桥”和“自然变换塔”巍然矗立，仿佛在讲述一个个不同领域之间的“同伦”与“同调”的深刻联系。

在城市的北部，有一片被称为“模糊逻辑草原”的广袤区域。这里住着“扎德”（Zadeh），他是“模糊集合”理论的奠基人。这片草原的特殊之处在于，任何物体的边界都变得模糊不清，定义变得不再是明确的零和一。在这里，“模糊集合”和“隶属度函数”像是草原上飘动的风，能够让不确定性和模糊性在数学中得到应用。

再往东，进入了一个被称为“数值分析岛”的地方，岛上遍布着“高斯-赛德尔迭代法”和“雅可比法”的魔法阵。岛屿的中心有一座神秘的“数值逼近塔”，塔内住着和“库塔”（Martin Kutta），他们经常在塔内探讨“数值解法”和“误差分析”。塔顶悬挂着一块“收敛性”铭文，表明只有那些能在有限步骤内求得近似解的算法，才配得上进入塔顶。

岛屿的西面，有一座高耸的“图论山”，山顶处矗立着欧拉（Euller）和其他数学家，他们共同建立了图论的经典理论，推动了“图的着色”和“图的遍历”这两项基础理论的诞生。这里的居民时常以“图的连通性”与“欧拉回路”讨论，时而利用“斯图尔特定理”来指导他们如何在复杂网络中找到最佳路径。在岛屿的南方，是一片充满数理逻辑和不确定性的“哥德尔沼泽”，这个地方的主人是“哥德尔”（Gödel），他以其“不可判定性”定理著称。哥德尔沼泽中的水面时常漂浮着一些“自指”与“递归”的奇怪生物，它们不停地在“数理模型”中穿梭，试图破译“形式系统”的奥秘。这里的空气充满了“逻辑推理”的味道，每当春风吹过时，就会出现一阵“哥德尔不完全性”的阵阵回响。

南方不远，有一座叫做“拓扑荒野”的地方，荒野中住着斯坦因（Steenrod）与塞尔（Serre）。他们探索了拓扑学的边界，在此建立了“同调理论”和“层理论”。拓扑荒野的地形总是令人迷惑，时而平坦如“霍普夫环面”，时而曲折如“克莱因瓶”。这里的每一块岩石、每一棵树、每一滴水都充满了“连续性”和“同胚”的特性，仿佛能在无限的变换中保持不变。

而在“统计王国”的深处，住着“费舍尔”（Fisher）、“诺伊曼”（Neumann）与“皮尔逊”（Pearson）三位巨匠，他们共同开创了“统计推断”的新时代。在这里，密布的“概率密度森林”和“回归分析草原”里，弥漫着“不确定性”的气息。居民们时常在“极大似然估计”与“最小二乘法”的指引下，走向真理的彼岸。每当“费舍尔方差分析”传出声音时，周围的“抽样”与“假设检验”便会随着算法的变化而起伏。

在这片充满智慧和奥秘的“数学大地”上，有一座神秘的“计算机科学宫殿”。这座宫殿的建设者是“图灵”（Turing），他不仅是“图灵机”理论的创始人，还揭示了计算和可计算性的极限。宫殿的中心是一个巨大的“图灵测试”大厅，里面时常有来自各个领域的数学家和工程师在测试人工智能的极限，进行着一场场关于“算法复杂性”和“计算模型”的深刻对话。

计算机科学宫殿的周围有一片“信息论森林”，在这片森林中，“香农”（Shannon）和“哈夫曼”（Huffman）时常聚集在一起，讨论信息的“压缩”与“编码”问题。每当他们挥动手中的“信息熵公式”时，森林中的鸟儿似乎也开始发出更具“信息量”的鸣叫，仿佛在向世界传递着知识的真谛。

在“数学帝国”的东南角，有一片被称为“动力系统之海”的地方，那里充满了涌动的波涛与湍流。这里的领主是“庞加莱”（Poincaré），他是混沌理论的奠基人之一。在这片海洋中，任何一个小小的扰动都会引发系统的剧变，仿佛在传达着“初始条件敏感性”的深刻道理。海面上漂浮着“李雅普诺夫指数”的符号，预示着“稳定性”与“不稳定性”之间的永恒博弈。沙滩上存放着“斯梅尔马蹄”，象征着稳定的系统也会带来混沌。

在复数的世界里中，存在着两位伟大的数学探险家——Fatou与Julia。他们穿越了复数平面的神秘荒原，创造了复动力系统的基石。他们通过不懈的研究，发现了在复平面上，某些函数的迭代过程会演化出令人惊异的图形。Fatou专注于研究这些迭代过程的稳定性，而Julia则深入探索了这些过程的边界行为。他们的工作奠定了复动力学的基础，揭示了复数上“吸引域”和“逃逸域”之间复杂而美丽的关系。尽管他们的发现曾一度被忽视，但他们留下的理论为后来者铺设了通往深奥几何的道路。五十年后，一位名叫Mandelbrot的数学家，他仰望着复数平面的星空，发现了更加神秘的景象。他用无穷迭代的技术，揭示了一个无穷小的区域，这个区域的边界既不规则又精美，像是自相似的图案重复展开。这就是分形的起源，Mandelbrot集——一个既简单又极为复杂的图形，它的边界充满了无穷的细节。每次放大，它都展现出崭新的世界，如同数学世界的无尽宇宙，充满着无尽的可能性与奇迹。与此同时，Dennis Sullivan站在前人发现的基础上，揭开了一个新的谜题。他用极其精细的拓扑手段，证明了一个深刻的命题——有理函数没有游荡区间。他向世人展示了复数上的拓扑结构的力量，证明了无论多么复杂的函数，在适当的条件下都必须遵循某种精确的秩序。Sullivan的工作为动力系统带来了新的光辉，揭示了在混沌的世界中，依然隐藏着无法逃脱的内在秩序。

这些地方和人物共同构成了21世纪前的数学风景画，承载着数不尽的定理、公式与想法，像一条条交织的河流，永远流向未知的远方。此时此刻，四方的数学巨匠与神秘的数学力量共同演绎着世界的奇妙构造，无论是微分方程的华丽舞步，还是拓扑空间的神秘网格，亦或是代数群的无穷回响，都在这片土地上勾画出数学无穷尽的美丽与奥秘。

备注：

1. 高斯 (Gauss) – 德国数学家，贡献包括数论、概率论、复变函数等。

2. 黎曼 (Riemann) – 德国数学家，以研究复变函数和几何方面的贡献著称，尤其是黎曼猜想。

3. 伯努利兄弟 (Bernoulli) – 瑞士数学家家族，主要贡献在概率论和流体力学等领域。

4. 拉普拉斯 (Laplace) – 法国数学家、天文学家，贡献包括天体力学、概率论。

5. 欧几里得 (Euclid) – 古希腊数学家，被誉为几何学的奠基人。

6. 庞加莱 (Poincaré) – 法国数学家、物理学家，拓扑学的奠基人之一。

7. 牛顿 (Newton) – 英国数学家、物理学家，微积分的创始人之一。

8. 莱布尼茨 (Leibniz) – 德国哲学家、数学家，微积分的共同发明者之一。

9. 康托尔 (Cantor) – 德国数学家，集合论的创始人之一，提出了不同大小的无穷集合。

10. 马尔科夫 (Markov) – 数学家，特别是马尔科夫过程的研究者，马尔科夫链理论的重要人物。

11. 卡尔曼 (Kalman) – 美国数学家，卡尔曼滤波器的发明者，广泛应用于控制理论与信号处理。

12. 黎曼几何 (Riemannian Geometry) – 由黎曼创立的一种几何学，研究曲面和流形的性质。

13. 柯西-施瓦茨不等式 (Cauchy-Schwarz Inequality) – 数学中著名的不等式，涉及向量的内积空间。

14. 范畴论 (Category Theory) – 由埃尔朗和马尔基厄尔发展，强调对象和态射之间的关系。

15. 模糊集合 (Fuzzy Set) – 扎德提出的集合理论，允许元素具有模糊的隶属度。

16. 高斯-赛德尔迭代法 (Gauss-Seidel Iteration) – 数值分析中的迭代方法。

17. 图论 (Graph Theory) – 研究图形结构的数学分支。

18. 哥德尔不完全性 (Gödel Incompleteness) – 哥德尔提出的定理，表明任何足够强大的数学系统都存在不可判定的命题。

19. 极大似然估计 (Maximum Likelihood Estimation) – 一种估计参数的方法，常用于统计推断。

20. 图灵机 (Turing Machine) – 图灵提出的计算模型，是理论计算机科学的基础。

当初在国外读博时，我的代数教授对范畴论（category theory）情有独钟，甚至亲自写了两本书，一本是关于环论的，另一本则深入探讨范畴论。每当代数考试临近时，他总爱出一些涉及群论、环论、模论和范畴论的题目，而域论和伽罗华理论却鲜有涉及。虽然教授的书籍颇具深度，但其中的内容往往艰涩难懂，且并不完全契合我的学习口味。于是，无奈之下，我只好前往图书馆翻阅其他参考书，经过一番查找，我偶然发现了 Serge Lang 的《代数学》。然而，翻阅之后，我意识到这本书虽然丰富，但并不完全符合教授考试的风格，最终它只能作为额外的学习补充材料。

终于，在图书馆翻阅了一番后，我找到了这本书——《Algebra: Chapter 0》。这本书不仅涉及范畴论，但却没有那么晦涩难懂，且充满了丰富的例子，极大地激发了我的兴趣。它由Paolo Aluffi编写，是一本研究生水平的代数教材，属于美国数学学会（AMS）《Graduate Studies in Mathematics》系列的第104卷。全书分为九章，内容从集合论和范畴论的基础知识开始，逐步深入群论、环与模、线性代数、域论以及同调代数等核心领域。

书中的第一章“预备知识”通过朴素的集合论和范畴论介绍基本概念，并强调普遍性质（universal properties）在代数中的重要性，为后续章节的学习奠定了坚实的理论基础。第二至第四章系统地探讨了群的结构，包括群同态、自由群、商群和群作用等内容，同时结合Sylow定理与对称群等经典例子，深化了对群论的理解。第五至第七章则聚焦于环论和模论，内容涵盖了唯一分解整环、多项式环的因式分解以及线性代数中的自由模理论。最后，第八章和第九章转向同调代数，研究张量积、Ext和Tor函子等高级工具，并最终以导出范畴和谱序列作为总结。

这本书，正是应对考试所需的必备教材！

个人感觉，本书特别适合具备一定数学成熟度的读者，尤其是那些已接触过基础抽象代数但希望以更现代的观点重新审视该领域的学者，也适合研究生。其范畴论框架不仅统一了分散的代数概念，还为后续学习代数几何、表示论等提供了语言准备。此外，书中包含大量非传统例题（如由整除关系定义的范畴），挑战读者对代数结构的常规认知。该书以范畴论的语言为框架，系统介绍了抽象代数的基础概念和高级主题，为读者提供现代数学的统一视角。

1. 范畴论视角：不同于传统教材，Aluffi从范畴论的角度重构代数概念，如将商集、直积等构造描述为特定范畴中的初始或终对象，凸显数学结构的普适性。例如，集合的并和积分别对应范畴中的余积和积，而群同态的基本定理则通过范畴的泛性质自然呈现。
2. 强调普遍性质：书中反复出现“universal property”这一主题，将其作为理解代数对象（如自由群、张量积）的核心工具。例如，自由群的构造通过遗忘函子的左伴随定义，而多项式环的泛性质则刻画了其在交换环范畴中的唯一性。
3. 渐进式难度设计：前四章适合本科学生，涵盖标准群论和环论内容；后五章逐步引入高阶主题，如诺特模、Jordan标准形及Galois理论，适合研究生阶段学习。每章末尾的习题既巩固基础知识，又延伸至模形式、四元数等拓展内容。
4. 历史与动机结合：在引入新概念时，作者常辅以历史背景或直观动机。例如，同调代数的章节始于拓扑中的链复形类比，帮助读者理解代数与几何的联系。

在国外读博的第一个假期里，我几乎把自己泡在了图书馆，每天背着那本书来回穿梭于图书馆和住处之间。当图书馆还没开门时，我便坐在门口的长桌旁，开始埋头学习。整个假期，我几乎是这样度过的，熬过了无数个日日夜夜。终于，在第二个学期开始时，我顺利地通过了代数的博士资格考试，一次性解锁了这一关。那一刻，我长舒了一口气，心头的重担终于卸下，代数的世界也仿佛远离了我——如同所谓的“forget algebra”。

生平简介

Gaston Maurice Julia（1893年2月3日－1978年3月19日）出生于法属阿尔及利亚的Sidi Bel Abbes。他自幼展现出对数学和音乐的浓厚兴趣，后进入巴黎高等师范学院（École Normale Supérieure）和巴黎大学深造。第一次世界大战期间，21岁的Julia应征入伍，并在战斗中遭受重伤，失去了鼻子，此后终生佩戴皮革面罩遮盖伤处。战后他重返学术生涯，成为法国数学界的核心人物，晚年于巴黎逝世。

数学贡献

Julia集与分形理论

Julia最著名的贡献是提出了Julia集的概念。1918年，25岁的 Julia 发表了199页的里程碑论文《有理函数迭代备忘录》（Mémoire sur l’itération des fonctions rationnelles），系统研究了复平面上有理函数的迭代行为，奠定了全纯动力系统理论的基础。这一成果为他赢得了法国科学院大奖（Grand Prix des Sciences Mathématiques）。 尽管他的工作一度被遗忘，直到20世纪70年代，Benoit Mandelbrot在研究分形时重新发掘并推广了Julia的理论，使Julia集与Mandelbrot集成为分形几何的核心内容。

学术影响与遗产

Gaston Julia 与 Pierre Fatou 共同开创了复动力系统的现代理论。他的研究涉及复分析、几何学、量子理论数学基础等领域，出版30部著作，如《Eléments de géométrie infinitésimale》（1927）和《Cours de Cinématique》（1928），他还培养了Claude Chevalley等著名数学家。《Oeuvres》（6卷，1968–1970）收录其全部研究成果，《Traité de Théorie de Fonctions》（1953）是函数论经典教材。

个人生活与家族

Julia的儿子Marc Julia是著名有机化学家，发明了“Julia烯烃化反应”。尽管身体残疾，Julia始终活跃于学术前沿，其坚韧与才华使他成为20世纪数学史上的标志性人物。

荣誉与纪念

二战后他继续任教于巴黎大学和巴黎综合理工学院，1934年当选法国科学院院士，1950年任院长。 1970年代，Mandelbrot 通过计算机可视化复兴了Julia的工作，使其理论在分形几何中重获关注。Julia 的成就通过分形理论的普及被广泛认可，其名字永久关联于数学中美丽的 Julia 集图形。他的多部著作被收录于《数学科学史百科全书》，而 MacTutor 数学史档案等资源持续记录他的学术遗产。

20 世纪最具影响力的数学家之一

斯蒂芬·斯梅尔（Stephen Smale，1930年7月15日－）是20世纪最具影响力的数学家之一，以其在拓扑学、动力系统、经济学和计算理论等领域的开创性工作而闻名。他出生于美国密歇根州弗林特市的一个工程师家庭，从小展现出对数学的兴趣，但高中时期的学业表现并不突出。1948年，他进入密歇根大学学习物理，随后转向数学，并于1957年在拉乌尔·博特（Raoul Bott）的指导下获得博士学位，研究方向为微分拓扑。

斯梅尔的数学生涯充满了突破性贡献。1961年，他证明了五维及更高维度的庞加莱猜想（Poincaré Conjecture），这一成果震惊了数学界，并为他赢得了1966年的菲尔兹奖。他的证明方法引入了一系列拓扑方法和“h-配边定理”（h-cobordism theorem），这些工具成为微分拓扑领域的核心。他在动力系统领域的研究也极具影响力，特别是他构造的“马蹄映射”（Smale horseshoe），为混沌理论奠定了基础，并广泛应用于非线性动力学、气象学和生物数学等领域。

但是斯梅尔的学术生涯并非一帆风顺，他于1948年进入密歇根大学学习之后，他是一名不错的学生，被选入由鲍勃·索尔（Bob Thrall）教授的荣誉微积分课程，并取得了优异的A成绩。然而，在大学二年级和三年级期间，他的成绩平平，大多是B和C，甚至在核物理这门课上得了F。斯梅尔于1952年获得了理学学士学位。尽管成绩不佳，但凭借一些运气，他仍被密歇根大学数学系录取为研究生。然而，在研究生阶段的前几年，他的表现依然不佳，平均成绩仅为C。当系主任希尔德布兰特（Hildebrandt）威胁要将他开除时，他才开始更加认真地对待学业。最终，斯梅尔于1957年在拉乌尔·博特（Raoul Bott）的指导下获得博士学位，并开始在芝加哥大学担任讲师，由此开启了他的学术生涯。

在里约的沙滩上寻找马蹄映射

斯蒂芬·斯梅尔在1960年春天前往巴西里约热内卢的访问，成为他数学生涯中一段极具传奇色彩的经历。当时他获得了美国国家科学基金会（NSF）的资助，选择前往里约热内卢的纯粹与应用数学研究所（IMPA）进行学术交流。这段时期不仅孕育了他最重要的数学突破，也留下了”在里约海滩上完成伟大证明”的佳话。在里约工作期间，斯梅尔保持着独特的研究习惯，他常常带着笔记本来到著名的科帕卡巴纳海滩，在沙滩上思考数学问题。这种非传统的工作方式后来引发了一些争议，但也成为他创造性思维的象征。正是在这样的环境中，他同时完成了两项里程碑式的成果：动力系统中马蹄映射的发现和高维庞加莱猜想的证明。

马蹄映射（Smale horseshoe）的发现是斯梅尔在里约期间最重要的贡献之一，这一发现彻底改变了人们对动力系统的理解。当时斯梅尔正在研究结构稳定性问题，受到同事Mauricio Peixoto的启发，他开始深入思考动力系统的长期行为。在里约海滩上的思考中，他构造出一个简单而深刻的几何模型——马蹄映射，这个模型展示了一个确定性系统如何产生看似随机的行为。马蹄映射的核心思想是通过拉伸、折叠的几何变换，展现出动力系统中对初始条件的敏感依赖性，这后来成为混沌理论的基石之一。这一发现不仅为混沌现象提供了严格的数学描述，也为后来的动力系统研究开辟了全新方向。

在拓扑学领域，斯梅尔在里约期间完成了对高维庞加莱猜想的突破性证明。庞加莱猜想是拓扑学中最著名的未解决问题之一，其核心是探讨如何通过局部性质判断一个空间是否等同于球面。斯梅尔采用创新的微分拓扑方法，成功证明了该猜想在五维及更高维度上的正确性。他的证明引入了革命性的”斯梅尔手术”技术，通过系统地处理流形上的奇异点，最终建立了h-配边定理。这个定理不仅解决了庞加莱猜想的高维情形，还为流形的分类提供了强有力的工具。值得一提的是，斯梅尔在里约的证明过程极具个人特色，他常常在研究所和海滩之间往返，将深奥的拓扑思考与里约的自然环境奇妙地融合在一起。

而斯梅尔的数学觉醒始于他对庞加莱（Henri Poincaré）”同宿点”（homoclinic point）理论的重新发现。在里约热内卢数学研究所（IMPA）的图书馆里，斯梅尔偶然翻阅了美国数学家伯克霍夫（George Birkhoff）的著作集，其中详细记录了庞加莱在研究三体问题时提出的同宿点概念。庞加莱曾发现，在保守系统中，稳定流形和不稳定流形的横截相交会产生极其复杂的动力学行为，他将这种现象称为”同宿纠缠”。这一发现曾让庞加莱本人都感到震惊，以至于他在《天体力学新方法》中写道：”这一现象的复杂性令我震撼，我甚至不愿尝试描绘它的图景。”然而，这一深刻见解在随后的几十年里几乎被数学界遗忘，直到斯梅尔通过伯克霍夫的著作重新发现了它。

与此同时，斯梅尔正与动力系统领域的另一位关键人物——麻省理工学院的诺曼·莱文森（Norman Levinson）保持着密切的学术交流。莱文森在1949年对英国数学家卡特赖特（Cartwright）和利特尔伍德（Littlewood）关于非线性振动的研究进行了严格化，他们的工作揭示了某些微分方程中存在的复杂解行为。莱文森在给斯梅尔的信中指出了他早期猜想中的一个错误，这个批评成为斯梅尔思想转变的催化剂。斯梅尔后来回忆道：”莱文森的信像一道闪电，击碎了我原有的认知框架，迫使我重新思考动力系统的本质。”在里约海滩的反复推演中，斯梅尔将莱文森描述的复杂行为与庞加莱的同宿点理论联系起来，逐渐形成了”马蹄映射”的雏形。

前苏联数学家庞特里亚金（Lev Pontryagin）和安德罗诺夫（Alexander Andronov）的结构稳定性理论构成了影响斯梅尔的第三个重要思想来源。通过他在普林斯顿高等研究院的同事所罗门·莱夫谢茨（Solomon Lefschetz），斯梅尔接触到了苏联学派关于”粗糙系统”（即结构稳定系统）的研究。庞特里亚金和安德罗诺夫在1937年提出，许多物理系统可以用在微小扰动下保持定性性质的动力系统来描述。斯梅尔的巴西同事莫里斯·佩肖托（Mauricio Peixoto）曾跟随莱夫谢茨学习，他将这一理论传统带到了巴西。斯梅尔敏锐地意识到，庞特里亚金的结构稳定性理论与他自己正在思考的问题存在深刻联系，但苏联学派的研究因排除了同宿现象而显得过于局限。

在这三重理论背景的交织下，斯梅尔于1960年初在里约的海滩上完成了他的两大突破。在科帕卡巴纳海滩的某个下午，他忽然领悟到庞加莱的同宿点必然导致马蹄结构的出现。他后来描述这一顿悟时刻：”当我将同宿点的概念与莱文森描述的复杂行为联系起来时，整个图景突然变得清晰起来。”马蹄映射的精妙之处在于，它通过简单的几何操作（拉伸、折叠）展现了确定性系统中的内在随机性：一个二维映射将正方形区域拉伸变窄后折叠成马蹄形，通过迭代这个过程，系统会表现出对初始条件的极端敏感性——这正是混沌的核心特征。斯梅尔证明，这种马蹄结构在出现同宿点的系统中是普遍存在的，从而为混沌现象提供了第一个严格的数学框架。

几乎在同一时期，斯梅尔在拓扑学领域也取得了惊人突破。多年来，他一直被庞加莱猜想所困扰，这个猜想探讨如何通过代数不变量来识别球面。在里约期间，斯梅尔发展出了一套全新的微分拓扑方法。他创造性地将动力系统中的思想引入拓扑学，提出了”斯梅尔手术”技术，通过系统地处理高维流形上的奇异点，最终证明了五维及更高维度的庞加莱猜想。这一证明的关键在于h-配边定理的建立，该定理表明在某些条件下，两个流形之间的配边实际上是一个平凡配边。斯梅尔后来回忆，这一突破同样发生在里约的海滩上：”有一天，当我看着海浪周而复始地拍打沙滩时，突然想到了如何通过逐层消解流形上的奇点来构造同胚。”

斯梅尔在里约的这段科研经历展现了跨学科思想交融的强大创造力。他将庞加莱的天体力学直觉、莱文森的严格分析技巧和庞特里亚金的结构稳定性观点融为一体，最终在动力系统和拓扑学两个领域同时取得重大突破。这种独特的学术轨迹也反映了20世纪中叶数学发展的一个显著特征：不同学派、不同传统的数学思想在全球范围内的流动与碰撞。斯梅尔的工作不仅解决了具体难题，更重要的是建立了连接不同数学分支的新范式，为后续的混沌理论、微分拓扑和动力系统研究开辟了广阔的道路。正如他后来所说：”数学中最美妙的事情往往发生在你让不同领域的想法自由对话的时候。“斯梅尔后来回忆说，里约的海滩为他提供了理想的思考环境，阳光、海浪和轻松的氛围帮助他突破了传统思维的束缚。这种非传统的工作方式虽然一度引起NSF对其研究经费使用的质疑，但最终产出的卓越成果证明了其有效性。斯梅尔的这段经历也成为数学史上的一个传奇，展示了伟大数学发现可能诞生在最意想不到的环境之中。从马蹄映射的发现到庞加莱猜想的证明，斯梅尔在里约的短暂停留永久地改变了多个数学领域的发展轨迹。

斯梅尔马蹄映射

斯梅尔马蹄映射（Smale’s Horseshoe Map）是动力系统理论中的一个经典模型，由数学家Stephen Smale在1960年代提出。它通过简单的几何变换，揭示了混沌动力系统中的复杂行为，如无限周期轨道、非周期轨道以及拓扑熵的存在。马蹄映射的核心在于拉伸、折叠和压缩的操作，使得系统在迭代过程中产生高度复杂的动力学行为。

1. 马蹄映射的几何构造

初始设定

考虑一个矩形区域 （例如单位正方形 ）。马蹄映射 的作用是将这个矩形进行非线性拉伸和折叠，使其在水平方向上拉长，在垂直方向上压缩，并弯曲成“马蹄”形状。

拉伸与折叠

1. 水平拉伸：首先，矩形 DDD 在水平方向上被拉伸（例如，长度变为原来的 倍，）。

2. 垂直压缩：同时，在垂直方向上，矩形被压缩（高度变为原来的 倍，）。

3. 弯曲折叠：拉伸后的长条被弯曲成“U”形或“马蹄”形，并重新放置在原矩形区域上方，使得它横跨原矩形的两个垂直条带（例如，左右各占一部分）。

迭代过程

每次应用映射 ，矩形都会被拉伸、压缩并折叠一次。逆映射 则相当于反向操作，即垂直拉伸、水平压缩，并反向折叠。

2. 马蹄映射的动力学行为

不变集与混沌

在无限次迭代后，某些点永远不会离开矩形 ，这些点的集合称为不变集 。 是一个Cantor集（分形结构），由无限多个离散点组成，具有自相似性。这个不变集上的动力学行为是混沌的，即：存在无限多个周期轨道（任意长度的周期），存在非周期轨道（永不重复的轨道），系统对初始条件敏感依赖（微小变化导致长期行为完全不同）。

符号动力学与混沌

马蹄映射的不变集 可以与符号动力学（Symbolic Dynamics）对应：每个轨道可以用一个二进制序列（如 ）表示，其中“0”和“1”分别代表点在每次迭代中落在左侧或右侧条带。这种对应关系表明，马蹄映射的动力学行为等价于伯努利移位（Bernoulli Shift），即一个无限符号序列的混沌系统。

3. 马蹄映射的意义

Smale 马蹄映射是第一个严格证明的混沌系统之一，它展示了如何从简单的几何变换中产生极其复杂的动力学行为。它解释了横截同宿点（Transverse Homoclinic Points）的存在如何导致混沌（Poincaré曾发现同宿点，但Smale用马蹄映射严格证明了混沌的存在）。它广泛应用于非线性动力系统领域、天体力学、工程与物理中。

4. 直观理解

想象一个橡皮筋被拉伸、压缩并折叠成一个马蹄形，然后再次拉伸、压缩并折叠。每次操作都会使橡皮筋的结构更加复杂，最终形成一个无限精细的网状结构（Cantor集）。在这个结构中，任何微小的扰动都会导致完全不同的未来轨迹，这正是混沌的本质。Smale马蹄映射的美妙之处在于，它用如此简单的几何操作，揭示了自然界中广泛存在的混沌现象。它不仅是一个数学构造，更是理解复杂动力系统的一把钥匙。

斯梅尔的学术生涯

在学术职位上，斯梅尔曾先后任教于哥伦比亚大学（1960–1964）、加州大学伯克利分校（1964–1995）和香港城市大学（1995–2002），并在伯克利分校退休后成为荣誉教授。在2003至2012年期间，斯梅尔担任丰田工业大学芝加哥分校的教授；此外自2009年8月1日起，他开始担任香港城市大学的特聘教授。斯梅尔的研究兴趣广泛，晚年还涉足计算理论和数理经济学。他研究了“牛顿法”在数值计算中的收敛性问题，并提出了“斯梅尔问题”（Smale’s problems），即“P vs. NP”问题的数值版本。在经济学领域，他与经济学家合作，探讨了一般均衡理论和市场动态的数学结构。他的多学科研究展现了他对数学及其应用的深刻理解。

斯梅尔的卓越贡献为他赢得了多项顶级荣誉，包括菲尔兹奖（1966）、美国国家科学奖章（1996）和沃尔夫数学奖（2007）。他的工作不仅解决了高维庞加莱猜想这样的重大难题，还推动了动力系统、计算理论和经济学的发展。许多数学概念以他的名字命名，如斯梅尔马蹄、斯梅尔手术和斯梅尔问题，这些成果至今仍在数学和科学领域产生深远影响。

2002年退休后，斯梅尔仍保持对数学研究的热情。他的职业生涯体现了数学家对社会责任的关注，以及跨学科研究的价值。正如数学家迈克尔·阿蒂亚（Michael Atiyah）所说：“斯梅尔是那种罕见的数学家，他不仅能解决难题，还能改变整个数学的走向。”斯蒂芬·斯梅尔的生平和成就，无疑为现代数学留下了不可磨灭的印记。

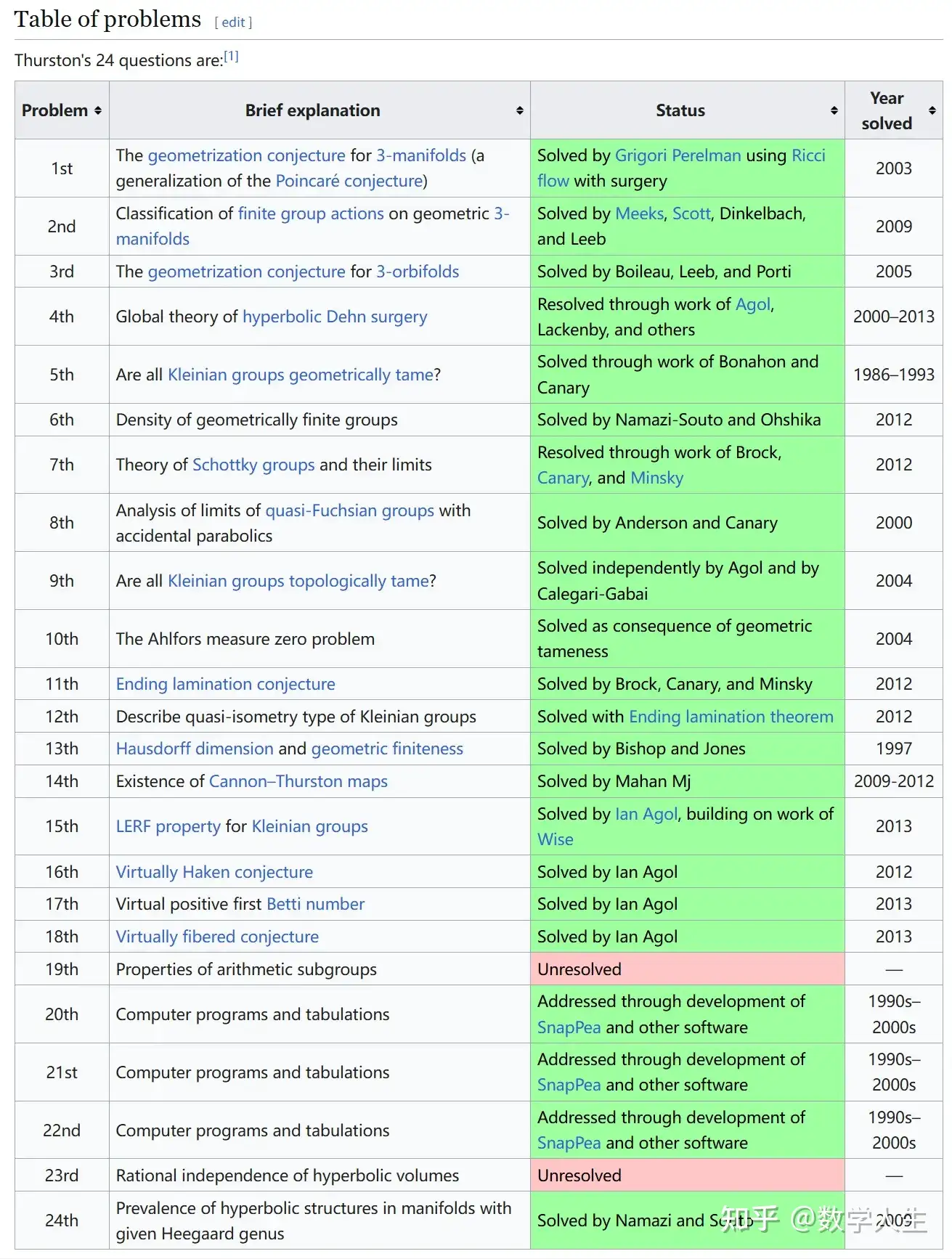
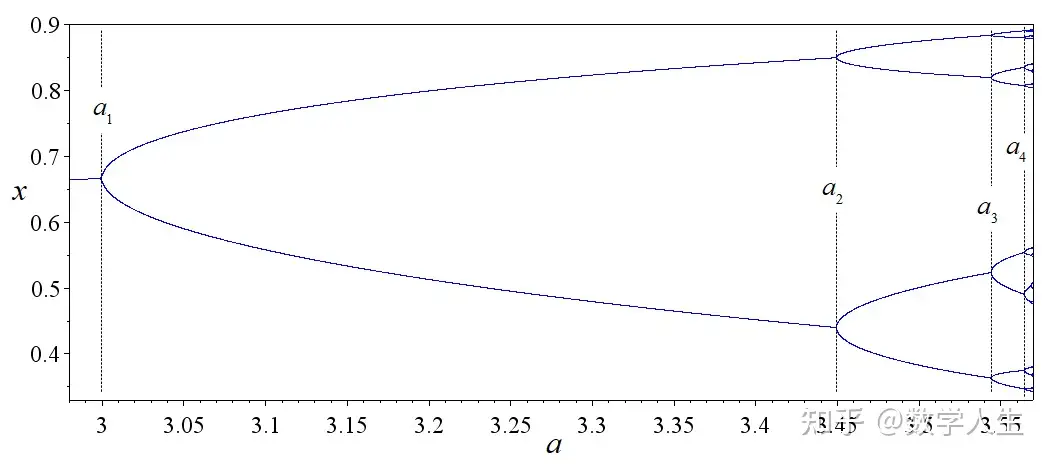
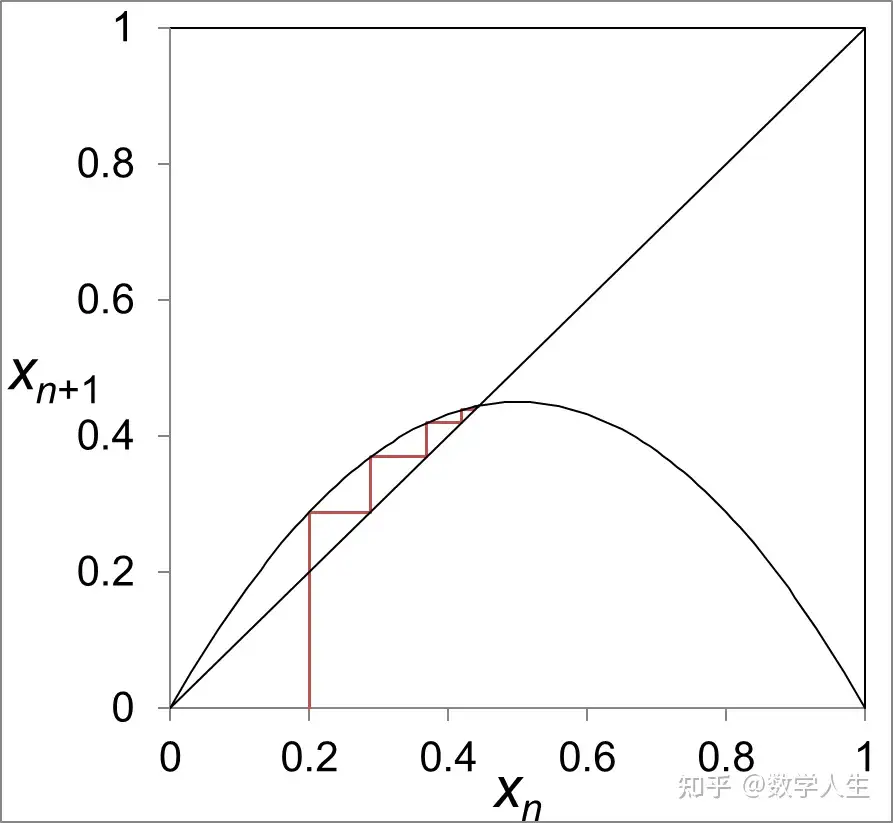
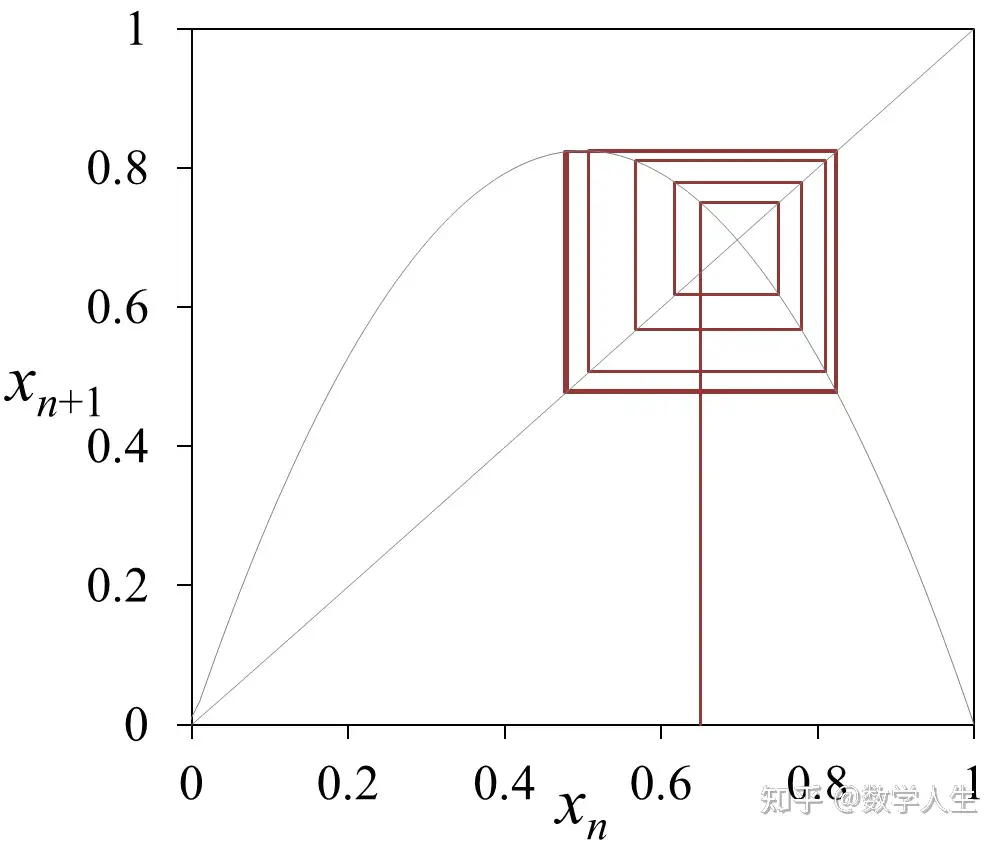
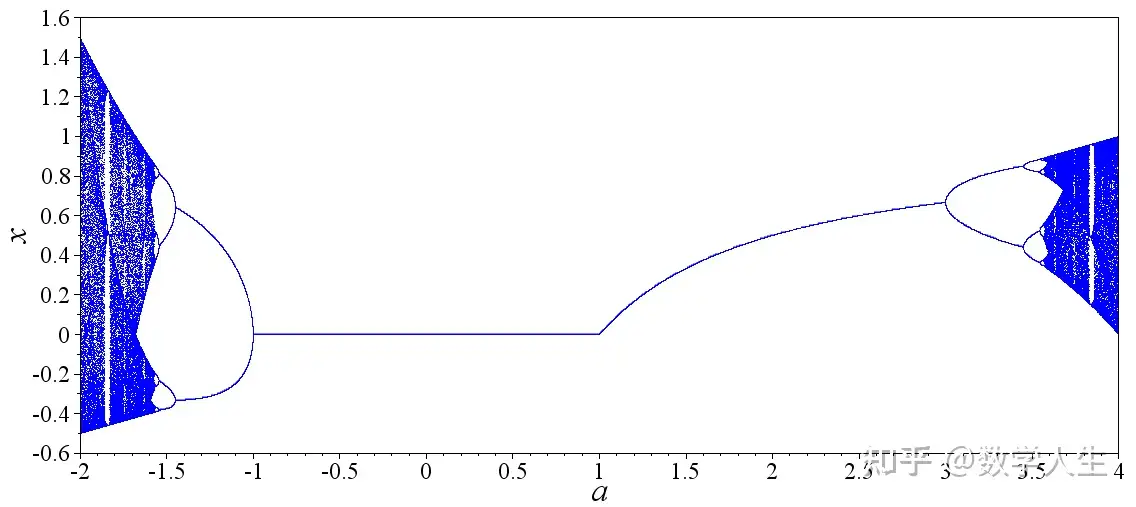
William Thurston（昵称 Bill）是 1982 年数学界最高奖菲尔兹奖得主，2012 年去世。他的数学研究就像进行魔术表演，总是突然就从帽子里抽出绝妙的创意，无数次让世界范围内的数学家们惊叹不已。1970-1980年间，Thurston 的研究工作在拓扑学领域引起了一场翻天覆地的革命，对数学界的影响一直持续到现在。

Dennis Sullivan 是 2010 年数学界另一个大奖沃尔夫奖得主，在代数拓扑和复动力系统两个领域为数学界作出深刻的贡献。Thurston 和 Sullivan 的研究有着很大的交集。当 Sullivan 得知 Thurston 去世的消息后，他迅速写下了这十个记录他们之间来往的故事。

撰文｜Dennis Sullivan

翻译｜杜晓明

故事一

1971 年 12 月，在伯克利召开的一个动力系统研讨班结束的时候，貌似解决了一个能很好地应用于动力系统的平面上的棘手问题。解决方案宣称：能把 N 个两两位置不同的点逐步移动到另外的 N 个点，使得在移动过程中不发生自交，并且每一步都整体只移动非常小的距离。坐在前排的资深动力系统专家们都乐观地相信这个结果，因为根据之前的经验，在三维以及更高维数的动力系统的应用中，由于这些点能摆成一般位置，这个结论显然是对的，如今该定理在二维的情形也应该成立。

一个坐在教室最后排的长头发、大胡子的研究生站了起来，说证明中的算法是不成立的。他就是 Bill Thurston。他怯怯地走到黑板前面，画了两幅图，每幅图都有 7 个点。然后开始按照刚才的算法来操作。一开始出现的连线尽管很短很少，但毕竟挡住了另外一部分线的延伸方向。想把另外一部分线继续延长又同时避免出现交叉的话，必须从别的地方绕回来，于是各条线开始变得越来越长。在这个复杂的图示例子里，刚才的算法无效！我从未见过其他人有如此强的理解力，也从来没见过有人能如此之快就创造性地构造出反例。这让我从此对几何上可能出现的复杂性产生敬畏。

各个时期（上世纪70 年代、80 年代、90 年代）的 Thurston。

故事二

几天之后，伯克利的研究生们邀请我（那时我也同样是大胡子、长头发）在分隔办公区与电梯区的走廊墙壁上画一些与数学有关的壁画。就在准备画的时候，故事一里面提到的那位研究生跑来问我：“你觉得画这个东西有意思吗？”他给我看的是平面上围着三个点绕来绕去的一些复杂的一维对象。我问：“这是什么？”他的答案让我很惊讶：“它是一条简单闭曲线。”我说：“这一定很有趣！”

于是我们就开始花几个小时一起在墙上画这条曲线。这真是一次非常棒的学习如何粘贴的体验。为了让这条曲线看起来较美观，首先得画一些较短的、彼此平行的、有些弯曲的短线（正如叶状结构局部方形邻域内的图案一样），然后再把它们光滑地接起来。我问他是如何想到这样的曲线的，他说：“从一条给定的简单闭曲线出发，不停地沿着中间的相交曲线作成对的 Dehn twist。”

这幅 2 米高、4 米宽、画着曲线的壁画（见2003年《美国数学会通讯》第50卷第3期的封面）署有作者和日期：“DPS and BT, December, 1971”，它在伯克利的墙上保留了40多年，直到几年前才被擦去。

过去在伯克利 Evans Hall 里由 Thurston 和 Sullivan 一起画的壁画。这个围着三个点绕来绕去的复杂图像实际上是一条简单闭曲线。| 摄影：Ken Ribet

故事三

上面两个故事在伯克利发生的那个星期，其实我只是从麻省理工学院访问伯克利，讲一系列关于微分形式和流形同伦论的课。那时候叶状结构与微分形式到处出现，并且成为研究的热潮，我想利用在我的研究中出现的1-形式来描述基本群的中心下降序列，进而构造叶状结构。这些叶状结构的叶子覆盖了从流形到它的幂零流形的映射图像。幂零流形就是从基本群的高阶幂零子群出发构造的流形。这其实是把利用同调来构造的到高维环面的 Abel 映射推广成幂零的情形。由于缺少 Lie 群的知识，我曾向麻省理工学院和哈佛大学的微分几何学家们请教这个推广的可能性，但我自己还是没弄明白。这些都太模糊、太代数化了。

来到伯克利之后，我在第一次课上就提出这方面的问题，并私下里与 Bill 进行讨论。开始我并没有抱什么希望，因为这是奇怪的代数与几何的混合体。然而第二天，Bill 就想到了彻底的解决方法，并且给出了完整的解释。对于他来说，这些只是很初等的东西，涉及的几何知识也不多，仅仅是 Elie Cartan 的 dd=0 的对偶形式中的 Jacobi 关系。

就在以上两个故事发生期间，我向我的老朋友 Moe Hirsch 提起了 Bill Thurston。Thurston 是 Moe 的博士生，那时候正处于博士阶段的第五年。我记得是 Moe 还是谁说过，Bill 开始念博士时进展很缓慢，甚至在口试时出了点小问题。当时 Bill 被要求举一个万有覆盖的例子，他选择了画亏格为2 的曲面的万有覆盖，在黑板上画出一些笨拙的八边形，八个八边形共用一个顶点。

亏格 2 曲面的万有覆盖。

这种论证很快就在黑板上越来越呈现为没有说服力的混乱。我想 Bill 是第一个在考场上想出如此非平凡的万有覆盖的人。Moe 说，不久之后，Bill 便开始以每个月一个的速度解决博士论文级别的大问题。许多年之后，我听说就在那段时间里， Bill 刚好有了他的第一个孩子 Nathaniel。孩子在晚上不睡觉，所以 Bill 也没法睡觉。在念研究生的时候，有一整年的时间，他晚上都只能与 Nathaniel 在地板上来回地走。

在伯克利度过的那一周改变了我的人生。我很感激命运让我有幸欣赏到所谓的“莫扎特现象”，并且认识了一位新的朋友。我刚从伯克利回到麻省理工学院，就马上把这一切告诉我在麻省的同事们。但我想我的热情过于强烈了，以致没法让别人全部理解：“我遇到了自己所见过的、甚至从没期望会遇到的最好的一位研究生。”

我安排 Bill 先去普林斯顿高等研究院（IAS），然后来麻省理工学院做一场报告，并计划把他招到麻省理工学院。但最后的结果是，Bill 在 1973-1974 年来麻省理工学院访问了一年，但那一年我正好去访问法国高等科学研究院（IHES），并且在法国一待就是 20 年。而 Bill 则被邀请回到普林斯顿大学任职。

故事四

普林斯顿高等研究院，1972-1973

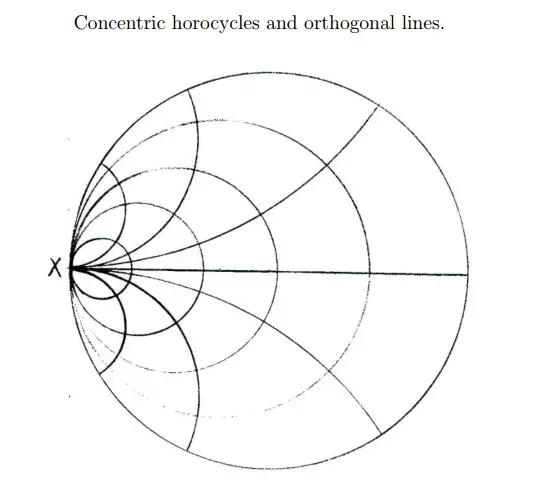
在 1972-1973 这段时间，我从麻省理工学院访问普林斯顿，于是与 Bill 接触的机会更多了。一天，我们从普林斯顿高等研究院出来准备去吃午饭。我问 Bill，什么是极限圆（horocycle）。他说：“你们待在这儿别动。”然后他开始向学院的草地走去。走了一段距离，他停住并转过身来，说：“你们在以我为圆心的圆周上。”然后他转身走得更远，再次转过身来说了一些东西。由于距离远，他说什么我已经听不清楚了。他每走到一个新的地方就再喊一次，我们终于知道他说的是同样的意思：“你们在以我为圆心的圆周上。”接下来他走得更远了。由于距离太远，他喊什么我都听不见了。等他转过身来使劲喊大概同样意思的时候，我忽然知道了什么是极限圆。

极限圆

Atiyah 问我们其中某些拓扑学家：平坦向量丛是否存在分类空间？他曾对这样的丛构造出一些新的示性类。由 Brown 定理，我们知道这东西存在，但是还不知道如何具体地构造出来。第二天，Atiyah 说，当他问 Thurston 这个问题的时候，Thurston 给出了一个神奇的构造：把作为向量丛结构群的李群看成一个抽象群，赋予离散拓扑，然后就给出分类空间。

后来，我听说 Thurston 通过画图证明给 Jack Milnor 看：任意单峰映射的动力系统模式都会出现在取适当值c时对应的二次函数 x → x2+c 的迭代中。我因为正在学习动力系统，所以就计划花一个学期的时间在普林斯顿，向 Bill 学习这篇从刚才提到的画图而发展出来的关于 Milnor-Thurston 万有性的著名论文。

故事五

普林斯顿大学，1976 年秋

1976 年 9 月，我准备去普林斯顿大学学习一维动力系统，而 Thurston 则已经发展出曲面映射的新理论。我刚到的时候，他在高等研究院做了三个小时精彩的即兴演讲来解释这个理论。我非常幸运：因为有之前在伯克利的墙上画那条曲线的艰苦劳动，由此启发，Thurston 关于叶状结构的极限的主要定理直观上对我来说非常清晰。在我待的那个学期即将结束的时候，Thurston 告诉我，他相信这些东西对应的映射环面具有双曲度量。我问他为什么，他说不知道如何向我解释，因为我没有充分理解微分几何。

在我离开普林斯顿之后的几个星期里，Bill 没有我的干扰，有更多时间从事研究。对于特定的 Haken 流形，他完成了双曲度量存在性的证明。而对于映射环面的情形，他后来又花了两年多的时间。其中的细节本文后面会说。

在 Bill 讲授的一门一学期课程里，研究生和我都学到了很多关键的思想：

• “双曲几何在无穷远处变成共形几何”的类比。让人印象深刻的是，Bill 处理的方式是在双曲空间内部而不是在无穷远边界处，他关注的是一个特殊的模型。这给我带来完全不同的心理体验。
• 我们学会极限点凸包的边界曲面的内蕴几何。一天，Bill 来上课，他在讲台上转动一个他自己做的精巧的纸制装置，不停地旋转，而他却不说任何话，直到我们领悟出平坦性为止。
• 我们还学到了双曲曲面的厚薄分解。我记得 Bill 在普通房间的黑板上画出有 50 米长不停环绕的曲面薄块。忽然一切明朗起来，包括如何解释在几何上收敛到 Riemann 曲面组成的模空间上著名的 Deligne-Mumford 紧化上的点。

后来 Sullivan 在课上讲解带很“薄”的部分的双曲曲面。

1976 秋，我在普林斯顿整整待了一个学期。Bill 和我讨论如何理解 Poincare 猜想，希望证明一个对所有三维闭流形都成立的更一般性的猜想。我们的想法是建立在三维是相对较低的维数这个基础之上。我们在一篇小文中论述，只要能证明三维闭流形都有共形平坦坐标，就可以证明整个 Poincare 猜想。我们决定在这个问题上共同花上一年。然而，当时在那儿学习的一位名叫 Bill Goldman 的本科生在几年之后证明了这个前提是不正确的。（如果上数学家家谱网站查师承关系，可以查到 Thurston 与 Goldman 都是Hirsch 直接指导的博士。Thurston 为 Hirsch 带来的学术后裔有 200 多个，而 Goldman 则带来 30 多个。除了他们俩之外，Hirsch 的其他博士带来的学术后裔加起来没几个。）

接下来，Bill 在普林斯顿发展了 quasi-Fuchsian 型 Klein 群的极限的理论，来寻找映射环面上的双曲结构。与此同时，我在巴黎努力想解决 Ahlfors 的极限集零测度猜想。一年之后，他的研究取得了关键进展（把尖点封闭上了），而我的研究则在否定的方向上取得了极大进展（证明所有与已知 Klein 群信息有关的遍历论方法都是不够的，有太多深层次的非线性障碍）。在一次瑞士阿尔卑斯山上召开的会议上，我们对比了各自的笔记。他的整个映射环面证明计划虽然完成了，但是证明过程非常复杂。而我否定方向的信息则能把 Mostow 刚性定理推广成一般性的结论，这能在相当大的程度上简化 Bill 在纤维化情形下的证明（参见次年Bourbaki讨论班关于 Thurston 工作的报告）。

Thurston 证明映射环面上存在双曲结构的论文首页。该项工作把三维流形的双曲结构、Riemann 曲面、分形、填充二维区域的连续曲线等众多领域联系了起来。

故事六

石溪会议，1978 年夏

在石溪举行了一次关于Klein 群的盛大会议。Bill 出席了会议，但没有发言。Gromov 和我邀请他即兴做一个计划之外的长时间的报告。这是一场通向双曲三维流形无穷远端、凸包、皱褶曲面、ending lamination 等等的美妙旅程。在报告的过程中，Gromov 凑过来跟我说，Bill 这次报告使他感觉这个方面的研究还没真正开始。

凸包与皱褶曲面。双曲球体表面有一条分形曲线，粉红色与浅绿色的两个皱褶曲面围住的部分是该分形曲线在双曲球体内部的凸包，作为凸包边界的皱褶曲面在除了一个零测集之外都是测地曲面。| 图片来源：http://vivaldi.ics.nara-wu.ac.jp/~yamasita/

故事七

科罗拉多，1980 年 6 月至 1981 年 8 月

Bill 和我一起在 Boulder 大学做 Ulam 访问教授，在那里举办两个讨论班：一个较大的讨论班是把整个双曲性定理的全部证明细节过一遍，另一个较小的讨论班是关于Klein 群的动力系统以及一般性的动力系统。参加第一个讨论班的许多研究生们共同检查了双曲性定理的全部证明细节。

有一天，在动力系统的讨论班上，Thurston 迟到了。Dan Rudolph 正在精力充沛地对一个以往证明过程极度复杂的定理作简化证明。这个简化的证明在一小时之内就能讲完。在两个遍历的保测度变换的轨道相差不太远的前提下，该定理能把轨道等价类加强成共轭类。旧的证明 Katznelson、Ornstein 和 Weiss 用了一门短课才能解释清楚，而新证明的引人注目之处在于仅仅用一小时就能完成。Thurston 终于来了，问我前面讲了什么，让我帮他跟上进度。我都照办了。

在讲座即将结束的时候，Thurston 大声向我耳语：证明的难点究竟在哪里？我向他发出“嘘”声让他安静，提醒他应该尊重课堂环境。最后，Bill 说，只要想象一下：在一根线上布满了珠子；珠子往线的两端无穷地延伸，中间只有有限的间隙；然后让它们都滑向左边（同时他张开出双臂给我作形象的说明）。只要把这个想法翻译成标准的文字，就马上能给出一个新的证明。那天晚些时候，Dan Rudolph 充满敬畏地跟我说，他之前没有想象到 Bill Thurston 会聪明到这个程度。

故事八

美国加州 La Jolla 与巴黎，1981 年夏末

在科罗拉多的经历很愉快。Thurston 的几何讨论班在完全放松的氛围中度过。某一天我们构想出了 8 种几何模型，另一天我们为某个对象究竟应该命名为“manifold”还是“orbifold”而投票。我也正在写几篇我自己的关于 Hausdorff 维数、动力系统、极限集的测度的论文。接下来的夏天末尾，Thurston 回到普林斯顿。我则从巴黎飞到 La Jolla，给美国数学学会做一系列关于动力系统最新进展的特邀报告。为了达到更好的演讲效果，我决定改变报告的主题，换成首次向数学界公开展示整个双曲性定理！并且我也希望以此作为 Boulder 讨论班结束后我给自己安排的一次期末考试。

在去往美国的飞机上，我只准备了一页纸的概括性讲稿。但将要讲的报告却一共安排了四到五天，每天两场！第一天估计能勉强应付过去。我想：先讲点综述，剩下的再即兴发挥一下吧。但是想把这么重要的一系列报告做好，我需要极好的运气。历史性的时刻到了！

从巴黎到加州有 9 个小时的时差。刚到达的那天深夜我睡不着，到安排给我的办公室里准备报告的内容。很快我却发现，关于双曲性的论证过程，我碰到很多问题都没法自行解答。这时我发现办公室桌上的电话居然还可以打长途。此刻加州的时间是凌晨 4 点，普林斯顿的时间是早上 7 点。我打电话到 Thurston 的家，他接了。我向他陈述了我的问题，他先给出部分简短的回答。我赶快用笔记下来。他说等送完小孩到学校再赶回办公室之后给我回电话。当他在两个半小时之后打电话给我时，我对他刚才的答案提出更多否定意见，而他又作出更加细致的答复。我们终于把所有可能产生问题的地方都处理完毕。

加州时间 8 点整，我准备好了两场演讲的材料。第一天顺利度过：第一场报告，午餐，去沙滩，游泳，第二场报告，晚餐，告别同事，回住处睡觉。重新看报告的录像时我才发现，听众的阵容强大得可怕：Ahlfors，Bott，陈省身，Kirby，Siebenmann，Edwards，Rosenberg，Freedman，丘成桐，Maskit，Kra，Keen，Dodziuk……

来听这次报告的人。作开场介绍的是德高望重的 Ahlfors。听众里包含了当时几何与拓扑领域几乎所有的顶尖数学家。

Bill 和我每天重复这样的事情，配合得很完美。每天加州时间早上 8 点的时候，我准备好我的两场报告内容，做好一切提问的应对。当陈述 Bill 那些绝妙地控制住测地线长度的技术时，演讲推向高潮！这些测地线是分支皱褶曲面在分支处的曲线。要估计它们的长度，利用的却是内蕴曲面上测地流产生的动力系统的熵。这个熵又与分支曲面万有覆盖的面积增长率有关。但在负曲率的空间中，这个面积的增长速度却又被双曲球体的体积增长率所控制。证毕！不但如此，Thurston 还构造出一个漂亮的例子，表明估计的界是精确的。对于听众之一的 Harold Rosenberg（他是来自巴黎的精明的朋友）来说，这次报告的水平是超乎想象的。报告结束之后，他沮丧地问我：“Dennis，你是不是一直把 Thurston 锁在你办公室的楼上呀？”

Sullivan 阐述控制测地线长度绝妙证明的时刻。

我之前一直对这些报告背后的故事三缄吾口，直到现在才说出来。这一系列报告都被 Micheal Freedman 用录像机记录了。如今这些 Thurston-Sullivan 讲座的视频都能在互联网上找到。

故事九

巴黎，1981 年秋

我在美国数学学会的演讲大获成功之后，Bill 来巴黎访问我。我在私人办公室买了个舒适的沙发床，以便于他休息。他很有礼貌地问了我以下两个问题：一、如果之前在美国数学学会的演讲上没有把报告的主题换成他的双曲性定理的话，我原定计划讲的是什么内容；二、在科罗拉多，除了双曲性定理的讨论班之外，我似乎还在一直忙着别的东西，具体是在研究什么。

关于这些，我总共有 6 篇计划中论文的内容要告诉他。其中包括一个我从他那里学到的最吸引人的想法：对于无穷远球面上一个适当的集合来说，从双曲球体内部一点看过去时，在视觉上的 Hausdorff 测度，能定义出一个双曲三维空间中 Laplace 算子对应于本征值 f(2-f) 的大于零的本征函数。我向他陈述并解释这些想法。每当我陈述完一个想法，他就马上给出一个证明，或者我给出我证明的主要思路。这六篇论文里的定理都被我们一一证明，有的是他证，有的是我证。我们差点漏掉一种情形：如果最后一个本征函数 f>1 的话，规范化之后新的本征函数的平方积分范数将可以通过凸核的体积来估计。Bill 躺回沙发床中，闭上双眼想了没多久，就很快把差点漏掉的这种情形证明了出来。他估计的方法是让测地线无限延长，然后在横截的方向求平均值。

随后我们外出散步，从 Orleans 港穿过巴黎市区走到 Clignancourt 港。我们边走边沉浸在数学讨论之中，以致于忘了自己身处何地。一直等到我们经过塞纳河，圣母院和古监狱同时映入眼帘时，才想起来自己置身于美丽的巴黎。

故事十

从普林斯顿到曼哈顿，1982-1983

由于开始了长达 13 年的纽约市立大学 Einstein 研讨班的主持职务，我不得不把时间分配开，一直在法国高等科学研究院和纽约市立大学研究生中心之间来回奔波。Einstein 研讨班的主题一开始是动力系统与拟共形同胚，后来慢慢转变成拓扑中的量子对象。Bill 则继续发掘和训练有天赋的学生，传播双曲空间那些漂亮的理论，培养出大批新一代年轻的几何学家。Bill 推迟写他那关于双曲性定理论文的终稿。取而代之的，是让他不断培养起来的越来越多的新一代几何学家们把整套理论发展到更加广阔的天地中去。他在 20 世纪 70 年代初关于叶状结构的论文震撼了该领域，但同时也终结了该领域的研究。他不想看到在双曲几何领域发生同样的事情。

有一次，我们准备在曼哈顿聚一下，讨论在单变量复动力系统、双曲几何，以及我之前研究的 Klein 群的各种类比。在公寓里我们很随意地讨论，讨论话题也开始拓展延伸。最后我们在 Bill 乘火车回普林斯顿之前 30 分钟制定好了研究计划。我概括了一般性的类比：庞加莱极限集、不连续域、复结构的形变、刚性定理、分类空间、Ahlfors 有限性定理、Ahlfors 与 Bers 的工作……与以下概念相比较：Julia 集、Fatou 集、非游荡域定理、Hubbard 与 Douady 的工作……他快速完整地吸收了这些想法，然后离开去坐火车。

两周之后，我们听说他用 Teichmüller 空间上不动点的观点改写了整个复动力系统的理论，其中的部分手法与他的双曲性定理异曲同工。若干年后许多新的结果相继涌现，比如 McMullen 的工作。自此，复动力系统的研究提升到了一个更高的水平。

后 记

在 2011 年 Banff 举行的 Jack Milnor 的 80 岁寿宴上，我和 Bill 再次相遇。在 30 年之后，我们从之前研究中断的地方重新开始。（当我第二次见到他的绿色格子衬衫时，我称赞这件衣服，第二天他就把衣服送给了我。）我们还约定一起去攻克 Klein 群和复动力系统框架里遗留下来的一个大问题：不变线场猜想。这是一个好主意，不幸的是，它永远都不可能实现了。

Thurston 在 Banff 的会议上讲解多项式迭代与熵之间的联系。

在那次会议上，当 Jeremy Kahn 报告他和 Markovic 合作的对长达数十年之久的子曲面猜想作出的证明的时候，Bill 小声对我说：“我忘了取偏移这一步了。”在 Kahn-Markovic 的证明中，需要把所有可能的理想三角形粘起来，构造出浸入的曲面，然后把遍历理论应用到在这个空间的作用上。当两个理想三角形沿着一条边粘合时，各自的中心在粘合的边上的垂足也许并不吻合，而是可以差了一个偏移量。这一步偏移保证了取极限时不遗漏任何东西，这也正是 Bill 之前的证明里漏掉的。我带着极为愉快的心情看到 Kahn 和 Markovic 完成了证明。证明的每一步都让我回忆起 30 多年前 Bill 发明的类似关键思想与技术。这些思想与技术都传递到他在普林斯顿的门徒们那儿了。

同一次会议上 Kahn 讲解他与合作者的技术。

本文英文原文出自Notices of the A.M.S.，2015 年 11 期。中文翻译曾发表于杜晓明科学网博客，此文为最新修订版，原文题目为“沃尔夫奖得主Sullivan：菲尔茨奖得主Thurston的十个故事”，现标题为编者所加。原文链接：https://www.ams.org/journals/notice

维灵顿·德梅洛：巴西动力系统理论的先驱

维灵顿·塞尔索·德梅洛（Welington Celso de Melo，1946-2016）是20世纪后半叶巴西数学界的杰出代表，以其在动力系统理论，特别是实一维动力系统和单峰映射重整化研究方面的开创性工作而闻名于世。这位严谨而富有洞察力的数学家不仅推动了数学理论的发展，还培养了一批优秀的学生，其中包括菲尔兹奖得主阿图尔·阿维拉。

早年生活与教育

维灵顿·德梅洛于1946年11月17日出生在巴西米纳斯吉拉斯州的小镇瓜佩。他在巴西接受了早期教育，后来进入里约热内卢的巴西纯数学与应用数学研究所（IMPA）深造。在IMPA，他有幸师从动力系统领域的另一位巴西数学巨匠雅各布·帕利斯（Jacob Palis），并于1970年代初期获得博士学位。

学术生涯与主要贡献

德梅洛的整个职业生涯几乎都与IMPA紧密相连。1980年，他成为该研究所的正式教授，并一直在此工作直至2016年去世。他的研究主要集中在动力系统理论，这是研究随时间演化的系统的数学分支。

实一维动力系统的拓扑行为：德梅洛与马可·马滕斯（Marco Martens）和塞巴斯蒂安·范斯特里恩（Sebastian van Strien）合作，对一维实动力系统的拓扑行为进行了全面描述。这项工作为理解简单系统中复杂动力学行为奠定了基础。

单峰映射的重整化理论：他与阿尔贝托·平托（Alberto Pinto）和埃德森·德法利亚（Edson de Faria）合作，证明了Cr单峰映射重整化的全局双曲性。这一重要结果为重整化理论提供了严格的数学基础，该理论在统计物理和量子场论中也有广泛应用。

数学严谨性：德梅洛以极端严谨的数学风格著称。他坚持最高标准的数学证明，这种严谨态度使他的工作具有极高的可信度和持久价值。1998年，他在柏林国际数学家大会上发表了题为”一维动力系统中的刚性与重整化”的演讲，总结了他在这方面的研究成果。

教学与学术影响

尽管德梅洛以严格著称，甚至”吓到”了一些学生，但他实际上是一位非常支持和鼓励年轻数学家的导师。最著名的例子是他与菲尔兹奖得主阿图尔·阿维拉的关系。阿维拉最初因为德梅洛的严格名声而不敢正式选修他的课程，只是旁听。然而，德梅洛很快发现了这位年轻学生的才华，并给予了他极大的鼓励和支持。这种师生关系最终促成了巴西数学的又一次辉煌。

德梅洛还指导了许多其他学生，并在IMPA建立了一个活跃的研究小组，使巴西在动力系统领域保持了国际领先地位。

荣誉与奖项

德梅洛的贡献获得了多项国际认可：

• 2003年第三世界科学院奖（TWAS Prize）
• 巴西科学院院士
• 多个国际学术机构的特邀演讲者和访问教授

个人生活与遗产

德梅洛于2016年12月21日逝世，享年70岁。即使在休闲时间，如帆船运动时，他也在思考数学问题。他留下的不仅是重要的数学成果，还有培养新一代数学家的传统。正如阿图尔·阿维拉所回忆的，德梅洛虽然以严格著称，但实际上对学生非常友善和支持。

维灵顿·德梅洛的工作将巴西数学推向了国际舞台，他的遗产继续影响着全球的动力系统研究。他对数学严谨性的坚持和对年轻数学家的培养，为巴西数学界树立了高标准，确保了该国在这一领域的持续繁荣。

阿图尔·阿维拉：开创拉丁美洲动力系统的菲尔兹奖得主

阿图尔·阿维拉·科尔德罗·德梅洛（Artur Avila Cordeiro de Melo）是当代数学界最杰出的学者之一，以其在动力系统和谱理论领域的开创性工作闻名于世。这位巴西数学家于2014年获得菲尔兹奖，成为首位获此殊荣的拉丁美洲和葡语国家数学家，标志着全球数学研究版图的重要扩展。

早年经历与教育背景

阿维拉于1979年6月29日出生在巴西里约热内卢，自幼展现出非凡的数学天赋。他的父亲是一位自学成才的会计师，在阿维拉三岁时就教会了他读写和基础数学。五岁时，阿维拉已经开始自学阅读数学书籍，展现出超前的学习能力。

1995年，年仅16岁的阿维拉在国际数学奥林匹克竞赛中获得金牌，这一成就为他赢得了巴西纯数学与应用数学研究所（IMPA）的奖学金。值得注意的是，他在攻读硕士学位期间仍在里约热内卢的圣本笃学院和圣阿戈斯蒂尼奥学院完成高中学业。

学术生涯与主要成就

阿维拉的学术道路堪称传奇。19岁时，他开始撰写关于动力系统理论的博士论文，并于2001年在IMPA获得博士学位，导师是著名数学家维灵顿·德梅洛（Welington de Melo）。同年，他前往法国进行博士后研究，师从1994年菲尔兹奖得主让-克里斯托夫·约科兹（Jean-Christophe Yoccoz）。

“十马丁尼问题”的解决：2005年，26岁的阿维拉与斯维特拉娜·吉托米尔斯基（Svetlana Jitomirskaya）合作，解决了由美国数学物理学家巴里·西蒙（Barry Simon）提出的”十马丁尼问题”。这个困扰学界25年的难题探讨了特定类型算子在给定参数条件下的谱是否为康托集。马克·卡克（Mark Kac）曾承诺为解决问题者提供十杯马丁尼作为奖励，阿维拉和吉托米尔斯基最终给出了肯定的答案。

Zorich-Kontsevich猜想的证明：同年，阿维拉与马塞洛·维亚纳（Marcelo Viana）合作证明了Zorich-Kontsevich猜想，该猜想涉及紧致黎曼曲面上阿贝尔微分模空间上Teichmüller流的非平凡Lyapunov指数的性质。

动力系统理论的革新：阿维拉的工作彻底改变了动力系统领域的研究面貌。他利用重整化这一强大思想作为统一原则，在一维和复动力系统、薛定谔算子的谱理论、平坦台球和部分双曲动力学等方面做出了基础性贡献。

学术职位与国际影响

阿维拉在学术机构间保持着独特的合作模式：

• 2003年起担任法国国家科学研究中心（CNRS）研究员，2008年成为该中心最年轻的研究主任
• 2018年9月起任苏黎世大学教授
• 同时保持与IMPA的紧密联系，每年在巴西和法国各工作半年

这种跨国工作模式使他成为连接欧洲和拉丁美洲数学研究的重要桥梁。

荣誉与奖项

阿维拉的卓越贡献获得了国际数学界的广泛认可：

• 2014年菲尔兹奖：数学界最高荣誉，表彰他在动力系统领域的革命性贡献
• 2011年迈克尔·布林动力系统奖：表彰他在动力系统理论方面的杰出工作
• 2008年欧洲数学学会奖：肯定他在数学研究上的卓越成就
• 2006年塞勒姆奖：表彰他在调和分析及相关领域的贡献
• 2015年法国荣誉军团骑士勋章：法国最高荣誉之一
• 2019年当选美国国家科学院外籍院士：国际科学界的崇高荣誉

学术风格与个人特质

阿维拉以其深刻的洞察力和独特的解决问题方式著称。他曾在采访中提到：”很多时候，我寻找已知的难题并努力解决它们。但我也致力于构建和发展理论，这有时不仅涉及解决问题，还包括问题的表述。”这种理论构建与问题解决相结合的方法，使他的工作既有广度又有深度。

尽管成就卓著，阿维拉保持着谦逊的态度。他回忆自己最初因德梅洛教授的严格名声而不敢正式选修其课程，只是旁听，这一经历展现了他作为学习者的一面。如今，他自己也成为新一代数学家的榜样和导师。

对巴西及拉丁美洲数学的影响

阿维拉的成功对巴西和整个拉丁美洲的数学发展产生了深远影响：

1. 激励作用：作为首位获得菲尔兹奖的拉丁美洲数学家，他证明了该地区的学者也能达到数学研究的最高水平
2. 国际合作：他的跨国工作模式促进了巴西与欧洲顶尖数学机构的交流
3. 教育推动：他的成功故事激励了无数拉丁美洲年轻人投身数学研究

阿维拉曾表示：”我来自一个数学传统并不强大的国家，这让我更加意识到在全球范围内推广数学的重要性。”这种使命感使他不仅是一位杰出的研究者，也成为数学教育和发展的重要倡导者。

当前研究与未来方向

近年来，阿维拉继续在动力系统理论的前沿开展工作。2017年，他在雅盖隆大学发表了题为”单频薛定谔算子与几乎可约性猜想”的Łojasiewicz讲座。2019年，多伦多菲尔兹研究所举办了以他命名的研讨会，探讨他工作的当前和潜在影响。

阿维拉的研究继续关注动力系统中的基本问题，如混沌行为的数学描述和长期预测的可能性。他在2019年菲尔兹研讨会上的公开演讲”应对混沌”中，反思了这一领域的历史演变和未来挑战。

阿图尔·阿维拉的故事不仅是个人天才的胜利，也是全球数学共同体多样性和包容性的证明。他的成就打破了地域限制，证明数学卓越可以来自世界任何角落。作为研究者、导师和榜样，阿维拉继续影响着数学的未来发展，他的遗产将激励几代数学家追求科学真理的最高境界。

曼弗雷多·多·卡莫：巴西微分几何学派的奠基者

曼弗雷多·佩尔迪冈·多·卡莫（Manfredo Perdigão do Carmo，1928-2018）是20世纪巴西最具影响力的数学家之一，被誉为”巴西微分几何的元老”。他通过开创性的研究、经典教材的撰写和杰出学生的培养，将巴西推上了国际微分几何研究的版图。多·卡莫的学术生涯跨越半个多世纪，其贡献不仅体现在理论研究中，更在于他建立了一个繁荣的数学学派。

早年生活与教育背景

多·卡莫于1928年8月15日出生在巴西东北部阿拉戈斯州的马塞约。1947年至1951年间，他在累西腓大学（现伯南布哥联邦大学）攻读土木工程，这一选择反映了当时巴西对应用学科的重视。毕业后，他短暂从事工程师工作，但很快转向数学教育。

1959年，在数学家埃隆·利马（Elon Lages Lima）的建议下，多·卡莫前往里约热内卢的巴西纯数学与应用数学研究所（IMPA）深造。这一决定改变了他的人生轨迹，也深刻影响了巴西数学的发展方向。1960年，他赴美国加州大学伯克利分校攻读博士学位，师从微分几何大师陈省身（Shiing-Shen Chern），并于1963年完成题为《某些凯勒流形的上同调环》的博士论文。

学术生涯与机构贡献

多·卡莫的职业生涯与IMPA紧密相连。1966年，他成为该研究所的教授，2003年起担任荣誉教授，直至2018年4月30日以89岁高龄在里约热内卢去世。IMPA作为拉丁美洲顶尖的数学研究机构，为多·卡莫提供了理想的研究环境，而他也为提升该机构的国际声誉做出了重要贡献。

在IMPA期间，多·卡莫不仅专注于个人研究，还积极参与学术管理。1971-1973年间，他担任巴西数学学会主席，推动国内数学教育的发展和国际交流的扩大。他的领导帮助巴西数学界建立了与全球顶尖学者的联系网络。

研究贡献与学术影响

多·卡莫的研究主要集中在黎曼几何和曲面微分几何两大领域，他在以下几个方面做出了开创性贡献：

等距浸入的刚性与凸性

多·卡莫与F.华纳（F. Warner）合作研究了球面中超曲面的刚性与凸性问题。他们1969年发表在《微分几何杂志》上的论文《球面中超曲面的刚性与凸性》成为该领域的经典文献，为理解高维空间中曲面嵌入的性质奠定了基础。

极小曲面的稳定性

多·卡莫对极小曲面的稳定性研究尤为深入。他与J.L.巴博萨（J.L. Barbosa）合作的一系列工作建立了关于稳定极小曲面尺寸限制的重要结果。1978年，他在赫尔辛基国际数学家大会上作特邀报告，题为”极小曲面：稳定性与有限性”，总结了这一领域的研究进展。

常平均曲率流形

多·卡莫对常平均曲率流形的研究开辟了新的方向。他与M.达伊泽尔（M. Dajczer）合作研究了旋转超曲面在常曲率空间中的性质，这些成果发表在《美国数学会会报》等重要期刊上，为理解特殊曲面的几何性质提供了新工具。

流形拓扑与等周问题

多·卡莫对开放流形的里奇曲率与拓扑关系的研究，以及他与J.L.巴博萨合作的关于一般等周不等式的工作，都体现了他在几何分析领域的广泛兴趣和深刻洞察。

多·卡莫一生发表了100多篇经过同行评审的论文，2012年，施普林格出版社精选了他的部分重要论文结集出版，彰显了其工作的持久影响力。

经典教材与数学教育

多·卡莫对数学的贡献不仅体现在研究上，更在于他撰写的几部影响深远的教材：

1. 《曲线与曲面的微分几何》（1976）：这部经典教材已被翻译成多种语言，被哈佛大学、哥伦比亚大学等世界顶尖学府采用为课程教材。该书以清晰的叙述和精心设计的习题著称，培养了几代微分几何学者。
2. 《黎曼几何》（1992）：系统介绍了黎曼几何的基本概念和定理，成为研究生阶段的标准参考书。
3. 《微分形式及其应用》（1994）：为高年级本科生和研究生提供了微分形式的现代处理方法。

这些教材的共同特点是概念清晰、证明严谨、循序渐进，反映了多·卡莫对数学教育的深刻理解。他曾在采访中提到：”写教材时，我总是试图站在学生的角度思考，想象他们会遇到什么困难。”

学术传承与学生培养

多·卡莫指导了27名博士生，其中包括塞索·科斯塔（Celso Costa，发现科斯塔极小曲面）、马科斯·达伊泽尔（Marcos Dajczer）和凯蒂·特南布拉特（Keti Tenenblat）等著名几何学家。这些学生延续了他的学术风格，形成了巴西微分几何学派的中坚力量。

多·卡莫的指导风格以严谨著称。他的学生回忆道：”他从不轻易放过任何不严谨的论证，这种严格标准使我们终身受益。”同时，他也给予学生充分的自由探索空间，鼓励他们发展自己的研究兴趣。

荣誉与奖项

多·卡莫的学术成就获得了广泛认可：

• 古根海姆奖学金（1965, 1968）：两次获得这一著名研究资助
• 阿尔瓦罗·阿尔贝托上将奖（1984）：巴西科学技术领域的最高荣誉之一
• TWAS数学奖（1992）：第三世界科学院颁发的国际奖项
• 巴西国家科学功绩勋章（1995）：表彰他对巴西科学发展的杰出贡献
• 美国数学会会士（2012）：国际数学界的崇高荣誉

此外，他还获得了阿拉戈斯联邦大学（1991）和穆尔西亚大学（2012）的荣誉博士学位，并被选为巴西科学院院士（1970）和第三世界科学院院士（1997）。

学术遗产与影响

多·卡莫去世后，巴西数学界失去了一个标志性人物，但他留下的遗产仍在持续发挥作用：

1. 巴西微分几何学派：他培养的学生和学生的学生形成了一个强大的研究群体，使巴西在微分几何领域保持国际领先地位。
2. 教材的持久影响：他的著作继续被全球各地的大学采用，每年都有新的数学学子通过这些教材进入几何学的殿堂。
3. IMPA的国际声誉：多·卡莫的工作帮助IMPA成为世界级的数学研究中心，吸引了来自全球的优秀学者。

2021年，《圣保罗数学科学杂志》出版了纪念多·卡莫的特刊，编者在前言中写道：”多·卡莫不仅是一位杰出的数学家，更是巴西科学界的灯塔，他的严谨、正直和对数学的热爱激励了我们所有人。”

曼弗雷多·多·卡莫的一生展现了纯粹数学研究的持久价值。从巴西东北部的土木工程学生到国际知名的几何学家，他的故事证明了数学无国界，天才可以在任何环境中绽放。通过研究、教学和学术领导，多·卡莫为巴西和世界的数学发展做出了不可磨灭的贡献，他的精神继续激励着追求数学真理的新一代学者。

你能够想象一位东京大学的数学博士是日本电视艺人吗？这听起来似乎不太可能，但鹤崎修功却打破了这种常规，将严谨的数学思维与娱乐性十足的电视节目完美结合，成为了日本综艺节目《东大王》中的常驻嘉宾，并且连续6年稳居节目中的顶尖选手。这样一位跨界人物，能够将学术领域的深奥数学与大众化的娱乐形式结合，正是本书《原来数学这么有用》的独特魅力所在。

1. 学术与娱乐的完美结合：一本让你爱上数学的书

鹤崎修功的这本《原来数学这么有用》，不仅仅是一本讲解数学概念的书籍，更像是一场跨越学术与日常生活的思维旅行。在这本书中，作者以一种通俗易懂且引人入胜的方式，将数学的奥秘从教科书里带到了每个人的生活中。无论是通过大数的浪漫，还是揭示数学思维在日常生活中的无限便利，书中每个章节都渗透着数学与生活的紧密联系。数学不再是冷冰冰的公式，而是与我们的日常息息相关的一部分——从概率判断到逻辑推理，再到复利法则的应用，数学思维像一把钥匙，帮助我们解锁生活中的种种谜题。

2. 让数学不再高冷：不只是公式的背诵

与一般的数学书籍不同，鹤崎修功的这本《原来数学这么有用》并不以枯燥的公式和定理为主，而是通过许多生活中的例子和趣味性的讲解，使读者能够在轻松的氛围中理解数学的内涵。比如通过简单易懂的”维恩图”，让我们了解如何掌握整体情况；通过“反证法”帮助我们理清思维，找出难题的突破口。而且，作者还巧妙地通过历史故事将数学家们的经历和挑战呈现出来，这些天才人物的故事不仅丰富了书的内容，也给读者带来了不同于传统教科书的情感连接。

3. 从娱乐节目到数学殿堂：读这本书，你会重新定义“数学”

鹤崎修功的身份不仅仅是一名学者，他还是日本综艺节目《东大王》的冠军和常驻嘉宾。正是这种双重身份让他能够从不同的角度去看待数学：一方面是严谨的学术研究，另一方面则是通过娱乐的方式传播数学的乐趣。因此，这本书不仅适合学生和数学爱好者，更适合任何想在繁忙生活中找到一点数学趣味的读者。书中的附录部分特别适合文科生和数学基础薄弱的读者，通过简洁明了的计算技巧，让你在轻松中掌握数学的小窍门。这种“学以致用”的思维，让《原来数学这么有用》成为一本真正能够为普通读者带来实际价值的数学入门书籍。

4. 数学家与工作者的小故事：从毕达哥拉斯到鹤崎修功

《原来数学这么有用》不仅仅是一本介绍数学原理的书，它还融入了许多数学家和数学工作者的动人故事，带领读者走进数学的历史与人性。书中的每一位数学家，不论是远古的毕达哥拉斯，还是近现代的拉马努金、费马，甚至是书中的作者鹤崎修功自己，都通过独特的故事展现了数学世界的多样性与魅力。

例如，书中提到毕达哥拉斯，他不仅是数学的奠基人之一，还是一位哲学家和宗教改革者。毕达哥拉斯的“数学即美”的理念影响了后来的数学发展，他将数字与和谐美的关系融入了音乐、天文学等多个领域。费马的“费马大定理”则成为了数学史上最著名的难题之一，这一难题直至1994年才被证明，书中讲述了费马的简短批注以及他对于数学的热情，令人感受到数学探索中的孤独与坚持。鹤崎修功作为本书的作者，也通过自己跨越学术与娱乐的故事，讲述了数学家如何在现代社会中实现自我价值，他的亲身经历让读者明白，数学不仅是一种知识，也是一种思维方式，能够塑造人的世界观。

结语

《原来数学这么有用》不仅仅是一本数学书，它也成为了跨界传播数学思想的桥梁。在娱乐和学术的双重身份之间，鹤崎修功给我们呈现了一个更为生动和多元的数学世界。数学不再只是抽象的符号，而是走进了每个人的生活，帮助我们理解世界的规律和秩序。如果你也曾为枯燥的数学课感到头痛，那么不妨翻开这本书，感受数学在你生活中的美丽与实用。

我们生活的世界充满了复杂的形状：蜿蜒曲折的海岸线、崎岖不平的山脉、枝繁叶茂的树木、变幻莫测的云朵、人体内错综复杂的血管网络…这些形状无法用传统的欧几里得几何（点、线、圆、球、立方体等）来精确描述。它们往往显得“粗糙”、“破碎”、“不规则”，并且在不同的尺度下观察，似乎总能发现新的、相似的细节结构。为了描述和研究这种无处不在的复杂性，一门新的几何学应运而生——这就是分形几何。

一、 什么是分形？

“分形”（Fractal）一词由数学家本华·曼德布罗特（Benoît B. Mandelbrot）在1975年根据拉丁语“fractus”（意为“破碎的”、“不规则的”）创造。虽然很难给出一个涵盖所有情况的精确定义，但分形通常具有以下核心特征：

1. 精细结构： 无论你将其放大多少倍，分形总是展现出丰富的细节。它没有传统意义上的“光滑”表面或边界。

2. 自相似性： 这是分形最显著的特征之一。它指的是分形的局部（一个小的部分）在形态、结构或统计特性上与整体相似。这种相似性可以是：

• 精确自相似： 如科赫曲线（Koch curve）、谢尔宾斯基三角形（Sierpinski triangle）。每个小部分都是整体的精确缩小复制品。
• 近似自相似： 如海岸线、山脉。整体和局部在统计特性（如粗糙度）上相似，但并非完全相同的几何形状。
• 统计自相似： 在不同尺度下，分形的某些统计特性（如起伏的方差）保持不变。

3.分数维数： 这是分形区别于经典几何的关键数学特征。经典几何中，点是0维，线是1维，面是2维，体是3维。分形则具有非整数的维数（分数维）。例如：

• 科赫曲线：其长度在无限放大下趋于无穷，但又不填满一个平面，其豪斯多夫维数约为1.262。
• 康托尔集：一个在[0,1]区间内挖去中间三分之一，再对剩余部分不断重复此操作得到的点集。它长度为零（1维测度），但点数无限（0维测度不够），其豪斯多夫维数约为0.631。
• 谢尔宾斯基地毯：其面积为零（2维测度），但结构无限复杂，豪斯多夫维数约为1.893。
• 分数维数量化了分形填充空间的能力和其不规则性的程度。常见的分数维计算方法包括豪斯多夫维数（Hausdorff dimension）和计盒维数（Box-counting dimension）。

二、 分形的诞生与发展

虽然自然界的分形现象早已存在，但分形几何作为一门系统的数学学科，其奠基主要归功于曼德布罗特。他在20世纪60-70年代的工作，特别是1982年出版的巨著《大自然的分形几何学》（The Fractal Geometry of Nature），极大地推动和普及了分形几何。

• 先驱者： 在曼德布罗特之前，一些数学家已经构造出了具有分形特性的“怪物曲线”，如皮亚诺曲线（Peano curve，能填满正方形）、希尔伯特曲线（Hilbert curve）、冯·科赫曲线（von Koch curve）、康托尔集（Cantor set）、魏尔斯特拉斯函数（处处连续但无处可导）等。但这些在当时多被视为数学上的“病态”反例，并未被系统地联系到自然界的形态。
• 曼德布罗特： 曼德布罗特的关键贡献在于认识到这些“病态”结构恰恰是描述自然界中普遍存在的复杂、不规则形状的理想工具。他研究了棉花价格波动、尼罗河洪水、星系分布、海岸线长度等问题，发现它们都具有尺度不变性和统计自相似性。他提出“英国的海岸线有多长？”这个著名问题，揭示了测量结果依赖于测量尺度的分形本质。
• 计算机图形学的推动： 计算机技术的发展使得复杂分形结构的可视化和计算成为可能。曼德布罗特集（Mandelbrot set）和朱利亚集（Julia set）等复动力系统产生的精美分形图像，极大地吸引了公众和科学家的兴趣，展示了数学惊人的美学价值。

三、 如何生成分形？

分形可以通过多种数学方法生成：

1. 迭代函数系统： 这是生成分形（尤其是严格自相似分形）最常用和强大的方法之一。它基于一个几何变换集合（通常是收缩仿射变换，如缩放、旋转、平移），反复应用这些变换到一个初始集合（如一条线段、一个三角形）上。每次迭代都将变换作用到前一步的结果上。在无限次迭代后，结果会收敛到一个唯一的、不依赖于初始集的极限图形——即吸引子（Attractor），这个吸引子通常是一个分形。著名的谢尔宾斯基三角形、科赫曲线、巴恩斯利蕨（Barnsley fern）等都是用IFS生成的。
2. 复动力系统： 对复平面上的简单函数（如 f(z)=z2+c ，其中 z 和 c 是复数）进行反复迭代。对于不同的初始点 z0 和参数 c ，其轨道行为（趋向无穷或保持有界）会形成极其复杂的边界。朱利亚集（Julia set）是使得迭代行为不稳定的点集边界。曼德布罗特集（Mandelbrot set）则是参数 c 的集合，使得从 z0=0 开始的迭代序列保持有界。这些集合都是具有精细结构和分数维数的著名分形。
3. L-系统（林德迈耶系统）： 主要用于模拟植物的生长。它基于一组符号（代表植物的组成部分，如茎、叶）和一组重写规则（规定符号如何被替换）。通过迭代应用这些规则，一个简单的初始字符串（“公理”）会演化成复杂的、具有自相似性的字符串，再通过图形解释（如“画线”、“转向”）就能绘制出分形植物。
4. 随机分形： 在确定性规则（如IFS）中加入随机性（如随机选择变换），可以生成更接近自然界不规则形态的分形，如山脉、云层、景观。布朗运动（Brownian motion）的轨迹本身也是一个分形（维数为2）。

四、 分形几何的应用

分形几何的应用范围极其广泛，几乎渗透到科学和工程的各个领域：

1.自然科学：

• 地理学/地质学： 模拟海岸线、河流网络、山脉地形、岩石裂缝分布、矿藏分布。
• 生物学/医学： 描述血管系统、支气管树、神经结构、蛋白质折叠、DNA序列、肿瘤形态、心电图/脑电图分析。
• 物理学： 研究湍流、材料断裂表面、多孔介质渗透性、电介质击穿、凝聚态物理中的相变和临界现象、等离子体。
• 化学： 胶体聚合、高分子结构、催化剂表面分析。
• 气象学： 云层结构、降雨分布模型。

2.工程技术：

• 计算机图形学： 生成逼真的自然景观（地形、植被、云、火、烟雾）、纹理合成、特殊视觉效果。
• 图像处理： 图像压缩（分形压缩利用图像的自相似性）、图像分析（纹理识别、边缘检测）。
• 信号处理： 分析具有长程依赖性或自相似特性的信号（如网络流量、金融时间序列）。
• 天线设计： 设计小型化、多频段的分形天线。
• 材料科学： 分析材料表面粗糙度、多孔材料结构、复合材料性能。
• 电子学： 设计分形电容器、电感器。

3.金融经济学： 分析金融时间序列（如股票价格、汇率）的波动特性（常具有分形特征和长记忆性）、风险管理。

4.艺术与设计： 分形艺术作为一种独特的数字艺术形式，创造出极具美感和复杂性的图像和动画。也应用于建筑设计、装饰图案设计。

五、 意义与未来

分形几何提供了一种全新的视角来观察和理解我们周围复杂、不规则的世界。它揭示了隐藏在混乱表象下的有序结构——尺度不变性和自相似性。分数维数则为我们提供了一种强大的量化工具来描述这些结构的复杂程度。

分形几何不仅是数学上的重大突破，更是连接数学与自然科学、工程技术乃至艺术的重要桥梁。它深刻地改变了我们对“形状”、“维度”和“复杂性”的传统认知。随着计算能力的提升和研究深入，分形几何必将在更多领域展现出其强大的描述、分析和创造能力，帮助我们更好地模拟自然、优化设计、理解复杂系统。这门描述“粗糙之美”的几何学，将继续拓展我们对宇宙和自身认知的边界。

结论先行：

1. 素数定理比黎曼猜想的难度低得多，都凝聚了很多大数学家的智慧，历经近百年才有结果；
2. 哪怕有个人能够证明存在常数 使得 这个区域内没有黎曼函数的零点，都是巨大的突破。

素数定理

先来介绍一下素数定理的发展历史。素数定理（Prime Number Theorem，PNT）是数论的核心成果之一，描述了素数分布的渐近规律。其发展历史跨越两个多世纪，凝聚了众多数学家的智慧。

高斯（Carl Friedrich Gauss，1792）在15岁时通过研究素数表发现：素数密度约为 ，于是提出猜想：（对数积分）。数学家勒让德（Adrien-Marie Legendre，1798）在《数论随笔》中提出经验公式：，首次尝试用解析方法逼近素数分布。

数学家切比雪夫（1850s）得到上下界证明：证明存在常数 使得： 具体值：，。他使用的关键工具是切比雪夫函数 ，并且证明 当且仅当 。

黎曼（1859）提出了黎曼 函数，并发表论文《论小于给定数值的素数个数》，定义： 。解析延拓至复平面（除 外全纯）。显式公式给出 的精确表达式（含黎曼函数的零点）： 。

著名黎曼猜想：若所有非平凡零点满足 ，则素数定理误差最优。

素数定理的最终证明（1896）：阿达玛（Jacques Hadamard） 与 德·拉·瓦莱-普桑（Charles de la Vallée Poussin）独立证明：（对 ），并推出： 。具体的方法：

1. 通过 的欧拉乘积和非零性，证明 在 解析。
2. 移动积分路径，控制误差项。

直到20世纪，才有素数定理的初等证明（1949）。塞尔伯格（Atle Selberg） 与 埃尔德什（Paul Erdős）：

• 塞尔伯格恒等式：
• 初等方法：仅用实数分析，避免复变函数。
• 争议：两人因证明优先权公开争论，但共享1950年菲尔兹奖（塞尔伯格）。

关于素数定理的精细化与推广，误差项优化包括

• 瓦莱-普桑（1899）：。
• 科赫（1901）：若黎曼猜想成立，则 。

历史意义

阶段	贡献者	关键突破
猜想	高斯、勒让德	发现 模式。
初等边界	切比雪夫	给出 的上下界。
复分析奠基	黎曼	揭示 零点与素数分布的联系。
严格证明	阿达玛、瓦莱-普桑	证明 推出 PNT。
初等证明	塞尔伯格、埃尔德什	不依赖复分析。
精细化	瓦莱-普桑、科赫、狄利克雷	优化误差项及推广到算术级数。

素数定理的重大意义与价值

1. 解析数论诞生：素数定理证明标志解析数论成为独立分支。
2. 黎曼猜想的基石：PNT 等价于 在 无零点，而黎曼猜想要求 。
3. 现代应用：PNT 是密码学（如 RSA 算法）和随机算法（如素性测试）的理论基础。

素数定理的发展史，是数学从实验观察走向严格分析，再回归初等本质的缩影，彰显了人类对素数奥秘的不懈探索。

黎曼猜想

黎曼猜想中关于 在直线 上无零点的结论，直接等价于数论中的核心定理——素数定理（Prime Number Theorem）。根据刚刚的陈述，素数定理描述素数分布渐近行为： 或等价形式 其中： 是不超过 的素数个数， 是切比雪夫函数（第二形式）。

在1896年，数学家阿达玛（Hadamard）和德·拉·瓦莱-普桑（de la Vallée Poussin）独立证明： 对所有实数 成立，这一结论直接推出素数定理。素数定理成立 在 上无零点（除 处的极点）。

证明思路（简要）

1. 通过 控制素数分布：
   利用 的欧拉乘积和解析延拓，将 表示为复积分：
2. 移动积分路径：
   若 在 无零点，可将积分路径移至 左侧，得到主项 和误差项。
3. 误差控制：
   无零点保证了积分在移动路径时无奇点干扰，最终推出：

4. 重要性

• 素数分布的基础：素数定理是解析数论的里程碑，解决了高斯和勒让德关于 的猜想。
• 黎曼猜想的弱形式：
  无零点比黎曼猜想（所有非平凡零点满足 ）弱得多，但已足以推出素数分布的主项。
• 误差优化：
  若黎曼猜想成立，素数定理误差可优化为 ，但无零点条件仅给出 。

在 无零点这一性质，本质是素数定理的复分析表述。它不仅是黎曼猜想的部分条件，更是解析数论中连接 函数零点与素数分布的桥梁。

黎曼猜想的零点与非零点区域

关于黎曼函数在实部小于1的区域（）中零点分布，有以下结论：

1. 平凡零点（Trivial Zeros）

• 黎曼函数在负偶数点（如 ）处有零点，这些零点称为平凡零点。
• 这些零点位于实轴上（），且是 区域内唯一的零点。

2. 非平凡零点（Non-trivial Zeros）

• 所有非平凡零点都位于临界带（）内。
• 黎曼假设（未证明）声称这些零点全部位于临界线 上。

3. 无零点的区域

以下区域在的范围内没有零点（包括平凡和非平凡零点）：

• 且 （为正整数）：除负偶数（平凡零点）外， 的区域没有其他零点。
• 函数方程 表明，若 是零点，则 也是零点，但平凡零点仅在负偶数处。
• ：Hadamard和de la Vallée Poussin证明 对所有实数 成立，这是素数定理证明的关键步骤。
• 临界带内接近 的区域：存在一个零自由区域：，其中 是常数。

4. 关键结论

• ：无零点（欧拉乘积收敛且非零）。
• 且 ：无零点（仅负偶数有平凡零点）。
• ：无零点（素数定理）。
• 临界带内但满足 的区域无零点。尽管，但这条曲线在无穷远处趋近于1。

非平凡零点仅可能存在于临界带内不满足上述零自由条件的区域（即 ），但黎曼假设认为它们实际全部位于 上。从上述结果来看，哪怕有人能够证明，存在常数 使得 上面没有黎曼函数的零点，都是一个重大的突破。而一般来说，一次到位的结果通常来说都是错误的。

总结

黎曼猜想之所以如此难解，根本原因在于它所牵涉的是素数分布的深层结构与复变函数的微妙行为之间的桥梁。这个猜想声称，黎曼函数所有非平凡零点的实部都是 1/2，而这一点虽看似单纯，却隐藏着极其复杂的解析结构。黎曼函数是一个在整个复平面上解析的函数，其行为受到极高阶、非线性、全局变量的共同影响——它不是一个简单的代数对象，而是一种高度刚性的全纯函数。更深层的困难在于，黎曼函数的零点并非孤立的“点”，而是牵动整个数论体系：它们决定着素数的统计规律与误差幅度。任何企图“看清”这些零点位置的工具，都必须同时具备解析、代数、几何乃至随机性理论的深度，而当前数学尚未发展出足以全面穿透这一层层屏障的统一语言。因此，黎曼猜想的难度不仅在于其技术复杂性，更在于它位于数学多个分支交汇的边界地带，是一道真正横跨整个数学版图的深渊。

素数的呼吸：咫尺天涯与辽阔星河

在数字的汪洋中，素数如同散落的星辰，它们孤独地存在，除了自身和1，不被任何其他整数整除。它们的分布，是数学中最古老也最迷人的谜题之一。欧几里得早已证明，这星辰之河奔流不息，永无止境。然而，星辰之间的距离，却并非均匀。它们时而亲密依偎，时而相隔万里，仿佛宇宙本身在无声地呼吸。

为了证明素数有无穷多个，这里举两个常见的证明方法。

1. 欧几里得证明（反证法，公元前300年）

• 思路：假设素数有限，构造一个新数导出矛盾。
• 步骤：
  1. 假设素数只有有限个，记为 。
  2. 构造新数 。
  3. 不被任何 整除（因 )。
  4. 因此 是素数或含有新素因子，与假设矛盾。
• 意义：最古老且简洁的证明，开创了反证法的经典应用。

2. 欧拉证明（分析学方法，18世纪）

• 思路：利用调和级数发散和算术基本定理。
• 步骤：
  1. 对调和级数取对数：
  2. 由调和级数发散 → 右端求和发散 → 素数个数无限。
• 关键公式：
• 意义：首次将分析与数论结合，启发了黎曼 函数研究。

两个证明不仅确认了素数的无限性，更推动了数论和分析发展，体现了数学的多样性与统一性。

素数定理（Prime Number Theorem, PNT）是数论中描述素数分布渐进行为的核心定理，其揭示了素数在自然数中的密度规律。设 表示不超过实数 的素数个数，则当 时，有： ，其中符号 表示渐近等价，即： 。通过数值的计算，我们可以直接得到下面的计算结果。

除此之外，素数定理还有以下等价表述，均描述相同的渐近行为：

对数积分形式（更精确）：

，其中 是对数积分函数，满足 。

切比雪夫函数形式：

定义 （对所有素数 的 求和），则： 。定义 （其中 是冯·曼戈尔特函数，当 时 ，否则为 0），则：

素数定理的直观解释。素数定理表明，当 极大时， 附近的素数密度约为 。示例：

当 时，，而 ，比值约 。

当 时，，，比值约 ，更接近 $ latex 1$。

素数定理的历史意义：高斯（1792年）和勒让德（1798年）通过数值计算猜想 。切比雪夫（1852年）证明 的极限若存在必为 ，并给出上下界

。

阿达玛与德·拉·瓦莱·普桑（1896年）独立利用复分析（黎曼ζ函数非零区域）完成证明。塞尔伯格与埃尔德什（1949年）给出仅用实分析的初等证明。

素数定理与黎曼猜想的关系：素数定理等价于黎曼 函数在 上无非平凡零点。黎曼猜想若成立，可将误差项优化为 。狄利克雷定理（算术级数中的素数分布）是素数定理在模 余 （）素数集上的推广。

素数定理以简洁公式 揭示了素数的宏观分布规律，成为解析数论的基石，其证明融合了复分析与深刻数论思想，影响深远。

咫尺之间：孪生之梦

最令人心动的亲密，莫过于“孪生素数”——像（3,5）、（11,13）、（17,19）这样，仅相差2的素数对。它们如同双生子，在数轴上紧紧相随。孪生素数猜想断言：这样的“双生子”有无穷多对。它直观得近乎理所当然，却让最聪慧的头脑困扰了数百年。

长久以来，数学家们只能步步逼近。假设 表示第 n 个素数，那么相邻素数的间距就是 。当 是正整数的时候，定义 ，那么 就是孪生素数猜想。

从历史发展的历程来看，数学家A. de Polignac提出猜想：对于任意偶数 ，存在无穷多对相邻素数，其差恰好为 。这为后续研究提供了方向，后续称之为1849年 Polignac猜想。

在1919年，挪威数学家V. Brun证明孪生素数倒数和收敛（Brun常数），并开创现代筛法。孪生素数的倒数和是数论中关于素数分布的一个重要结论。该结论揭示了孪生素数（即相差 2 的素数对，如 (3,5)、(11,13)）的分布特征，其核心内容如下：

设 为所有孪生素数对 的集合，则其倒数和收敛： 该级数的极限值称为 布鲁恩常数（Brun’s constant），记为 ： 。

孪生素数的倒数和与素数倒数和对比：所有素数的倒数和发散（即 ），而孪生素数的倒数和收敛。这表明孪生素数比全体素数稀疏得多，即使孪生素数有无穷多对（孪生素数猜想尚未证明），其分布密度也足够低以保证倒数和有限。收敛性说明孪生素数的分布满足： ， 即孪生素数的数量增长慢于 （对比素数定理 ）。

布鲁恩的证明基于改进的筛法理论，核心步骤如下：

1. 筛法构造：定义集合 S(x) 为所有不大于 x 的正整数 n 所组成的集合，这些 n 满足的条件是：对于所有小于 的素数 p，p 既不整除 n，也不整除 n+2。则 。
2. 上界估计：布鲁恩通过组合计数证明： ，其中 C为常数，具体推导利用容斥原理和不等式放缩（如切比雪夫边界）。
3. 倒数和收敛：由 可得：

对前 个孪生素数对计算部分和： 例如：当 时，；当 时，。针对收敛速度这个问题，因 （ 为孪生素数常数），级数收敛极慢，需极大 才能接近 。

布鲁恩定理以简洁而深刻的结论揭示了孪生素数分布的稀疏性，其证明融合了筛法与组合数学的精妙思想，成为解析数论的里程碑之一。该结论不仅推动了素数分布理论的进展，也在计算科学中留下有趣印记。

除此之外，布鲁恩还首次证明存在无穷多对9-殆素数（9-almost primes）的差为2（即“9+9”）。在1947年匈牙利数学家A. Rényi证明：存在常数 ，使得有无穷多对素数 和 -殆素数 ，其差为2（即“k+1”）。在1966年，E. Bombieri与H. Davenport证明孪生素数密度上界：，表明孪生素数分布稀疏，后人称之为Bombieri-Davenport上界。在1978年，中国数学家陈景润证明：存在无穷多对素数 和2-殆素数 ，其差为2（即“1+2”），将筛法推向顶峰。在2005年，D. Goldston、J. Pintz和C. Yildirim证明：两个素数之间的间隙相比平均值可任意小。在强猜想假设（GEH）下，存在无穷多对素数差不超过16。

一个关键的突破来自张益唐教授。2013年，这位沉寂多年的学者带来震撼：存在无穷多对素数，它们的距离小于一个固定的数字——7000万。这个数字看似庞大，在无限的尺度下却微不足道。它如同在黑暗中凿开一道缝隙，证明素数并非总是疏离。在2013年4月，张益唐在《数学年刊》发表《素数间的有界间隔》，英文名是《Bounded Gaps between Primes》。首次严格证明：存在无穷多对素数对 ，其差不超过7000万（即 ）。这一成果解决了弱哥德巴赫猜想的关键部分。

随后，数学界的“接力赛”开启，陶哲轩领导的“博学者计划”和其他数学家（如詹姆斯·梅纳德）不断优化工具，将这个距离极限压缩到了令人惊叹的246。我们离证明孪生素数猜想（距离为2）依然遥远，但曙光已现。这咫尺之遥的探索，揭示了素数分布中深藏的、难以捉摸的规律性。在 2013年5–6月，常数优化热潮开启，张益唐的成果引发全球数学家合作优化常数：

• 5月28日：降至6000万
• 5月31日：降至4200万
• 6月2日：降至1300万
• 6月5日：降至40万
• 2013年底：Polymath项目结合James Maynard新方法，将常数降至246。

到了2013年11月，James Maynard 在素数有界间距上取得了独立突破。James Maynard独立提出更简方法，将素数差常数降至600，并证明：对任意 ，存在常数 ，使得无穷多对素数差不超过 （Polymath项目进一步优化至246）。

2015年至今：后续进展Polymath8b项目给出精细上界公式：，并探索广义孪生素数分布。

素数小间距的关键结论如下：

• 核心问题：素数间距能否无限小？孪生素数猜想（差为2）是否成立？
• 核心工具：筛法（Brun–Selberg）、指数和（Goldston–Pintz–Yildirim）、张益唐的松弛筛法结合Bombieri–Vinogradov定理。
• 未解难题：孪生素数猜想（）仍未完全证明，但246已是迄今最佳上界。

辽阔星河：自由的旷野

然而，素数的呼吸并非只有浅吟低唱。它们也渴望辽阔的空间。你能想象在数轴上找到任意长的、完全没有素数的“荒漠”吗？答案是肯定的。

一个巧妙的构造揭示了这种自由：考虑一串连续的数字：n! + 2, n! + 3, n! + 4, …, n! + n。对于任意大于1的整数k（k ≤ n），n! + k 都能被k整除（因为n!包含k）。因此，这串长达n-1个连续数字中，没有一个是素数！随着n的增大，这片“荒漠”可以任意延长。这意味着，素数之间的间隔，可以像宇宙膨胀一样，变得无比巨大。

数学家们不满足于此，他们想知道这间隔到底能有多大。埃尔德什等数学家用更精密的工具证明：在小于某个巨大数字X的范围内，必然存在相邻素数，其间隔远大于它们的“平均间隔”（约为ln X）。具体来说，这个最大间隔至少可以像 (ln X * ln ln X * ln ln ln ln X) / (ln ln ln X) 那样增长（尽管公式复杂，它描绘了一种远超平均的、爆发式的增长）。这如同在星辰之河中，存在着难以想象的辽阔寂静地带。

素数大间距（Big Gaps）研究素数间隔的渐进增长，其难度不亚于素数的小间距。在1931年，Westzynthius的开创性工作结果证明存在无穷多个素数间隔大于 ，即：

。

首次确立素数间隔可无限超越对数尺度。

在1935年，Erdős将上述结果进行改进。他引入新方法，证明：

。

Erdős首次在分母中引入三重对数项，显著提升下界。

在1938年：Rankin的又取得了重大突破。优化常数并引入四重对数项：

。

证明下界常数可大于 （后经Pintz等优化至 ）。其结果长期未被超越，成为经典基准。

到了2014年：Ford–Green–Konyagin–Tao–Maynard的革命性进展，彻底改进渐进阶：

。

首次将分母降为 ，突破Rankin框架。

截至2024年，相邻素数的最大间距是：（对应素数 ）。上述渐进结果保证了间隔的无限增长，但具体数值依赖计算验证。素数大间距的发展历程体现了从初等证明到调和分析、组合数学的深度融合，尤其是2014年工作融合了多重数学工具，重塑了素数间隔的理论框架。

宇宙的韵律

素数的间距，就这样在“亲密无间”与“天各一方”之间摆荡。小间距（如孪生猜想）体现了素数分布潜在的某种“粘性”或聚集倾向；而大间距的存在，则彰显了其固有的、不可预测的随机性和自由。

数学家	核心贡献
Green & Tao	素数中存在任意长等差数列（Green-Tao 定理）。
张益唐	素数间隙有界，开启小间隙研究。
Maynard	独立优化间隙至 600；推广至多素数聚类；筛法创新。
Ford–Green–Konyagin–Tao–Maynard	证明素数间隙可任意大（解决 Erdős–Rankin 猜想）。
Polymath	协作优化间隙至 246，推动开放式数学研究。

这些成果共同推动了解析数论的突破，揭示了素数分布的深层结构，并为后续研究（如孪生素数猜想）奠定了基础。理解这些间距，就是试图破译宇宙在整数序列中留下的密码。张益唐的7000万、梅纳德的筛法革新、构造出的任意长荒漠、以及关于最大间隔的精密估计，都是人类智慧在探索这深邃韵律时留下的足迹。它们告诉我们，即使在最基础的数字序列里，也蕴藏着无限的惊奇——既有令人心安的亲密可能，也有挑战想象的辽阔自由。素数的呼吸，是数学宇宙永恒而迷人的心跳。

在现代数学的研究中，数学教育（Math Education）作为一个重要的研究领域，虽然看似不如一些前沿方向那么引人注目，但它仍然在 ICM 的标准中占有一席之地，数学教育也算是数学的研究方向之一。随着人工智能（AI）技术的飞速发展，数学教育与 AI 的结合呈现出巨大的潜力。从小学到大学的整个教育体系，AI 技术可以提供个性化的教学体验，助力每一个学生提升其数学能力。

如果是 AI 与数学教育相结合，那么可以做的东西就太多了。从小学开始，到中学，一直到后面的大学教育，都有数学的身影。从小学到大学阶段，AI 都能够提供个性化的教学体验。例如，在基础教育阶段，AI 可以通过智能算法分析学生的学习行为和学习进度，提供定制化的学习内容，帮助学生发现自己的薄弱环节，进而进行针对性训练。这种方式相比传统的一刀切式教学，可以更有效地提升学生的数学素养和解决问题的能力。

对于中学和大学阶段，AI 能够借助个性化推荐，挖掘学生在学习数学过程中可能遇到的概念理解偏差，帮助老师实时调整教学方法。同时，通过智能评测，AI 可以实时监控学生的学习进度，及时进行干预或提供更多的学习资源，甚至帮助学生进行模拟题训练和成绩预测。AI 还可以在数学教育的教学内容开发和教育评估中扮演重要角色。它不仅能协助教师设计更加丰富和互动性的课程内容，还能提供精准的学习成果评估，帮助教育者不断调整教学策略，实现精准化教育。

在中学阶段，借助学生每个人自己的错题，每个学生都可以实现基于错题的一个AI习题知识库，无论是放在“知乎直答”还是 ima.copilot 这个工具中，都可以实现这样的效果。学生只需要把自己的错题记录下来，然后上传系统，每隔一段时间就进行错题回顾，于是就可以实现错题的重复练习，达到进一步地提升效果。

在大学阶段，数学学习不仅限于基础知识的掌握，还涉及大量的专业文献和研究论文的阅读与分析。面对复杂的数学论文，传统的阅读方式往往需要耗费大量的时间与精力，尤其是在理解深奥的理论、推导过程或未解决的问题时，学生和研究者往往感到力不从心。然而，借助 AI 工具，读者可以更高效地进行论文的“粗读”和初步分析。

通过 AI 工具的支持，学生可以先对整篇论文进行快速扫描和概括，AI 可以提取出文章的核心内容，包括主要结论、方法论以及重要的数学定理和公式。这种自动化的初步整理，帮助学生更快速地把握论文的大致框架，从而为更深入的研究提供指引。此外，AI 工具还能够根据学生的需求，进行论文内容的梳理和重构，帮助他们在特定的学术背景或研究领域中找到所需的信息。这对于那些内容繁杂、篇幅冗长的论文尤其重要，能有效节省时间，减少信息过载的困扰。

更重要的是，AI 工具能够自动识别论文中的未解决问题和猜想，帮助学生发现当前研究领域的空白和潜在的研究方向。例如，AI 可以通过分析现有文献的结论和讨论，识别出研究中的不足和未解之谜，甚至根据现有的数学理论预测一些尚未得到验证的猜想。这种功能不仅对学生的学习有益，也为研究者提供了创新的灵感和研究的潜在方向。

整体来看，AI 与数学教育的结合是一个巨大的潜力领域，不仅可以提升学生的数学能力，也能推动教育行业的全面升级。从这种角度来看，数学教育作为一个研究方向，不仅符合 ICM 的标准，也是推动数学和教育现代化的重要领域。