天衣岂无缝，匠心剪接成。

浑然归一体，广邃妙绝伦。

造化爱几何，四力纤维能。

千古存心事，欧高黎嘉陈。

这首诗是1975年杨振宁写给陈省身的。最后一句“欧高黎嘉陈”中，杨振宁把陈省身和数学史上的欧几里得、高斯、黎曼和嘉当并列，称他为数学史几何学上的第五人。而高斯、黎曼均属于 18 世纪的德国数学家，在数学史上有着不可磨灭的贡献。

德国的数学史

德国的数学发展历史悠久且贡献卓著，尤其在近代和现代数学中占据核心地位。17世纪，戈特弗里德·威廉·莱布尼茨（Gottfried Wilhelm Leibniz）独立发明了微积分（与牛顿同时期），并发展了二进制系统，对数学分析、逻辑学和计算理论影响深远。18至19世纪，卡尔·弗里德里希·高斯（Carl Friedrich Gauss）在数论、代数、几何和分析等领域做出奠基性工作，如证明代数基本定理、发展非欧几何理论（与波尔约和罗巴切夫斯基并列）以及最小二乘法。19世纪下半叶，乔治·康托尔（Georg Cantor）创立集合论，引入无穷集合和超穷数概念，彻底改变了数学的基础。大卫·希尔伯特（David Hilbert）在20世纪初提出23个数学问题，推动了现代数学多个分支的发展，并在公理化体系和数学基础领域贡献显著。哥廷根学派成为全球数学研究中心，培养了埃米·诺特（Emmy Noether）等杰出学者，其抽象代数和守恒定理工作影响深远。德国数学以严谨性、抽象性和理论深度著称，为全球数学教育、研究及应用奠定了坚实基础。

16世纪前的德国数学

17世纪以前的德国数学发展虽不如同时期的意大利或法国那样耀眼，但仍有一批重要数学家为欧洲数学的复兴与传播做出了贡献。其中，雷格蒙塔努斯（Regiomontanus，1436–1476） 是文艺复兴时期的关键人物。他本名约翰内斯·米勒（Johannes Müller），因出生于柯尼斯堡（Königsberg）而取拉丁化别名“雷格蒙塔努斯”。他系统翻译并注释了希腊数学著作，尤其是托勒密的《天球论》和阿波罗尼奥斯的《圆锥曲线论》，推动了三角学的独立发展。他撰写的《论各种三角形》（De triangulis omnimodis）是欧洲第一部系统的三角学专著，首次明确将三角学作为独立学科而非天文学附庸，并改进了正弦表的计算精度，为后世导航和天文计算提供了基础工具。

16世纪的克里斯托夫·鲁道夫（Christoph Rudolf，1499–1545） 在代数学领域有所建树。他的代表作《代数术》（Coss）系统介绍了代数符号和方程求解方法，推动了德国代数学的普及。书中首次使用根号符号（√）表示平方根，这一符号后来被广泛采纳并沿用至今。同时，米夏埃尔·斯蒂费尔（Michael Stifel，1487–1567） 进一步发展了代数和数论。他在《整数算术》（Arithmetica integra）中研究了二项式系数、算术序列及无理数理论，并尝试用几何方法证明代数命题，为符号代数的形成奠定了基础。斯蒂费尔还曾与马丁·路德合作，将数学思想应用于宗教改革时期的文献研究。

亚当·里斯（Adam Riese，1492–1559） 虽非理论数学家，却以实用算术教育影响了德国数学普及。他编写的算术教科书《计算艺术》（Rechenkunst）推广了印度-阿拉伯数字计算法，取代了传统的算盘计算，成为商人和学生的重要工具书，被誉为“德国计算大师”。这一时期德国数学的特点是从实用算术向理论学科过渡，并为17世纪莱布尼茨等人的重大突破奠定了基础。

17世纪的德国数学

17世纪是德国数学发展的重要时期，涌现出多位杰出数学家，为现代数学奠定了基础。戈特弗里德·威廉·莱布尼茨（Gottfried Wilhelm Leibniz）是这一时期最著名的代表人物，他独立于牛顿发明了微积分，并发展了二进制系统，对数学和哲学产生了深远影响。莱布尼茨在符号表示方面做出了重要贡献，引入了积分符号∫和微分符号d，这些符号至今仍在广泛使用。他还研究了无穷级数、微分方程和组合数学，为后续数学发展提供了重要工具。莱布尼茨提出了符号逻辑的初步思想，这些贡献对后世数学和计算机科学产生了深远影响。他的工作尤其注重符号化与形式化，为现代数学语言奠定了基础。

另一位重要数学家是约翰内斯·开普勒（Johannes Kepler），虽然他主要活跃于16世纪末至17世纪初，但其工作对17世纪数学发展具有持续影响。开普勒提出了行星运动三大定律，这些定律不仅推动了天文学发展，还促进了数学中圆锥曲线和积分思想的应用。他在《葡萄酒桶的立体几何》中研究了旋转体的体积计算，为微积分的诞生提供了前期准备。

克里斯托夫·克拉维乌斯（Christoph Clavius）也是17世纪初期德国数学的重要人物，他主要贡献在于历法改革和数学教育。克拉维乌斯参与了格里高利历的制定，并在其数学著作中系统整理了欧几里得几何学，推动了数学在德国的传播和教育规范化。

18世纪的德国数学

德国数学在17世纪的表现，体现了从文艺复兴到科学革命的过渡特征，强调数学与自然科学的紧密结合，为18世纪数学的蓬勃发展奠定了坚实基础，18世纪德国数学的发展涌现了多位杰出人物。

莱布尼茨的学生克里斯蒂安·冯·沃尔夫（Christian von Wolff）在推广莱布尼茨的数学和哲学思想方面发挥了重要作用，他通过系统化的教材和著作，使这些理论在德语世界得到广泛传播，促进了数学教育的发展。

约翰·海因里希·朗伯（Johann Heinrich Lambert）也在该时期贡献显著，他证明了π是无理数，并在双曲函数和非欧几何的早期探索中取得了进展，为19世纪数学的革命性发展埋下了伏笔。

总体而言，18世纪德国数学以莱布尼茨的符号化方法和欧拉的分析学成就为核心，融合了理论创新与教育推广，为现代数学的体系化奠定了坚实基础。

19世纪的德国数学

卡尔·弗里德里希·高斯

19世纪的德国数学界涌现了众多杰出数学家，他们的贡献奠定了现代数学的基石。卡尔·弗里德里希·高斯（Carl Friedrich Gauss，1777–1855） 被誉为“数学王子”，他在数论、代数、分析和几何等多个领域均有深远影响。高斯提出了正态分布理论，发展了最小二乘法，并发表了《算术研究》，系统阐述了模运算和二次互反律，为现代数论奠定了基础。此外，他在非欧几何领域的研究虽未及时公开，但后来被证实对几何学发展具有革命性意义。他的贡献几乎遍及所有数学分支，并在物理学、天文学和大地测量学等领域有深远影响。

数论领域的奠基性工作：

高斯在1801年出版的《算术研究》（Disquisitiones Arithmeticae）中系统性地构建了现代数论的基础。他引入了同余理论（符号“≡”至今仍被使用），深入研究了二次剩余、二次互反律（并给出了第一个严格证明），并提出了高斯整数（复整数）的概念，推动了代数数论的发展。他还证明了费马多边形数定理，并对素数分布提出了猜想（后来成为素数定理）。

代数与方程论：

高斯在代数学中的核心贡献是证明了代数基本定理（每个复系数多项式都有至少一个复根），并给出了多种证明方法。他还研究了分圆方程（cyclotomic equations），即形如 xn=1x^n = 1xn=1
的方程，其工作为伽罗瓦理论的出现奠定了基础。在文档中提到的“高斯的解决分圆方程的工作”正是指他在这一领域的研究。

几何学的革新：

高斯是非欧几何的早期探索者之一（尽管未公开发表），他提出了内蕴几何的概念，发展了曲面理论（如高斯曲率），并建立了微分几何的基础。他的工作直接影响了几何学的现代化进程。

分析学与数学物理：

高斯在分析学中贡献了高斯积分（正态分布相关的积分）、超几何级数研究，以及数值计算方法（如高斯消元法、高斯-赛德尔迭代）。他还与威廉·韦伯合作研究了电磁学，提出了高斯单位制，并发表了电磁学中的高斯定律。

天文学与大地测量学：

高斯发展了行星轨道计算的最小二乘法（用于预测谷神星的位置），并提出了高斯分布（正态分布），这一分布在概率论和统计学中成为核心工具。在大地测量学中，他研究了曲面的映射问题，提出了高斯投影法。

高斯的数学思想以严谨、深刻和前瞻性著称，他的许多工作（如非欧几何）在当时未被完全理解，但后来成为现代数学的基石。他追求完美，主张“少而精”，其著作和笔记至今仍在激励数学家探索未知领域。

伯恩哈德·黎曼

伯恩哈德·黎曼（Bernhard Riemann，1826－1866） 以其对几何和分析的贡献闻名。他引入了黎曼几何，通过黎曼曲面的概念复分析推向新高度，并提出了黎曼积分和黎曼猜想，后者至今仍是数论中未解决的核心问题。他的工作为爱因斯坦的广义相对论提供了数学工具。他的工作在数学和物理学多个领域产生了深远的影响。黎曼出生于汉诺威王国的一个贫困牧师家庭，早年显示出非凡的数学天赋，在哥廷根大学和柏林大学学习期间受到高斯、狄利克雷等数学巨匠的指导。他的学术生涯虽短暂，却奠定了现代数学中多个重要分支的基础。

黎曼最著名的贡献之一是黎曼几何，他在1854年的就职演讲《论几何学基础中的假设》中提出了弯曲空间中的几何概念，推广了欧几里得几何学。他引入的黎曼度量和曲率张量为后来爱因斯坦的广义相对论提供了数学框架，彻底改变了人们对空间、时间和引力的理解。黎曼几何不仅成为微分几何的核心，也在现代理论物理中具有不可替代的地位。

在复分析领域，黎曼提出了黎曼曲面的概念，将复变函数的研究从平面推广到多值函数和复杂拓扑结构上。他著名的黎映射定理（黎曼映射定理）表明任何单连通开集（非全平面）都可以共形映射到单位圆盘，这一结果在几何函数论中具有根本重要性。此外，黎曼在椭圆函数和阿贝尔函数方面也有深刻的工作。

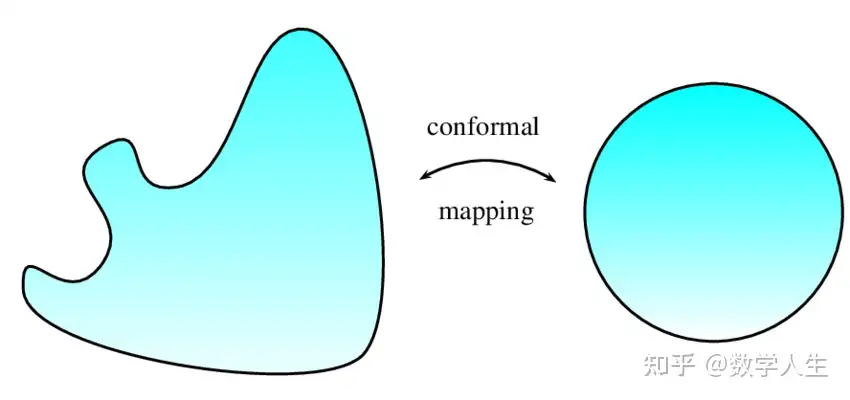
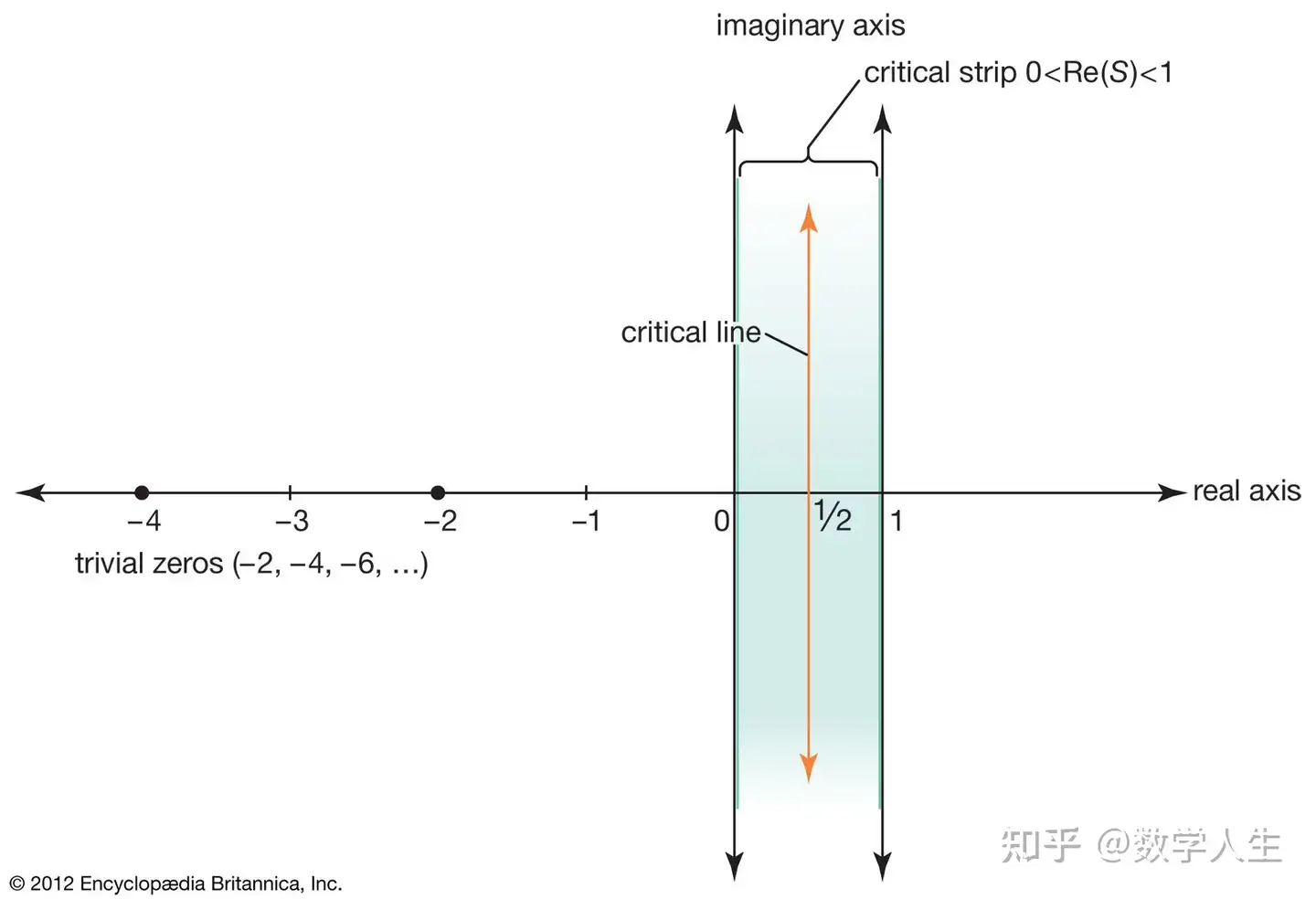
数论中，黎曼在1859年的论文《论小于给定数值的素数个数》中引入了黎曼ζ函数，并提出了著名的黎曼猜想（Riemann Hypothesis），即ζ函数的所有非平凡零点的实部均为1/2。这一猜想至今仍是数学中未解决的最重要问题之一，其证明将极大地推动素数分布理论的发展。

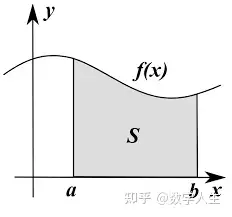
黎曼还对积分理论做出了革新，提出了黎曼积分的定义，为后来勒贝格积分和其他更一般的积分理论奠定了基础。在实分析中，他研究了傅里叶级数的收敛性问题，并给出了黎曼可积性的条件。

在数学物理方面，黎曼研究了声波传播、流体动力学和电磁学等问题，他关于冲击波的工作为偏微分方程理论提供了新工具。他提出的黎曼问题在双曲型守恒律中仍是研究的热点。黎曼的思想极具前瞻性和深度，他的工作不仅推动了纯数学的发展，也为现代物理学提供了关键工具。尽管他生命短暂（仅享年39岁），但其贡献跨越了几何、分析、数论和物理等多个领域，使他成为19世纪最伟大的数学家之一。

利奥波德·克罗内克（Leopold Kronecker，1823 – 1891） 是代数和数论的重要人物，他主张“上帝创造了整数，其余皆是人的工作”，强调数学应基于整数构建。他发展了代数数论，提出了克罗内克乘积和克罗内克极限公式，并对代数学的结构性研究有深远影响。

卡尔·魏尔斯特拉斯（Karl Weierstrass，1851-1897） 被誉为“现代分析之父”，他严格化了极限、连续和微积分的定义，提出了ε-δ语言，消除了早期分析中的不严谨性。他还研究了椭圆函数和变分法，其工作为实分析和复分析提供了坚实基础。

费迪南德·戈特霍尔德·艾森斯坦（Ferdinand Gotthold Eisenstein，1823-1852） 虽英年早逝，但在数论和代数领域贡献显著。他研究了二次形式、立方互反律和椭圆函数，艾森斯坦级数和艾森stein不可约准则至今是重要工具。

菲利克斯·克莱因（Felix Klein，1849-1925） 以埃尔兰根纲领闻名，该纲领通过群论统一了几何学分类。他还研究了复变函数、非欧几何和数学教育，推动了几何与群论的结合，对现代数学发展有深远影响。

格奥尔格·康托尔（Georg Cantor，1845–1918）是德国数学家，集合论的创始人，对现代数学产生了深远影响。他出生于俄罗斯圣彼得堡，后移居德国，在哈勒大学度过学术生涯。康托尔首次系统提出了无穷集合的理论，证明了无穷集合存在不同大小，例如实数集比自然数集“更大”，并引入了基数与序数的概念。他的对角线论证法成为逻辑与计算机科学的重要基础。尽管其理论初期遭到克罗内克等数学家的强烈反对，甚至引发哲学与神学争议，康托尔始终坚信自己的思想是“上帝传达的真理”。晚年他饱受抑郁症困扰，但其工作最终被希尔伯特等学者推崇，为数学奠定了新的基石。1904年，他荣获英国皇家学会的西尔维斯特奖章。

这些数学家的集体工作使德国成为19世纪数学研究的中心，他们的理论不仅推动了纯数学的发展，还为物理学、工程学等领域提供了关键工具。

20世纪的德国数学

大卫·希尔伯特

20世纪德国数学在世界数学史上占据重要地位，涌现出一批影响深远的数学家。大卫·希尔伯特（David Hilbert，1862–1943）是这一时期的杰出代表，他在1900年国际数学家大会上提出了23个数学问题，为20世纪的数学研究指明了方向，对数学基础、数论、代数几何和数学物理等领域产生了深远影响。希尔伯特在公理化方法和数学基础方面的贡献尤为突出，他提出的“希尔伯特计划”试图为数学建立坚实的形式化基础。

希尔伯特早期的重要贡献集中在不变量理论领域。他证明了不变量的有限基定理，表明任何不变量的系统总可以由有限个不变量生成，这一结果解决了哥尔丹问题，并引入了非构造性证明方法，为现代抽象代数奠定了基础。随后，他将注意力转向数论，在1897年的《数论报告》中系统总结了代数数论的成果，并提出希尔伯特类域论等关键问题，推动了20世纪数论的深远发展。

在几何学领域，希尔伯特于1899年发表《几何基础》，首次以严格公理化的方式重构欧几里得几何。他提出一组完备且独立的公理系统，并深入探讨了公理系统的相容性、独立性和完备性，这一工作不仅革新了几何学的基础，更促进了数学公理化思想的普及，对后续数学研究产生了范式性影响。

20世纪20年代，希尔伯特转向数学基础研究，提出“希尔伯特纲领”，旨在通过有限主义方法证明数学系统的相容性，以应对集合论悖论带来的危机。尽管哥德尔的不完备定理表明这一纲领无法完全实现，但希尔伯特的形式化方法催生了证明论这一新领域，并深刻影响了现代逻辑和计算机科学的发展。

希尔伯特在积分方程和数学物理领域也有杰出贡献。他发展了希尔伯特空间理论，为泛函分析奠定了基础，这一概念后来成为量子力学的重要数学框架。他与弟子合作的研究还推动了变分法、特征值理论等领域的进展。希尔伯特的学术遗产不仅体现在具体定理和理论上，更在于他高瞻远瞩的问题意识、对数学统一性的追求以及培养大批杰出学生的教育贡献，使他成为当之无愧的现代数学奠基者之一。

埃米·诺特（Emmy Noether，1882-1935）是抽象代数的奠基人之一，她的诺特定理将对称性与守恒定律联系起来，对理论物理学的发展起到了关键作用。她在环论、域论和模论等领域的开创性工作为现代代数结构研究奠定了基石。赫尔曼·外尔（Hermann Weyl）在群论、表示论和数学物理等领域贡献卓著，他的工作涉及连续群、量子力学和广义相对论，尤其在对称性和规范场理论方面有深远影响。

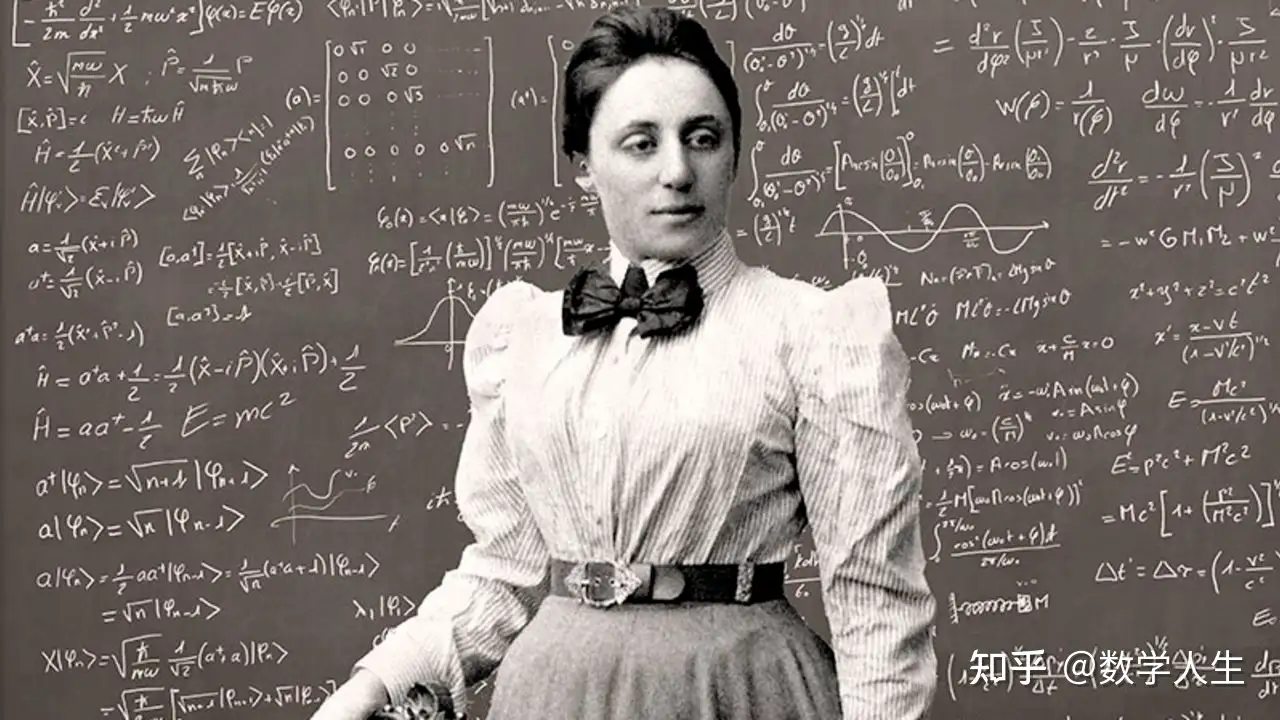
菲利克斯·豪斯多夫（Felix Hausdorff，1868-1942）是点集拓扑学的创始人之一，他提出的豪斯多夫空间和豪斯多夫维数等概念成为现代拓扑学和分形几何的基础。格奥尔格·康托尔（Georg Cantor）虽然主要工作在19世纪末，但他的集合论和超穷数理论在20世纪被广泛接受并进一步发展，对数学基础和逻辑学产生了革命性影响。此外，卡尔·西格尔（Carl Siegel）在数论和多复变函数论方面的工作，以及赫尔曼·闵可夫斯基（Hermann Minkowski）在数论和相对论中的几何方法，也为20世纪数学的发展做出了重要贡献。

这些德国数学家的成就不仅推动了纯粹数学的进步，还在理论物理学、计算机科学和工程学等领域产生了广泛的应用，奠定了现代数学的许多核心分支的基础。

简单介绍

斯里尼瓦瑟·拉马努金（1887–1920）是印度数学史上一位传奇式的天才人物。他出身贫寒，未接受过正规高等教育，却凭借超凡的直觉和自学能力，在数论、无穷级数、连分数和分拆函数等领域做出了深远而独创的贡献。在孤立的研究环境中，他独立发现了大量定理，其中许多结果甚至重现并超越了欧洲数学家的成果。1913年，他致信英国数学家G.H.哈代，其才华得到赏识，随后赴剑桥大学合作研究，成为英国皇家学会会员和三一学院研究员。尽管英年早逝，他留下的数千个公式和猜想为现代数学研究提供了丰富的源泉，被公认为数学巨匠。

在印度的生活

一、神童的诞生与早期教育（1887-1904）

拉马努金于1887年12月22日出生于印度泰米尔纳德邦的埃罗德（Erode），在一个贫困的婆罗门家庭中长大。他的父亲是纱丽店的一名职员，母亲是家庭主妇，也在当地寺庙演唱宗教歌曲。童年时期，他接受了深厚的婆罗门文化熏陶，学习宗教歌曲和传统仪式。他的数学天赋在幼年便已显现。1897年，10岁的拉马努金以优异成绩通过初级考试，在英语、泰米尔语、地理和算术科目中名列学区第一。同年，他进入贡伯戈纳姆市高中（Town Higher Secondary School），首次接触正规数学教育。11岁时，他已经掌握了家中两位大学生房客的全部数学知识。13岁时，他完全自学掌握了S.L. Loney的《三角学》高级教材，并独立发现了复杂定理。14岁时，他开始获得学校颁发的优异证书和学术奖项，并协助学校完成1200名学生与35名教师的复杂分配工作，能在规定时间一半内完成数学考试，并熟练运用几何和无穷级数。

二、坎坷的大学之路与独立研究（1904-1909）

1904年，拉马努金从市高中毕业，校长克里希纳斯瓦米·艾耶（Krishnaswami Iyer）授予他K. Ranganatha Rao数学奖，并称他是一位“应得分数超过满分”的杰出学生。他凭借此成绩获得政府文理学院（Government Arts College, Kumbakonam）的奖学金。然而，悲剧也随之而来。他对数学的痴迷导致他完全忽视了其他学科。1905年，他因非数学课程不及格而失去了奖学金。他后来进入马德拉斯的帕夏帕学院（Pachaiyappa’s College），再次在数学上表现出色，但在生理学等科目上成绩糟糕。1906年12月，他未能通过文学学士学位考试，一年后再试依旧失败。没有学位，他被迫离开大学，陷入了极端贫困，甚至时常遭受饥饿的折磨。在此期间，他完全依靠自学进行独立的数学研究。没有指导、没有同行交流，他在孤立无援的环境中持续探索。他通过做家教赚取微薄收入，但常常食不果腹。他的家人，尽管经济拮据，却始终包容他，没有强迫他放弃数学去寻找一份常规工作。

三、转折点：被学术界发现（1910-1913）

在贫困交加中，拉马努金的转机终于出现。他开始在《印度数学会刊》（Journal of the Indian Mathematical Society）上提出并解决问题。1911年，他在该期刊上发表了一篇关于伯努利数的杰出研究论文，这使他在马德拉斯地区开始声名鹊起，被誉为“数学天才”。1912-1913年间，在朋友和导师的鼓励下，他决定将自己的研究成果寄给英国剑桥的数学家。他写信给三位学者，其中最重要的一封是1913年1月16日写给G.H.哈代（G.H. Hardy）的信。随信附上了一份长达11页的清单，列出了120个他独立发现的定理和公式，其中许多涉及连分数、无穷级数和素数分布等领域。这封信改变了历史。哈代最初对这位“无名印度职员”的手稿持怀疑态度，但很快就被其中一些结果的深度和美感所震撼。他与同事J.E.李特尔伍德（J.E. Littlewood）仔细研究后，确信拉马努金是一位“与欧拉和高斯同等级别的天才”。哈代回信邀请他来剑桥合作。

四、赴英前的准备与本土荣誉

拉马努金最初因宗教原因（远洋旅行会失去种姓身份）和母亲的反对于1913年拒绝了哈代的邀请。然而，随着与哈代的通信持续，他的才华引起了马德拉斯大学的高度重视。1913年5月，在马德拉斯大学数学教授E.W. Middlemast（他写道：“我强烈推荐这位申请者。他是一个在数学，尤其是数论方面具有非凡能力的年轻人。”）的极力举荐下，大学决定破例授予拉马努金一份为期两年的特殊研究奖学金，使他能够辞去港务局的职员工作，全身心投入数学研究。最终，在各方努力和母亲的妥协下，拉马努金接受了哈代的第二次邀请。1914年3月17日，他从印度启航前往英国，结束了他在印度孤独而辉煌的探索时期，开启了他与世界数学中心碰撞的新篇章。

与哈代的合作及剑桥时期

尽管哈代已为他在剑桥三一学院争取到了为期两年的奖学金，拉马努金启程前却充满了挣扎。作为一名正统的婆罗门，他极度担忧这次远行会让他失去种姓身份，并且对英国的寒冷气候与饮食禁忌感到恐惧。最终，在印度几位数学教授的极力劝说下，他才终于成行。经过四周的海上航行，其中三天他因晕船而备受折磨，他于4月14日抵达伦敦。哈代的同事E.H.内维尔（E. H. Neville）开着一辆汽车在码头等候他，四天后，便将他带到了剑桥切斯特顿路的家中暂住。

拉马努金很快就在剑桥安顿下来。四月底，他搬入了三一学院 Whewell’s Court 的宿舍，这里距离哈代的房间仅五分钟步行路程。尽管他并非正式学生，但他仍旁听了哈代以及国王学院数学家亚瑟·贝里（Arthur Berry）关于椭圆积分的讲座。在一次贝里的课上，拉马努金脸上兴奋的光芒引起了教授的注意。当被问及是否想补充什么时，他走上讲台，写下了贝里尚未证明、并且他此前不可能知晓的结果，令全场震惊。他立即开始了与哈代和利特尔伍德（Littlewood）的紧张工作，几乎每天都会向哈代展示半打新的定理。

然而，剑桥的生活远非一帆风顺。来自热带地区的拉马努金完全无法适应英格兰阴冷潮湿的气候，冬季时常病倒，一度连续五个月无法进行有效的科学研究。他严格的婆罗门戒律要求素食，且食物必须由同为婆罗门的人烹饪，这在战时的英国变得极其困难，他大多时候只能靠自己烹饪。文化的隔阂、食物的匮乏、战争的阴云以及深深的思乡之情，逐渐侵蚀着他的身心健康。在一次极度抑郁的爆发中，他甚至试图扑向地铁列车。1917年，他的健康彻底崩溃，被诊断出患有严重疾病（可能是肺结核或肝感染），此后大部分时间都在不同的疗养院中度过。

尽管病魔缠身，拉马努金的数学创造力却从未熄灭。他在病床上依然坚持研究。1918年，他的成就得到了最高认可：2月，他当选为剑桥哲学学会会员；5月，当选为英国皇家学会会士（FRS），成为最年轻的院士之一；10月，又当选为三一学院研究员，成为首位获此殊荣的印度人。这些荣誉仿佛一剂强心针，一度提振了他的求生意志，他甚至短暂地恢复了数学工作。在生命最后的时光里，他于1920年1月写给哈代最后一封信，概述了他最深奥的贡献之一——模拟Θ函数（Mock Theta Functions）的发现。

1919年，战争结束，拉马努金已是一个病入膏肓的人。他于2月27日至3月13日间踏上了返回印度的旅程。尽管马德拉斯大学已为他提供了优渥的研究津贴，但他于1920年4月26日与世长辞，年仅32岁。他在剑桥的五年虽是短暂一瞬，却彻底改变了现代数学的图景。他与哈代这位理性主义的无神论者结成了数学史上最不可思议的伙伴关系——一位依靠“女神在梦中给予公式”的直觉天才，与一位信奉严格证明的数学正统派。他们的合作，是一次不同文化、信仰和工作风格的激烈碰撞，也是最终绽放出最绚丽科学成果的完美互补。

数学成就与贡献

拉马努金在几乎无正规数学训练的背景下，对数论、无限级数、连分数、椭圆函数和分拆函数等领域做出了深远贡献。他独立提出了近3900个数学结果（多数为恒等式和方程），其中许多具有高度原创性和突破性，例如：

拉马努金素数：与素数分布相关的特殊素数。

拉马努金θ函数：影响模形式理论的发展。

分拆函数p(n)的渐进公式：与哈代合作提出，后被Rademacher证明。

模拟θ函数：临终前提出的深刻概念，启现代数几何与物理研究。

拉马努金在其1914年发表的论文《模方程与π的近似值》（Modular equations and approximations to π）中，提出了多个用于计算1/π的无穷级数。其中最著名且收敛速度极快的公式为：

该级数具有非凡的收敛特性。文档明确指出，其部分和收敛到π真值的速度在20世纪70年代之前是任何其他计算方法都无法比拟的。级数的每一项都能提供大约8位额外正确的小数位数。例如，仅计算首项（n=0）即可得到π的近似值精确到6位小数，而下一项（n=1）则能将精度提升至约14位小数。

超几何形式：

该公式的数学本质是椭圆积分与模函数理论的深刻应用，其推导源于拉马努金对q-级数和超几何函数的独创性研究。文档指出，这类公式是“椭圆积分的确切类比”，并体现了拉马努金将模函数理论应用于数论问题的非凡洞察力。

该公式的实际计算价值在计算机时代得到了极致发挥。Borwein兄弟在1986年使用拉马努金公式的一个变体，将π计算到了1700万位小数，并发现该公式的收敛效率远高于任何先前的方法。此后，基于拉马努金工作启发的算法（如文档中提到的“四次迭代算法”）被多次用于打破π的计算纪录，例如在2009年，一个团队利用此类算法在73小时内计算出了π的2.5万亿位小数。

拉马努金-楚德诺夫斯基公式 (Ramanujan-Chudnovsky Series)由Chudnovsky兄弟基于拉马努金的工作发现，是现代破纪录计算π的基础。

特性： 此级数的收敛速度比拉马努金的原公式更快，每一项可增加约14位十进制数的精度。该公式被用于计算π的数万亿位小数。

拉马努金还有提及了多个与π相关的级数公式，它们展示了拉马努金工作的广度。

公式A:

公式B:

公式C (与平方和表示相关):

注: 其中 是将整数k表示为两个平方和的方法数，是Ramanujan和。

除了级数，拉马努金也给出了高精度的代数近似公式，这些源于其“化圆为方”的几何研究。

近似式A (精确到9位小数):

近似式B (精确到16/18位小数):

近似式C:

拉马努金的工作方式依赖极强的直觉和归纳能力，常通过数值计算猜想定理，而非传统严格证明。尽管部分结论存在错误，但其主流成果已被广泛验证并融入现代数学体系。拉马努金的π级数不仅是其超凡数学直觉的例证——他甚至在缺乏严格证明的情况下就确信其正确性——更重要的是，它为现代计算数学提供了最强大的工具之一，彻底改变了高精度计算π的方式。

影响与遗产

拉马努金的工作对20-21世纪数学产生了深远影响：国际期刊《The Ramanujan Journal》专门发表受其影响的数学研究。印度设立“拉马努金奖”，其生平被改编为电影《知无涯者》（The Man Who Knew Infinity）。他的笔记本至今仍被数学家（如G.E. Andrews、B.C. Berndt）深入研究，推动数论、模形式等领域的发展。哈代评价其为“与欧拉、高斯并列的天才”，尽管缺乏正规教育，但其直觉与创造力无人能及。

总结

拉马努金在π的计算上留下了深刻的遗产，他的工作核心开创了基于模函数和椭圆函数的快速收敛级数，其收敛速度在计算机时代得到极致发挥。他提供了多种形式的公式，包括无穷级数和代数近似。他的思想直接启发了后来更强大的公式（如Chudnovsky公式），这些公式至今仍是计算π数十亿、数万亿位小数的算法基础。

解析与代数数论：问题驱动的探索之旅

数学并非仅是抽象符号与方程的集合，其最生动的应用往往体现在解决现实世界的问题之中。在解析数论与代数数论这一深邃的领域，传统的教科书常侧重于定理的逐一推导与证明，虽逻辑严谨，却可能让学习者陷入被动接受的困境，难以真切体会数学发现过程中的曲折与灵感迸发。M. Ram Murty 的这两本书尝试打破这一常规，秉承“一边做、一边学”的理念，将引导读者通过亲身求解一系列精心设计的问题，逐步探索整数的微妙性质与素数分布的奥秘。这种以问题串为主线、强调实践参与的学习模式，不仅能使抽象的数学概念变得生动具体，更能帮助学生在发展直觉、动手尝试、遭遇挫折、调整策略并最终解决问题的过程中，主动建构知识，深化对解析与代数数论核心思想的理解，最终提升独立研究的能力。

《Problems in Analytic Number Theory》

本书书名为《Problems in Analytic Number Theory》（解析数论中的问题），第二版。这本书是《Graduate Texts in Mathematics》（GTM）系列的第206卷，由Springer出版社出版。GTM系列是数学领域享誉盛名的研究生级教材系列，专注于提供严谨、深入的数学专题论述，旨在为研究生和研究人员提供高质量的学习与参考资源。该书作者M. Ram Murty是加拿大女王大学（Queen’s University）数学与统计系的教授，是一位在数论领域具有广泛影响和贡献的知名数学家。

本书的主题是解析数论，重点通过“问题-练习”的形式，引导读者深入理解该领域的核心概念与方法。内容覆盖了解析数论中的多个基本和高级主题，包括算术函数的性质、素数分布、Dirichlet级数、素数定理、函数方程、筛法、p进方法，以及第二版新增的等分布理论等。该书特别强调通过具体问题和练习培养读者的技巧和直觉，不仅提供理论框架，更注重如何将这些理论应用于解决数论中的具体问题。该书写作风格兼具教学性和研究性，既适合作为高年级本科生或研究生解析数论课程的教材，也适合作为研究人员自主学习和深化理解的工具书。书中包含大量精心设计的问题和练习，并配有详细的解答，帮助读者在实战中掌握解析数论的思想和方法。

M. Ram Murty的《解析数论问题》（Problems in Analytic Number Theory）正是这种理念的杰出代表。这本书的特色在于它完全颠覆了传统数学教材的呈现方式，

1. 以问题为核心的“做中学”模式 (Learning by Doing)

本书除了提供最基础的定义和概念框架外，几乎将所有重要的定理、命题和推导过程都转化为了一系列精心设计的习题（Exercises）。例如，素数定理（Prime Number Theorem）、Dirichlet定理（Primes in Arithmetic Progressions）、函数方程（Functional Equations）等解析数论的核心结果，其证明都不是直接给出的，而是被分解、引导，并通过习题让读者自己一步步完成。这种设计迫使读者从被动的知识接收者转变为主动的探索者和建构者。正如作者在序言中引用André Weil的观点：“仅仅掌握理论概念不足以充分欣赏一门学科，通常需要去解决那些这些思想被至关重要地使用的具体问题。” 掌握数学的真谛在于“先练习，后知识”（”it is practice first and knowledge afterwards”）。

2. 自我指导与研究能力的训练场

本书的目录清晰地分为两部分：第一部分（Part I）：问题（Problems）；第二部分（Part II）：解答（Solutions）。这种结构为读者提供了完整的自我指导学习路径。读者可以先尝试独立解决第一部分的难题，在遇到瓶颈时再参考第二部分的解答进行比对和学习。作者明确指出，本书的 singular purpose（唯一目的）是训练刚开始研究生学习的学生掌握解析数论的重要技巧。通过每日与这些问题“搏斗”（grappling），读者不仅能获得解析数论的知识，更能培养出自我指导学习（self-instruction）的纪律性，而这种能力对未来的研究工作是 indispensable（不可或缺的）。

3. 模块化与灵活的教学适配性

书籍的内容组织极具灵活性。作者建议了多种使用本书进行教学的方式： 本科高年级入门课程：可以专注于第1, 2, 3, 9, 10章。研究生初级课程：可额外涵盖第4, 5, 8章。高强度研究生课程：可以在一学期内覆盖全书，并将第6, 7, 10等更常规的章节交给学生进行报告（student presentations）。另一种模式：每周学习一章，由讲师聚焦于主要定理，并通过几个已解答的例子进行阐释。这种模块化设计使得一本书可以适应不同层次和不同进度的教学需求。

4. 覆盖广泛且深刻的“基础工具包”

本书内容极为丰富，从算术函数、素数分布、 contour积分、函数方程、Hadamard乘积、显式公式，到更专门的筛法（Sieve Methods）、p-adic方法，乃至第二版新增的等分布（Equidistribution）理论，几乎涵盖了现代解析数论的所有基础工具和核心课题。作者坦言，虽然许多重要课题被省略了，但所包含的材料是每一位数论学家所需的 “基础工具包”（”basic tool kit”） ，而其中较难的习题则揭示了该领域精妙的“技巧诀窍”（”tricks of the trade”）。

总结而言，M. Ram Murty的这本书通过其独特的“全习题化”架构，成功地将一本教材转变为一座连接理论知识与研究实践的桥梁。它不仅仅是在传授解析数论的内容，更是在传授如何发现、探索和最终理解这些内容的方法论，完美体现了“授人以渔”的教学最高境界。这种模式为编写高级数学领域的教科书提供了一个非常成功且值得效仿的范本。

《Problems in Algebraic Number Theory》

这本书《代数数论问题》（Problems in Algebraic Number Theory）的核心特点是以“做中学”（Learning by Doing）为教学理念，强调通过具体问题的提出与解决来引导学习者深入理解代数数论的核心概念与方法。全书的结构与内容设计均围绕这一理念展开，同样具有以下鲜明特点：

1. 问题驱动的学习路径

书中通过系统编排的500多个问题，循序渐进地揭示代数数论中概念与思想的演变。每个章节从基础问题入手（如整数的唯一分解、欧几里得环的性质），逐步过渡到更复杂的主题（如理想类群、二次互反律、密度定理），使学习者在解决问题的过程中自然构建知识体系，而非被动接受抽象理论。

2. 通过示例深化理论理解

作者在前言中引用牛顿和Lichtenberg的观点，强调“通过例子学习比通过规则学习更有效”。书中每个问题都配有完整的解答，确保学习者在自主尝试后能获得即时反馈，并通过对比解答来修正思路、填补知识漏洞。这种设计鼓励学习者主动探索定理的细微差别和应用场景，从而形成深刻直觉。

3. 适合独立学习的自洽性

全书内容设计为适合一学期独立学习，任何具备本科代数背景的学习者均可自主使用。问题与解答的紧密结合降低了外部指导的依赖，学习者可通过反复练习和验证来强化推理能力，真正实现“在脑海中开辟一条可重复使用的路径”。书中不仅传授知识，更注重培养研究能力。通过引导学习者从简单问题中发现规律、逐步推广到复杂问题（如从费马小定理到ABC猜想的应用），模仿了实际数学研究中的问题提出与解决过程。这种训练帮助学习者掌握“提出正确问题”的艺术，而非仅仅记忆结论。新增的密度定理章节体现了“代数方法与解析方法的壮丽交互”，通过问题展示如何将抽象理论（如Dedekind ζ函数）应用于具体问题（如素数分布）。学习者在解决这些问题的过程中，自然领悟到理论的实际意义与威力。

总之，这本书通过问题与解答的有机组合，将“做中学”的理念贯穿始终，使代数数论的学习不再是被动接受，而是主动探索、实践和发现的过程。这种设计不仅夯实了理论基础，更培养了学习者独立研究和创造性思维的能力。