Nicolas Bourbaki 是一个由一群数学家组成的集体笔名，主要由法国巴黎高等师范学院（École normale supérieure, ENS）的校友组成。该团体成立于1934年至1935年，最初目的是编写一本新的分析学教科书。随着时间的推移，项目变得更加宏大，发展成为一系列以 Bourbaki 名义出版的教科书，旨在涵盖现代纯数学的各个领域。这一系列著作统称为《数学原理》（Éléments de mathématique），是 Bourbaki 的核心作品，内容涉及集合论、抽象代数、拓扑学、分析学、李群和李代数等。

背景与成立

Bourbaki 的名字来源于19世纪法国将军 Charles-Denis Bourbaki，他在普法战争中经历了戏剧性的失败。这个名字在20世纪初的法国学生中广为人知。1935年夏天，小组决定采用”尼古拉·布尔巴基”这个集体笔名。这个名字源自1870年普法战争中法国将军夏尔·索泰尔·布尔巴基。更滑稽的是，这个典故来自巴黎高师的一场恶作剧讲座——高年级学生拉乌尔·胡森假扮数学家，用假胡子和浓重口音宣讲了一堆以法国将军命名的错误定理，最后最荒谬的定理被命名为”布尔巴基定理”。

Bourbaki 的成立是对第一次世界大战后法国数学界人才断层现象的回应。战争导致一代法国数学家丧生，年轻教师被迫使用过时的教材。Henri Cartan 和 André Weil 等人在斯特拉斯堡大学任教时，对现有教材的不满促使他们召集其他数学家共同编写现代分析学教材。创始成员包括 Henri Cartan、Claude Chevalley、Jean Delsarte、Jean Dieudonné 和 André Weil 等。1934年，29岁的亨利·嘉当和27岁的安德烈·韦伊在斯特拉斯堡大学任教时，因对传统教材《Goursat分析教程》不满，萌生了编写新分析教材的想法。他们与巴黎高师校友们在圣米歇尔大道的卡普拉德咖啡馆定期聚会（每周一中午），这个充满咖啡香气的空间成为了现代数学史上最具影响力的学术沙龙。

工作方式

Bourbaki 定期举行私人会议，讨论和起草《数学原理》的内容。主题分配给小组委员会，草案经过激烈辩论，只有全体一致同意后才会出版。尽管过程缓慢且费力，但这种方法确保了作品的严谨性和普适性。Bourbaki 还组织 Séminaire Bourbaki，定期举办讲座并出版讲义。疯狂的科学聚会：1935年7月在贝斯昂尚德塞举行的第一次布尔巴基大会上，成员让·迪厄多内后来描述道：”初次参会者总会觉得这是一群疯子的聚会”。会议没有主席，所有人可以随时打断发言，常常三四个人同时 shouting，但这种”精心设计的混乱”恰恰成为他们创造性思维的源泉。韦伊解释说，任何组织化的尝试都会让著作变得平庸。1938年小组将著作命名为《数学原理》(Éléments de Mathématique)，故意去掉通常法语中”数学”(Mathématiques)的词尾”s”，用这个语法细节宣示他们对数学统一性的信仰，这个细节后来成为科学史上最著名的”缺失的S”。

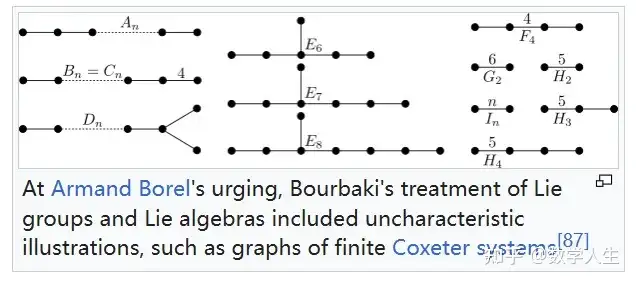
1940年代末新成员Armand Borel首次参加Bourbaki会议时，被现场震撼——成员们用”最高音量喊出两三个独立进行的独白”，尤其是大嗓门的Dieudonné总能让讨论升级为”混乱的喊叫比赛”。这种独特的审稿方式要求每个章节被逐行朗读，任何人都可随时打断批评，形成一种既混乱又高效的协作模式。Dieudonné强调成员必须对”听到的一切都感兴趣”，拒绝只专精某一领域的”狂热代数家”。成员常被要求撰写非本专业的章节，比如代数专家写拓扑章节，这种”通才培养”模式让许多人受益匪浅，但也引发后来关于”是否需天才才能胜任”的争议。

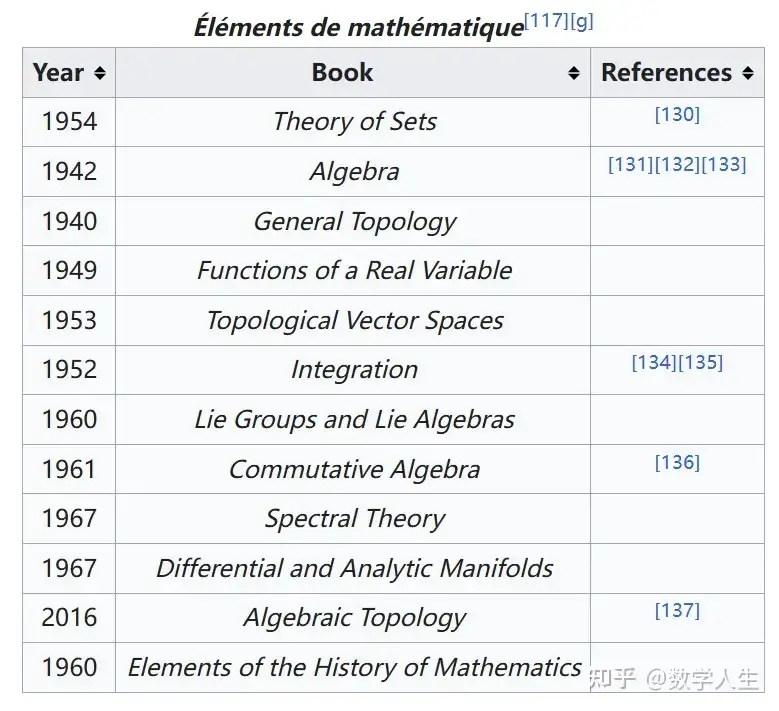
原计划按顺序出版6本书，实际却呈现”大杂烩”式出版：1947年先出《拓扑学》第5-7章，1948年突然跳回《代数》第3章讲张量积，1949年又穿插《实变函数》的泰勒定理，完全打乱编号体系。这种看似混乱的进程反而展现了他们对数学整体性的追求。1950年代新加入的Grothendieck坚持”百科全书式写作”，提案用超代数等前沿理论为流形奠基，结果被吐槽”过于抽象，可能让我们陷入基础工作多年”。年轻成员Cartier后来直言早期著作”当教材是灾难”，反映了代际认知差异。

影响与批评

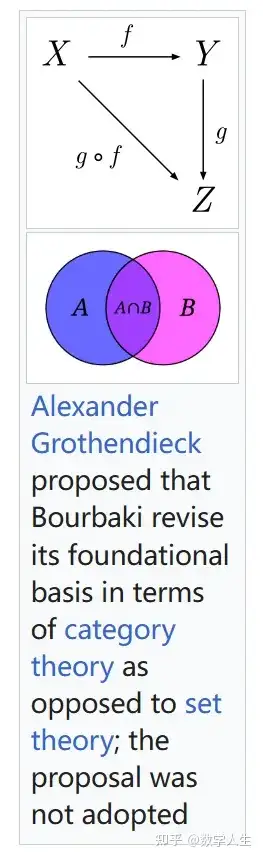
Bourbaki 学派以极端严谨的公理化方法著称，强调数学结构的分类（代数结构、序结构、拓扑结构），并主张从最一般的形式推导特殊案例。其独特的“布尔巴基风格”表现为高度抽象、排斥直观图示与计算，追求逻辑上的完备性。例如，实数被定义为拓扑群的完备化，而非直接从有理数构造。Bourbaki 在20世纪中叶对数学产生了深远影响，尤其是在数学结构的引入和严格化方面。其作品影响了“新数学”（New Math）教育改革运动，但由于过于抽象而受到批评。Bourbaki 的风格强调公理化和抽象化，但也因忽视应用数学和某些现代数学领域（如范畴论）而受到批评。

成员与传承

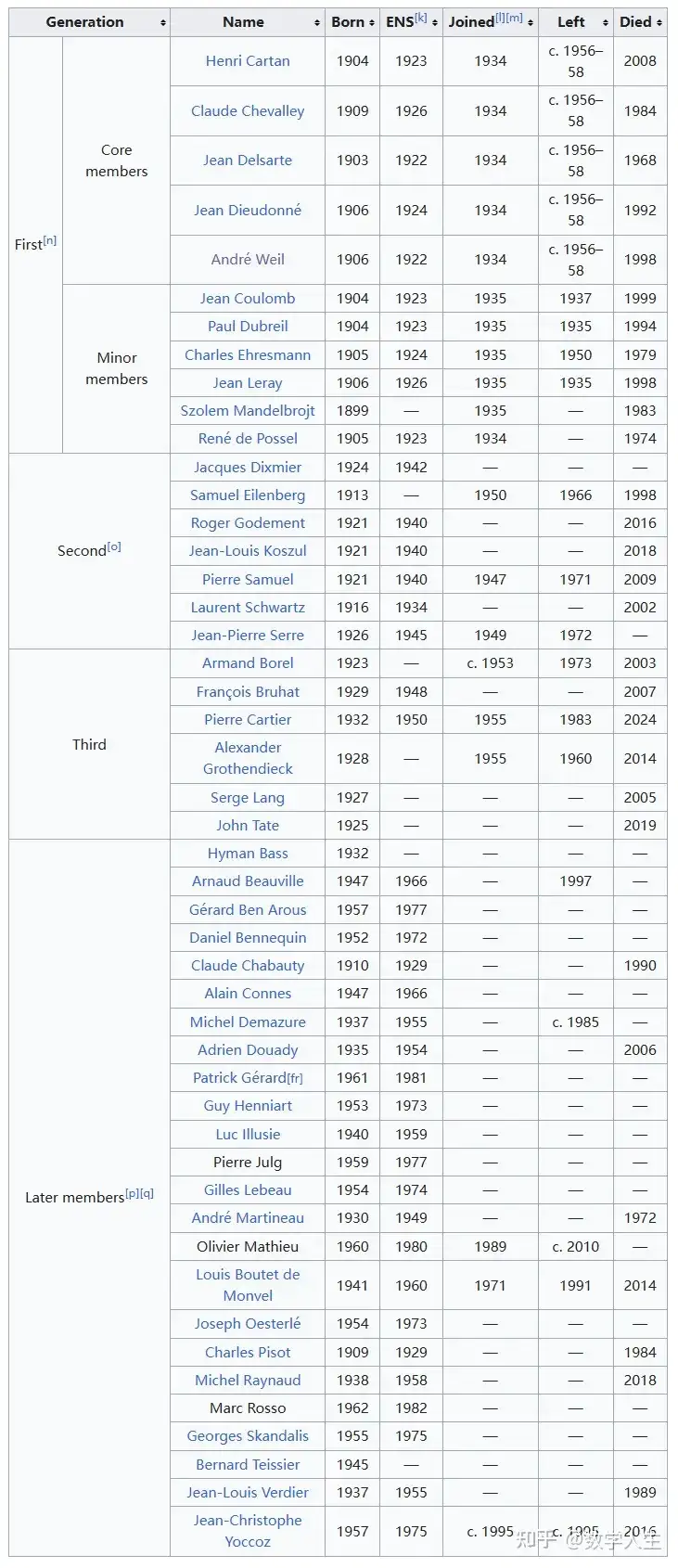
Bourbaki 的成员身份保密，历史上约有40名成员，通常保持10至12人的规模。成员按“代际”更替，创始成员逐渐退出，由年轻数学家接替。尽管 Bourbaki 的影响力在20世纪后期有所下降，但其对数学教育的贡献和严谨的数学方法仍被广泛认可。自2012年以来，Bourbaki 恢复了《数学原理》的出版，修订了部分章节并新增了代数拓扑和谱理论等内容。2023年出版了关于谱理论的新卷，并宣布正在准备范畴论和模形式的新书。Bourbaki 不仅是一个数学团体，更是一种数学文化和方法的象征，其作品和思想至今仍在数学界引起讨论和反思。

历史活动

布尔巴基研讨会是自1948年起在巴黎举行的系列公开讲座，以数学家集体笔名“尼古拉·布尔巴基”命名。以下是1948/49和1949/50两个年度的研讨会内容概述：

1948/49系列

1. Henri Cartan：Koszul的工作（I-III）——李代数上同调。
2. Claude Chabauty：Minkowski-Hlawka定理（数论中的格点问题）。
3. Claude Chevalley（I-II）：Weil的代数函数域上的黎曼假设（局部ζ函数）。
4. Roger Godement（I-II）：复单模群的不可约酉表示（Gelfand和Neumark的工作）。
5. Léo Kaloujnine（两次）：有限对称群的Sylow p-子群结构及无限推广。
6. Pierre Samuel & Luc Gauthier：Zariski的双有理对应理论（代数几何）。
7. Jean Braconnier：有限群的自同构塔（Wielandt的工作）。
8. Laurent Schwartz（两次）：Petrowsky的偏微分方程柯西问题研究。
9. André Weil：Poincaré和Frobenius的θ函数基本定理。

特点：

主题涵盖代数几何、群论（有限群与无限群）、表示理论、偏微分方程等。多次重复同一主题（如Koszul、Zariski、Petrowsky的工作），显示深度探讨。

1949/50系列

1. André Blanchard：Kolchin的微分伽罗瓦理论。
2. Jean Dieudonné：Chow的齐次代数空间几何。
3. Roger Godement（I-II）：希尔伯特空间的连续和（泛函分析）。
4. Charles Pisot：Selberg和Erdös的素数定理初等证明。
5. Georges Reeb：动力系统的轨迹性质。
6. Pierre Samuel：局部环与代数几何导论。
7. Marie-Hélène Schwartz：Heins的解析函数与次调和函数增长性研究。
8. Charles Ehresmann：微分纤维丛中的无穷小联络。
9. Laurent Schwartz（四次）：Kodaira的黎曼流形调和场（Hodge理论）。
10. Jean-Pierre Serre & Armand Borel：Iwasawa和Gleason的局部紧群扩张。
11. Jacques Dixmier：冯·诺依曼代数的分类与迹。
12. Jean-Louis Koszul：Jordan代数。

特点：

新增微分几何（纤维丛联络）、动力系统、调和分析（Hodge理论）等方向。更强调分析学与几何的结合（如Kodaira的工作）。

1950-1959系列

后续研讨会按十年分期延续了这一传统（如1950-1959、1960-1969等）。出版方包括巴黎大学、Springer-Verlag和法国数学学会（Astérisque系列）。 布尔巴基学派（Nicolas Bourbaki）在1950-1959年间的研讨会（Séminaire Nicolas Bourbaki）涵盖了广泛的数学领域，反映了该学派在这一时期对现代数学的深远影响。以下是这十年间研讨会的主要内容和研究方向总结：

1. 主要研究方向

代数几何：包括Jacobian簇、Picard簇、Hilbert第十四问题、Zariski理论、复乘法和代数曲面等。Grothendieck的下降理论和形式模理论为现代代数几何奠定基础，Zariski和Weil的工作推动了算术几何的发展。

拓扑学：涉及同伦群、纤维丛、上同调理论、Steenrod运算、配边理论（Thom、Milnor）以及Bott周期性定理。Thom的配边理论和Bott周期性定理影响了微分拓扑和K-理论。

李群与表示论：包括半单李群、Harish-Chandra的工作、诱导表示、球函数、紧李群及其在齐次空间上的作用。Harish-Chandra的半单李群表示理论和Godement的zeta函数研究推动了自守形式的发展。

微分几何：研究Kähler流形、Hermitian对称空间、齐次空间的微分几何、等距嵌入（Nash-Kuiper）等。

数论与类域论：涉及Weil猜想、局部类域论、Iwasawa理论、adelic环和代数数域的扩张。Iwasawa理论、Weil猜想和Dwork的zeta函数理性证明标志着现代数论的转折点。

偏微分方程：包括椭圆方程、Cauchy问题、Navier-Stokes方程、Malgrange和Hörmander的工作。Malgrange、Lions和Hörmander的工作为线性与非线性PDE提供了重要工具。

泛函分析：拓扑张量积、核空间（Grothendieck）、von Neumann代数、Banach代数中的符号计算等。

逻辑与计算理论：图灵机、不可判定问题（Tamari）、谓词逻辑的语义表（Guillaume）。

2. 重要人物与贡献

Alexander Grothendieck：在代数几何（下降理论、对偶定理）、拓扑张量积和形式几何方面做出奠基性工作。

Jean-Pierre Serre：涉及同伦论、类域论、Steenrod运算、zeta函数的理性（Dwork）以及Borel-Weil定理。

Armand Borel：研究代数群、齐次空间、Hermitian对称空间和紧李群。

René Thom：在配边理论、微分映射的奇点理论以及浸入分类（Smale）方面做出贡献。

Jacques-Louis Lions：研究位势理论、椭圆边值问题、Navier-Stokes方程和插值理论。

André Weil：涉及类域论、复乘法、Torelli定理以及adele代数群。

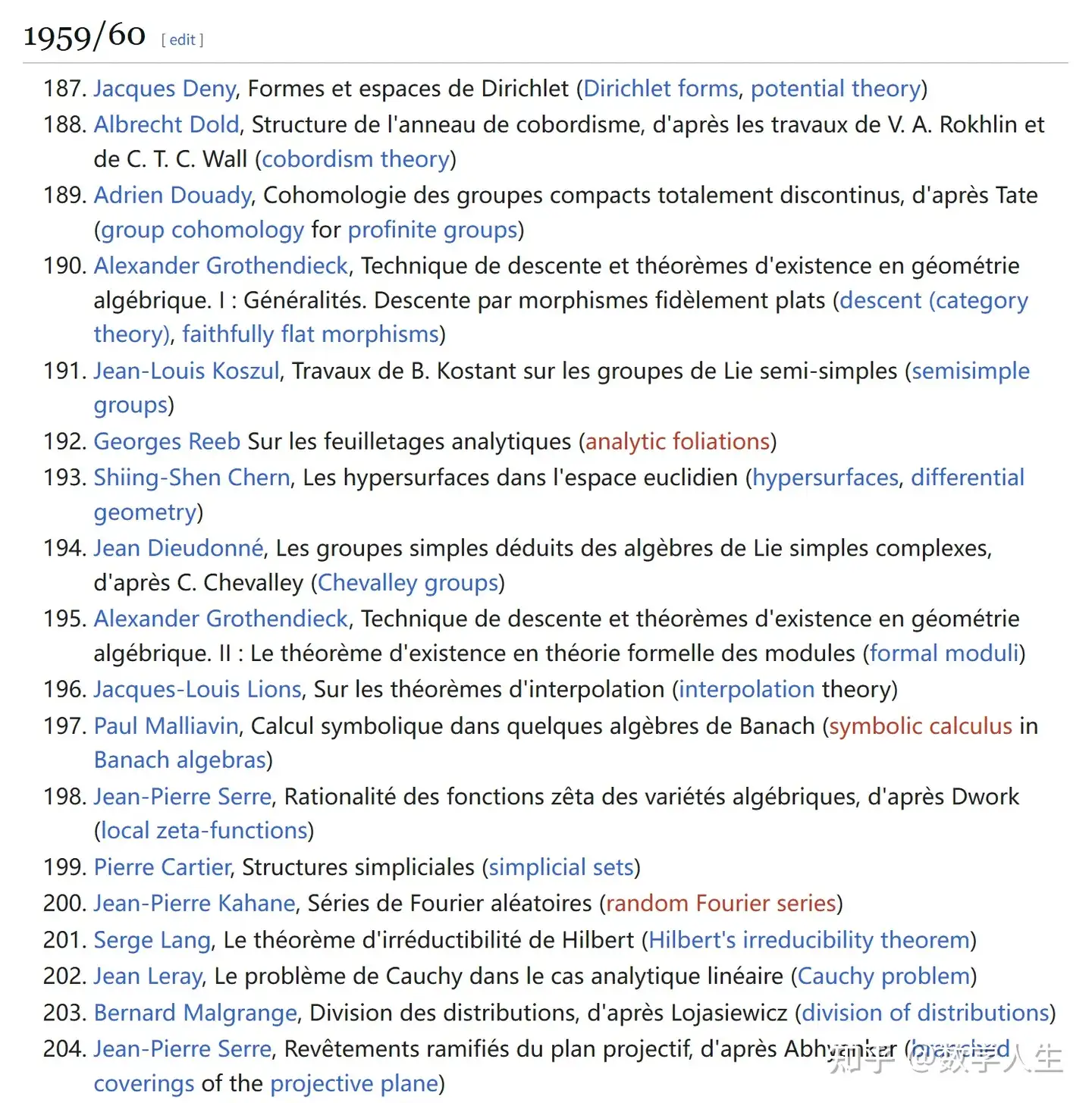
1960-1969系列

这一时期的研究为20世纪下半叶数学的发展奠定了坚实基础，尤其是代数几何、表示论和拓扑学的革命性进展。 布尔巴基学派（Nicolas Bourbaki）在1960-1969年间的研讨会（Séminaire）涵盖了广泛的数学主题，反映了当时数学研究的前沿方向。

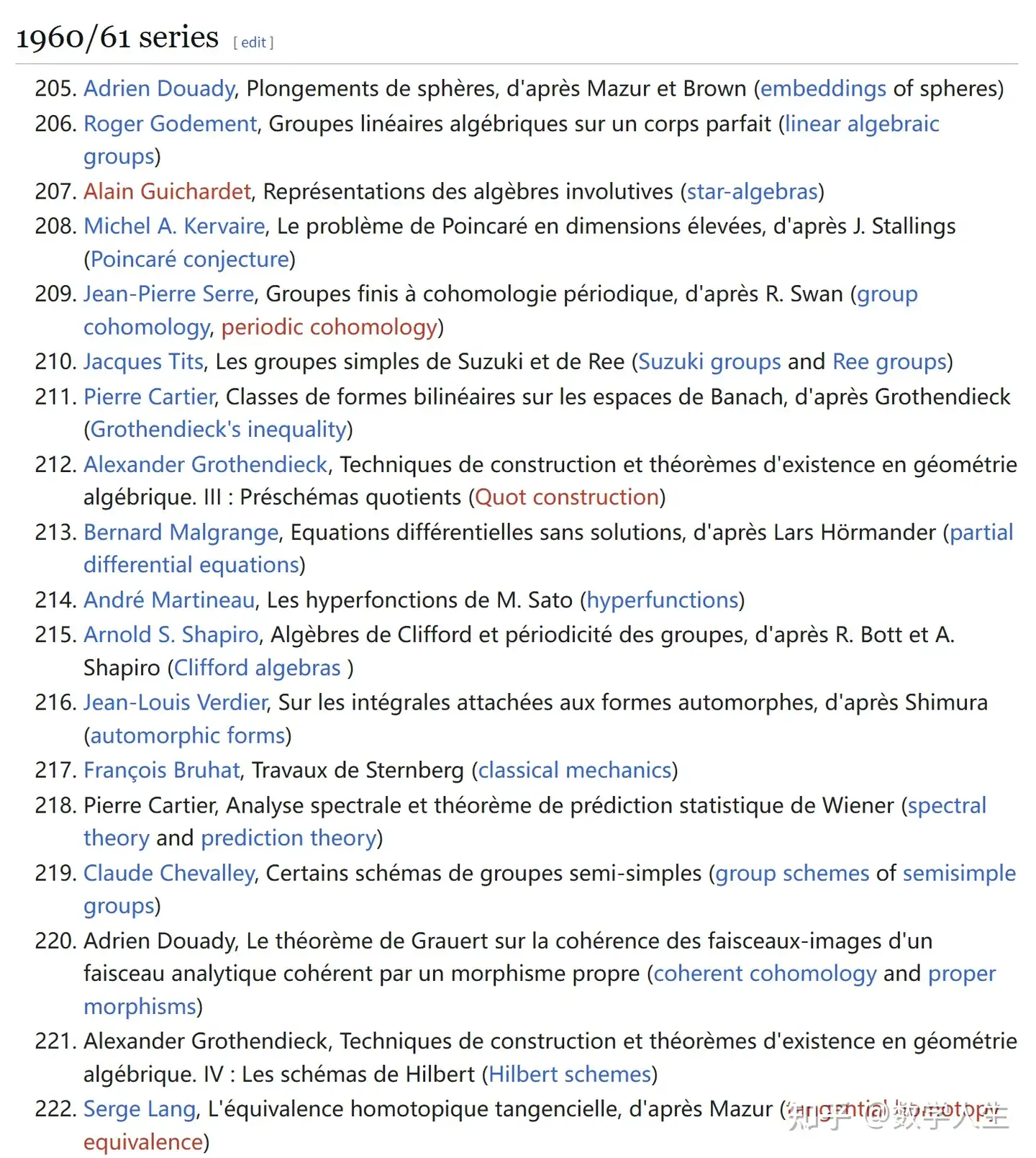
1. 主题多样性

代数几何：Alexander Grothendieck 的贡献尤为突出，涉及 Hilbert 概形、Picard 概形、下降技术（descent techniques）以及 Brauer 群等。

拓扑学：包括 Bott 周期性定理、球面嵌入（embeddings of spheres）、向量场（vector fields on spheres）以及 Poincaré 猜想在高维的情况（由 Kervaire 和 Stallings 的工作）。

微分几何与代数拓扑：如 Nash 嵌入定理（Nash embedding theorem）、Chern 定理（Chern’s theorem）以及微丛（microbundles）。

表示论与李群：包括半单群的表示（Roger Godement、Claude Chevalley）、Kirillov 的轨道方法（nilpotent Lie groups）以及 p-adic 李群（Jean-Pierre Serre）。

数论与算术几何：如 Néron 模型（André Néron）、Mordell 猜想（Pierre Samuel）以及自守形式（automorphic forms，由 Shimura 和 Langlands 的工作）。

分析：包括偏微分方程（Bernard Malgrange、Lars Hörmander）、调和分析（Jean-Pierre Kahane、Paul Cohen）以及奇异积分算子（Laurent Schwartz）。

逻辑与计算：如不可判定性定理（Daniel Lacombe）。

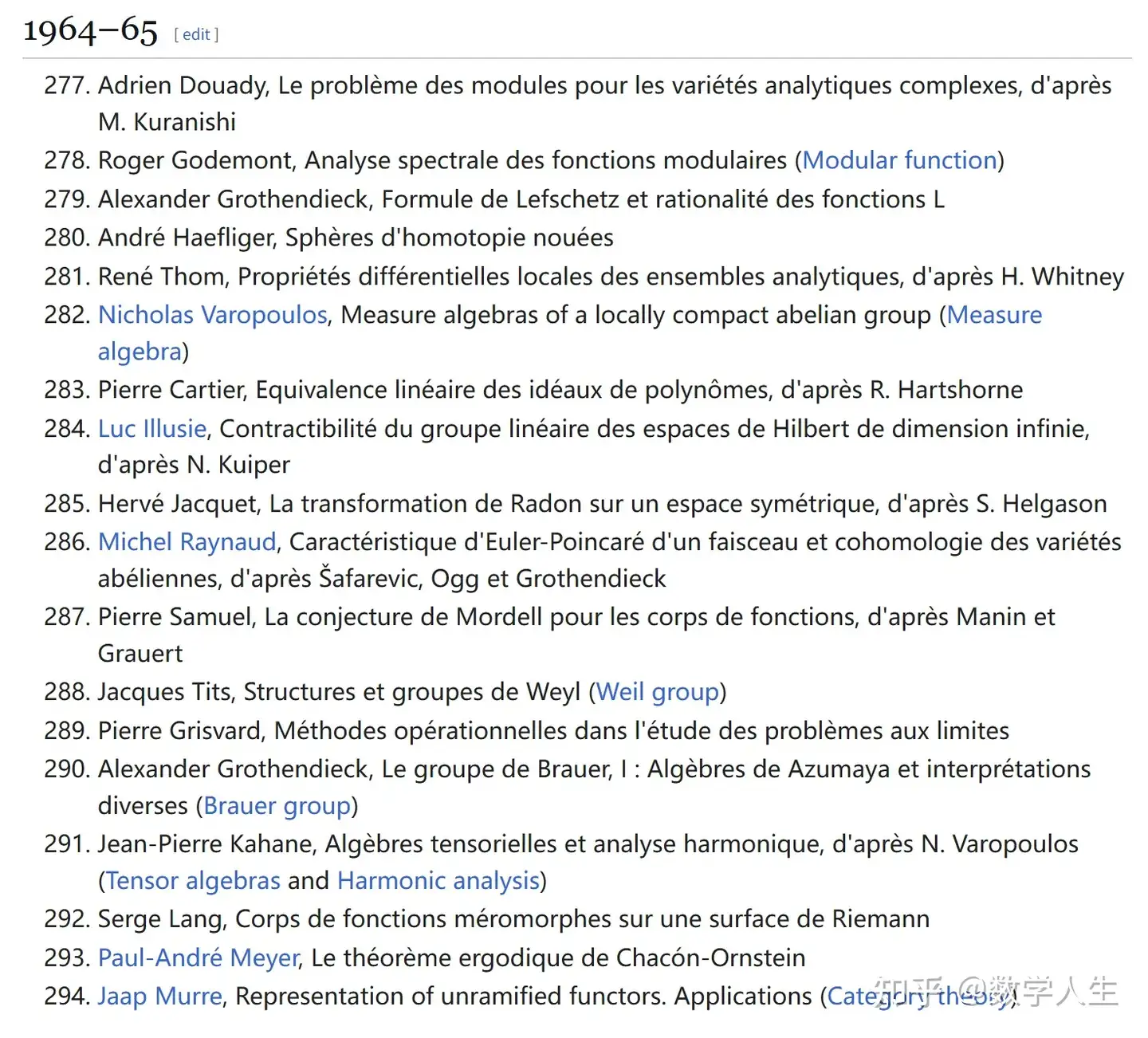
2. 重要人物与贡献

Alexander Grothendieck：主导了代数几何的多个方向，包括概形理论、下降技术和 Brauer 群。

Jean-Pierre Serre：涉及群上同调（group cohomology）、p-adic 李群和有限群的研究。

Roger Godement：研究了线性代数群、Selberg 迹公式（Selberg trace formula）以及模函数（modular functions）。

Bernard Malgrange：专注于偏微分方程和椭圆边值问题（elliptic boundary value problems）。

Adrien Douady：贡献于复几何（如 Kuranishi 的模空间理论）和拓扑（如 Bott 周期性定理）。

Pierre Cartier：涉及随机过程（stochastic processes）、表示论和代数群。

3. 标志性成果

Atiyah 的椭圆算子指标定理（1962-63）：由 Michael Atiyah 介绍，成为微分拓扑的重要工具。

Bott 周期性定理（1963-64）：由 Adrien Douady 介绍，推动了 K-理论的发展。

Nash 嵌入定理（1961-62）：由 Serge Lang 介绍，解决了黎曼流形的等距嵌入问题。

Langlands 的自守形式研究（1963-64）：由 Hervé Jacquet 介绍，为朗兰兹纲领奠定了基础。

1960-1969 年的布尔巴基研讨会是现代数学发展的一个缩影，涵盖了从代数几何到分析、从拓扑到数论的广泛领域。其特点是理论深度与跨学科性，许多主题至今仍是研究热点。Grothendieck、Serre 和 Atiyah 等数学家的贡献尤为突出，推动了 20 世纪数学的重大进展。

朗道（Lev Davidovich Landau, 1908-1968）是20世纪最杰出的理论物理学家之一，他的贡献涵盖了理论物理学的几乎所有领域，从量子力学到凝聚态物理，从核物理到流体力学。他的工作不仅推动了物理学的发展，还通过他的教学和指导培养了一代又一代的物理学家。

生平简介

列夫·达维多维奇·朗道（Lev Davidovich Landau，1908年1月22日－1968年4月1日）是苏联著名理论物理学家，出生于俄罗斯帝国巴库（今阿塞拜疆首都）的一个犹太家庭。他自幼展现出非凡的数学天赋，12岁掌握微积分，14岁进入巴库大学同时学习物理和化学，后专注于物理学。1924年转入列宁格勒大学（今圣彼得堡国立大学），1927年毕业后赴欧洲游学，曾在哥本哈根尼尔斯·玻尔研究所工作，深受玻尔影响。1932年至1937年，他在乌克兰哈尔科夫的物理技术研究所领导理论物理部门，创立了著名的“朗道学派”。1937年移居莫斯科，担任苏联科学院物理问题研究所理论部主任直至1962年。1968年因车祸后遗症去世，葬于莫斯科新圣女公墓。

主要科学贡献

朗道的研究涵盖理论物理几乎所有领域，被誉为“最后一位全能物理学家”。朗道的科学贡献横跨多个领域，他的理论不仅深刻影响了20世纪的物理学，至今仍在多个研究方向中发挥重要作用。他的教育理念和科学精神也激励了无数物理学家。1962年，他因“凝聚态物理的开创性理论，特别是液氦的超流性”获得诺贝尔物理学奖。尽管他在1962年的车祸后健康严重受损，但他的科学遗产仍在继续推动物理学的发展。他的核心成就包括：

1. 量子力学与量子场论

朗道在量子力学的早期发展中做出了重要贡献。1927年，他在研究辐射阻尼问题时首次引入了密度矩阵的概念，这一工具后来成为量子统计力学和量子信息理论的基础。1930年，他与佩尔斯（R. Peierls）合作研究了相对论量子力学中的测量限制，提出了在相对论情况下动量测量的不确定性原理的扩展。这一工作为后来的量子场论奠定了基础。

在量子场论方面，朗道与阿布里科索夫（A. Abrikosov）和哈拉特尼科夫（I. Khalatnikov）合作，研究了量子电动力学中的发散问题。他们提出了一种“点相互作用”的极限处理方法，并发现当相互作用半径趋近于零时，理论会“归零化”（即有效电荷趋于零）。这一发现对量子场论的重整化理论产生了深远影响。

2. 凝聚态物理

朗道在凝聚态物理领域的贡献尤为突出，尤其是在超流性和超导性的研究上。1941年，他提出了液氦II的超流理论，解释了为什么液氦在极低温下可以无摩擦流动。他引入了准粒子（元激发）的概念，将液氦的能谱分为声子（phonon）和旋子（roton）两种模式，并建立了二流体模型，即超流体和正常流体的共存理论。这一理论不仅解释了超流现象，还为后来的玻色-爱因斯坦凝聚研究提供了重要参考。

1950年，他与金兹堡（V. L. Ginzburg）合作提出了超导的唯象理论（Ginzburg-Landau理论），该理论通过引入序参量（order parameter）描述了超导相变。这一理论后来被BCS理论（微观超导理论）所证实，并成为研究超导体的重要工具。

3. 相变理论

1937年，朗道提出了二级相变的一般理论，这是他对统计物理学的重大贡献。他引入了序参量的概念，并指出相变的发生与系统对称性的变化密切相关。他的理论不仅适用于超导和超流，还广泛应用于铁磁、铁电和液晶等系统的研究。朗道的相变理论为现代凝聚态物理提供了重要的理论框架。

4. 等离子体物理与流体力学

朗道在等离子体物理方面的贡献包括朗道阻尼（Landau damping）的发现。1946年，他证明即使在无碰撞的等离子体中，高频振荡也会因粒子与波的共振相互作用而衰减。这一现象对等离子体物理和受控核聚变研究具有重要意义。

在流体力学领域，他研究了湍流的起源，提出了层流失稳后流动发展的定性理论。他还发现了超音速流动中的双重激波结构，并给出了粘性不可压缩流体轴对称射流的精确解。

5. 核物理与粒子物理

朗道在核物理方面提出了液滴模型，将原子核视为量子液体，这一模型后来被用于解释核裂变和核结构。在粒子物理领域，他在1956年提出了二分量中微子理论，预言中微子具有固定的螺旋性（helicity），并提出了“联合宇称”（CP守恒）的概念。尽管后来发现CP对称性在某些弱相互作用中也会破缺，但他的理论对粒子物理的发展产生了深远影响。

6. 教育与科学传承

朗道不仅是一位伟大的科学家，还是一位杰出的教育家。他设计了“理论物理最低标准”（Theoretical Minimum）考试，要求学生在数学和物理的各个方面达到高标准。他的《理论物理学教程》（与栗弗席兹合著）至今仍是全球物理学学生的经典教材。他的学生中有多位成为苏联科学院的院士，包括阿布里科索夫、哈拉特尼科夫等著名物理学家。

7. 个人风格与影响

朗道以其敏锐的物理直觉和追求简洁的思维方式著称。他常说：“物理学家的工作是‘平凡化’（trivialize）复杂的问题。”他的科学风格强调物理本质，而非数学形式。他还以幽默著称，曾对数理物理学家进行“等级排名”，将自己列为“2½级”，而爱因斯坦是“½级”。

Landau Genius Scale

朗道天才标度（Landau Genius Scale）是苏联物理学家列夫·朗道（Lev Landau）在20世纪30年代提出的一种对理论物理学家创造力进行分级评价的体系。该标度以对数形式衡量物理学家的贡献，每差一级代表贡献相差10倍。

1. 标度分级与代表人物

0级：最高级别，仅牛顿一人入选，被誉为“近代物理学之父”。

0.5级：爱因斯坦，被认为略逊于牛顿，但仍是“物理巨匠”。

1级：量子力学奠基人，包括玻尔、海森堡、狄拉克、薛定谔，以及费米、德布罗意、玻色、维格纳等。

1.5-2.5级：朗道最初自评为2.5级，获诺贝尔奖后调整为2级，晚年升至1.5级。

3-5级：涵盖其他知名物理学家，如费曼被认为与朗道相近（约2级），而杨振宁未被朗道正式评分，但后人推测其应属1级。

2. 标度的数学意义

以10为底的对数标度，即一流（1级）物理学家的贡献是二流（2级）的10倍，超一流（0级）是一流的10倍。朗道认为牛顿的贡献是爱因斯坦的10倍（因0级与0.5级的对数差）。

3. 争议与补充

杨振宁的定位：朗道未直接评价杨振宁，部分因其成就多在朗道去世后显现。后人分析其“杨-米尔斯理论”等贡献应属1级，与量子力学奠基人并列。主观性与局限性：标度反映朗道个人观点，虽在科学界有一定认可度，但也因“傲慢”引发争议（如将5级称为“病态”）。

4. 其他分类方式

朗道还曾用数学算符比喻物理学家类型，如：拉普拉斯算子（聪明且专注）：玻尔、爱因斯坦；菱形算子（聪明但浮躁）：自称；梯度算子（浮躁且平庸）：如伊万年科。

朗道标度以对数形式量化物理学家的历史地位，核心逻辑是“创造力差距的指数级差异”。尽管主观性强，但其对牛顿、爱因斯坦等“开派宗师”的定位与科学史共识高度一致。

教育与学术遗产

朗道设计了严苛的“理论物理最低标准考试”，1934-1961年仅43人通过，其中包括多位未来著名物理学家（如阿布里科索夫、栗弗席茨）。他与学生合著的十卷本《理论物理学教程》至今仍是经典教材。他提出的“物理学家天才对数标度”将牛顿评为最高级（0级），爱因斯坦为0.5级，自评为2级，成为科学界的趣谈。朗道性格幽默尖锐，持无神论和社会主义立场。他参与苏联核武器研发，获斯大林奖（1949、1953）和“社会主义劳动英雄”称号（1954）。1962年，朗道遭遇严重车祸，虽幸存但丧失科研能力，同年获诺贝尔物理学奖（因超流理论），由其学生代领。1968年逝世，身后留下对苏联科学的深远影响，其思想与人格矛盾（天才的傲慢）成为传奇。他的KGB档案于1991年公开，揭示了日常生活与学术成就交织的复杂一生。为纪念他，俄罗斯科学院设立“朗道金质奖章”，月球陨石坑和小行星2142均以其命名。