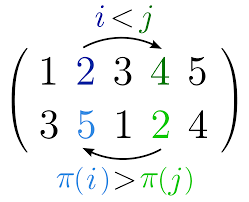群论

群论是数学中研究对称性的核心分支，它通过抽象的代数结构描述物体、方程或物理系统的对称操作。有限群，即元素个数有限的群，在数学和科学中无处不在，从晶体结构的对称性到密码学的加密算法，再到粒子物理的标准模型，都能看到它们的身影。

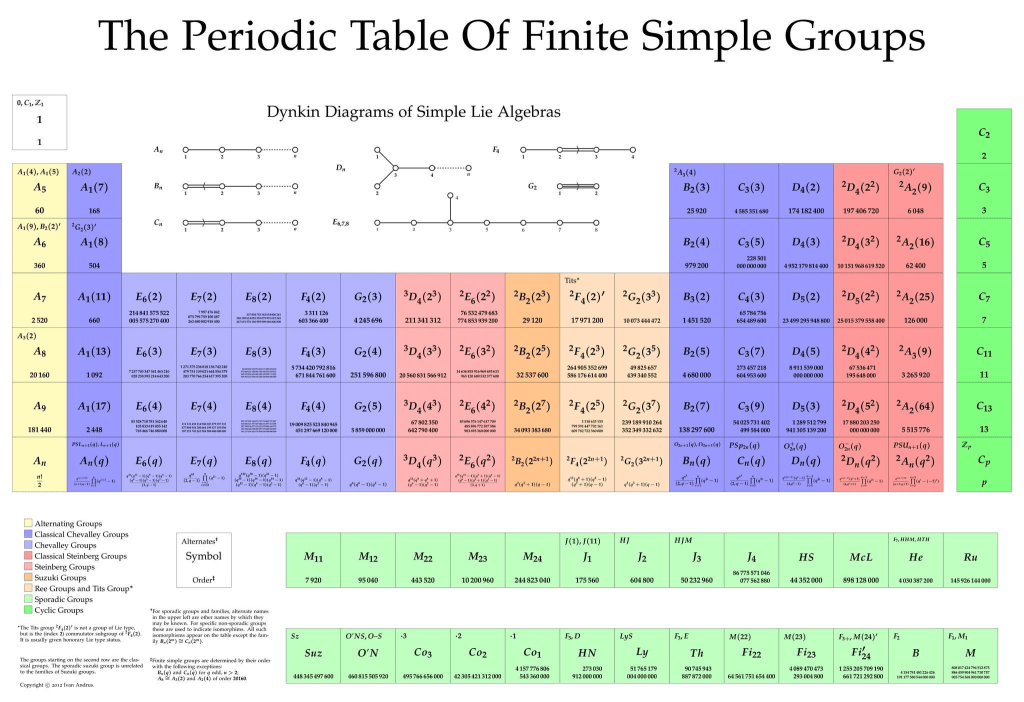
而有限单群作为群论中的“基本粒子”，扮演着至关重要的角色——它们无法被分解为更小的群的直积，因此构成了所有有限群的构建基石。有限单群的分类定理被誉为20世纪数学最伟大的成就之一，它证明了所有有限单群都归属于四大类别：素数阶循环群、交错群、李型群和26个散在单群。这一分类不仅解决了数学中一个根本性的结构问题，还为其他领域提供了强大的工具。例如，李型群与几何和数论中的模形式紧密相连，而最大的散在单群“魔群”甚至与弦理论中的高维物理模型产生了意想不到的联系。该定理的证明历时超过一个世纪，涉及数百位数学家，总证明长度超过一万页，堪称数学界的“曼哈顿计划”。尽管分类已经完成，其影响仍在持续发酵——数学家们仍在努力简化证明、探索散在群的神秘性质，并寻找这些抽象结构在现实世界中的新应用。有限单群的分类不仅是纯粹数学的巅峰之作，更是人类理解对称性和宇宙基本结构的里程碑。

有限单群分类

有限单群是群论中的基本构件，类似于数论中的素数——它们无法被分解为更小的群的直积。20世纪，数学家们完成了有限单群的完全分类，这是数学史上最庞大的证明之一，涉及数百位数学家的合作，最终将所有有限单群划分为四个明确的类别。

一个有限单群（finite simple group）是指一个有限的群 ，它没有非平凡的正规子群（即除了 和 本身之外）。这意味着它不能分解为更小的群的直积或半直积。单群在群论中的作用类似于素数在数论中的作用——它们是构建更复杂群的基本“原子”。

19世纪末：问题的萌芽

1870年，法国数学家 Camille Jordan 首次系统研究单群，发现 （）和某些线性群是单群。1892年，德国数学家奥托·赫尔德（Otto Hölder）首次明确提出“分类所有有限单群”的构想。单群是数学中的“原子”——它们无法分解为更小的群结构，就像质数是数的基本构建块一样。赫尔德的开创性工作激发了早期研究者如伯恩赛德（Burnside）和科尔（Cole）的兴趣。伯恩赛德在1899年证明了第一个分类定理：若一个非阿贝尔单群的所有非单位元均为对合（阶为2的元素）或奇阶元素，则它必同构于 。这一阶段工具有限，主要依赖西罗定理和计数技巧。

20世纪早期：工具与初步探索

1900年左右，伯恩赛德和弗罗贝尼乌斯（Frobenius）利用新发展的群表示论（特征标理论）取得突破。伯恩赛德在1904年证明著名的 定理：阶为两素数幂的群必可解。弗罗贝尼乌斯则研究了弗罗贝尼乌斯群的结构。与此同时，美国数学家迪克森（Dickson）系统构造了有限域上的线性群，为后来的李型群分类奠定基础。这一时期的成果虽零散，但逐步建立了单群研究的框架。

1930-1950年代：理论奠基

德国学派（如费廷、维兰特、扎森豪斯）深化了群的结构理论。扎森豪斯在1937年的著作中强调“单群是构建所有有限群的砖石”，并提出了舒尔-扎森豪斯定理（关于群扩张的分解）。二战后，菲利普·霍尔（Philip Hall）发展了西罗定理的推广（霍尔子群），并证明“可解群等价于所有互素阶子群存在”。这些工作为后续分类提供了关键工具。

1950-1960年代：革命性突破

1963年，费特（Feit）和汤普森（Thompson）发表255页的《奇数阶定理》，证明“所有奇数阶群均可解”。这一里程碑不仅解决了伯恩赛德猜想，还引入了信号函子（signalizer functor）等新方法，将研究重心转向局部群论（即通过局部子群分析整体结构）。同期，布劳尔（Brauer）和铃木通夫（Suzuki）利用特征标理论刻画了某些单群的中心化子结构，而汤普森的学生时代成果（弗罗贝尼乌斯核的幂零性）成为后续工作的基石。

1960-1970年代： sporadic 群的爆发

随着分类进程加速，数学家们意外发现一系列“散在单群”（sporadic groups）——它们不属于已知的无限族（如交替群或李型群）。1965年，扬科（Janko）发现第一个散在群 ，随后费舍尔（Fischer）、格里斯（Griess）等人陆续构造出“魔群”（Monster，阶约 ）等怪物级结构。这一时期共发现26个散在群，其神秘性质（如“月光猜想”）至今仍是数学物理的研究热点。

1970-1980年代：最后的计划

戈伦斯坦（Gorenstein）在1972年提出16步分类纲领，将问题分解为“奇型群”和“偶型群”两大方向。阿施巴赫（Aschbacher）在1973年证明“标准分量定理”，极大简化了奇型群的分析。1980年，格里斯构造魔群的代数结构，标志散在群研究的收官。1981年，戈伦斯坦宣布分类基本完成，但“拟薄群”（quasithin groups）的细节直到2004年才由阿施巴赫和史密斯（Smith）补全。2004年，Aschbacher 和 Smith 发表 1200 页的论文，填补了最后的空白，正式完成分类。

现代影响与未解之谜

分类定理的最终形式断言：有限单群仅有四类——素数阶循环群、交替群、李型群和26个散在群。其证明跨越万页论文，汇集百位数学家的智慧。应用上，它解决了伯恩赛德受限问题（Zelmanov，1994），推动了表示论和几何的发展。但深层问题依然存在：为何散在群出现？是否存在更本质的“群起源理论”？正如汤普森所言：“我们仍在等待一位达尔文，用非林奈式的眼光统一这些硬核定理。”这一历程不仅是数学的胜利，更展现了人类合作与毅力的辉煌。从霍尔德的朴素提问到魔群的惊人构造，有限单群的故事仍在激发新一代的探索。

常见的有限单群

素数阶循环群

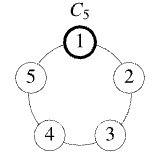
最简单的单群，其中 是素数。例如：（模5加法群）。

交错群 ​（）

由 个元素的偶置换构成。例如 （正二十面体的对称群），其阶数为 。

李型群（Lie-type groups）

这些群与线性代数、几何和有限域 密切相关。包括： 线性群如 （特殊射影线性群）。辛群如（保持辛形式的群）。例外李群如 ，其中 是某个素数的幂。

26个散在单群（Sporadic groups）

这些群不属于任何无限家族，而是孤立存在的例外。最大的散在单群是魔群（Monster group, ），其阶数约为 。其他著名的散在单群包括马蒂厄群（Mathieu groups）、康威群（Conway groups）等。

有限单群的分类是数学史上最雄心勃勃、最具挑战性的项目之一，也被誉为“数学的登月计划”。这一宏伟工程始于19世纪末，由数学家如Otto Hölder和William Burnside等人奠基，历经一个多世纪的努力，最终在21世纪初由Michael Aschbacher和Stephen Smith完成最后的证明。该项目集结了全球数百位顶尖数学家的智慧，总证明超过1万页，涉及深刻的群论、组合数学、几何和表示理论等领域的交叉融合这一里程碑式的成就不仅彻底解决了群论中最根本的结构问题，还为密码学、粒子物理、晶体学等应用科学提供了关键的理论工具。有限单群的分类是数学史上最庞大的工程之一，它不仅揭示了群的结构，还深刻影响了其他数学和物理领域。这一成就展示了数学的统一性和深度，至今仍是研究的热点。尽管分类已经完成，数学家们仍在继续简化证明、探索散在单群的深层性质，并寻找这些抽象结构在现实世界中的新应用。有限单群的分类不仅是纯粹数学的巅峰之作，更是人类理性思维追求统一与完美的永恒见证。