先说结论：复分析研究的是性质“最好的”函数，实分析研究的是性质”最差的“函数。

复分析与实分析是数学分析的两个重要分支，它们在研究对象、方法和性质上存在显著差异。

1. 研究对象

复分析：主要研究复变量的函数，即定义在复数域上的函数。复分析的核心对象是解析函数（全纯函数），这类函数在定义域内处处可微，并且满足柯西-黎曼方程（Cauchy-Riemann equations）。

实分析：研究实变量的函数，即定义在实数域上的函数。实分析的对象包括连续函数、可微函数、可积函数等，但更关注的是那些性质较差的函数，如处处连续但处处不可导的函数、狄利克雷函数（Dirichlet function）和康托尔函数（Cantor function）等。

2. 函数的性质

复分析：解析函数具有极强的正则性（regularity），例如： 解析函数在其定义域内无限可微。解析函数的局部性质可以完全决定其全局性质（如解析延拓）。解析函数的积分路径可以自由变形（柯西积分定理）。解析函数的实部和虚部是调和函数（满足拉普拉斯方程）。解析函数的零点孤立（除非函数恒为零）。

实分析： 实函数的性质更加多样化和复杂，例如： 存在处处连续但处处不可导的函数（如魏尔斯特拉斯函数）。存在可积但不可微的函数（如狄利克雷函数）。存在单调连续但导数几乎处处为零的函数（如康托尔函数）。实分析中的函数通常需要更精细的工具（如测度论、勒贝格积分）来研究其性质。可测函数”差不多“是连续函数。

3. 核心定理

复分析：

• 柯西积分定理（Cauchy’s Integral Theorem）：解析函数在简单闭合路径上的积分为零。
• 柯西积分公式（Cauchy’s Integral Formula）：解析函数的值可以通过其在边界上的积分表示。
• 留数定理（Residue Theorem）：计算解析函数在奇点处的积分。
• 最大模原理（Maximum Modulus Principle）：解析函数的模在边界上取得最大值。

实分析：

• 勒贝格积分（Lebesgue Integral）：比黎曼积分更一般的积分理论，适用于更广泛的函数类。
• 单调收敛定理（Monotone Convergence Theorem）：单调递增的非负可测函数序列的积分与极限可交换。
• 控制收敛定理（Dominated Convergence Theorem）：在控制函数的条件下，极限与积分可交换。
• 鲁津定理（Luzin’s Theorem）：几乎处处有限的函数在适当条件下可以“几乎连续”。

4. 应用领域

复分析： 在物理学中用于研究流体力学、电磁学和量子力学，在工程学中用于信号处理和控制系统，在数论中用于研究素数分布（如黎曼 zeta 函数），在复动力系统中研究分形结构。个人感觉复分析的发展依赖于解析数论的那些大问题。

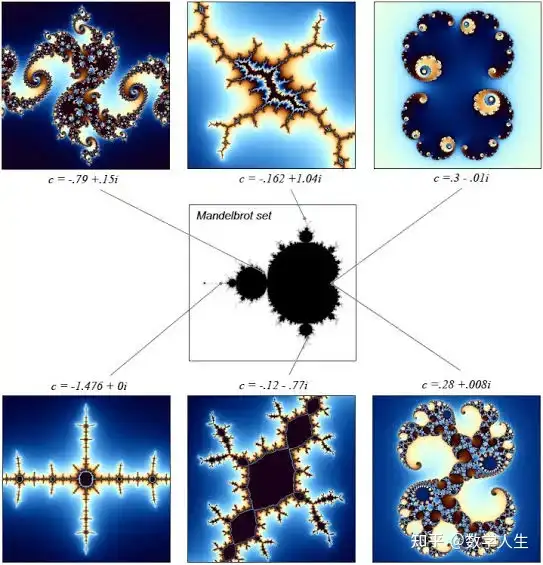
实分析： 在概率论中用于研究随机过程和测度论，在动力系统中研究遍历理论，在经济学中用于优化理论和博弈论。

5. 总结

复分析和实分析虽然在形式上都是研究函数的性质，但复分析更关注那些性质极好的函数（解析函数），而实分析则更关注那些性质复杂甚至“病态”的函数。复分析的许多结果依赖于复数的特殊性质，而实分析则需要更一般的工具（如测度论）来处理实函数的多样性。两者在数学和应用科学中都有广泛的应用，并且相互补充，共同构成了现代分析学的基础。