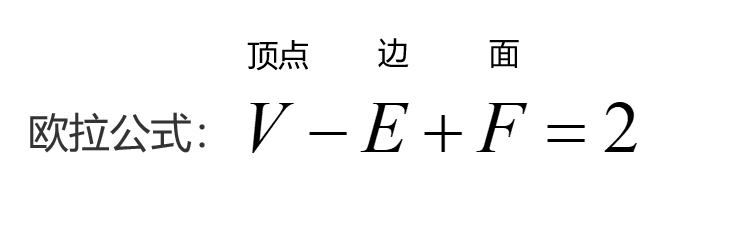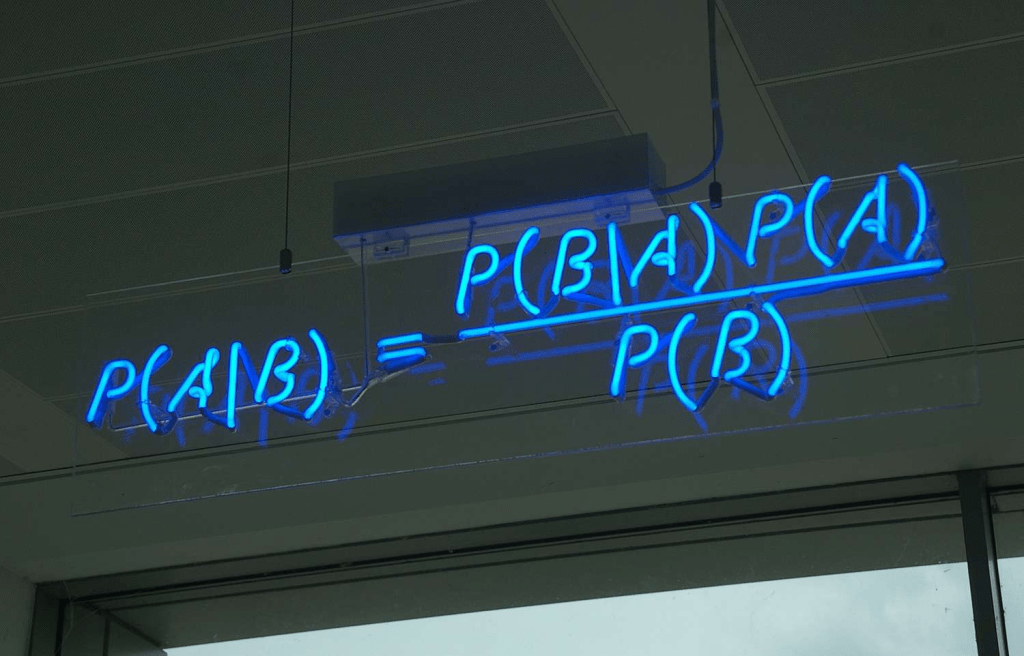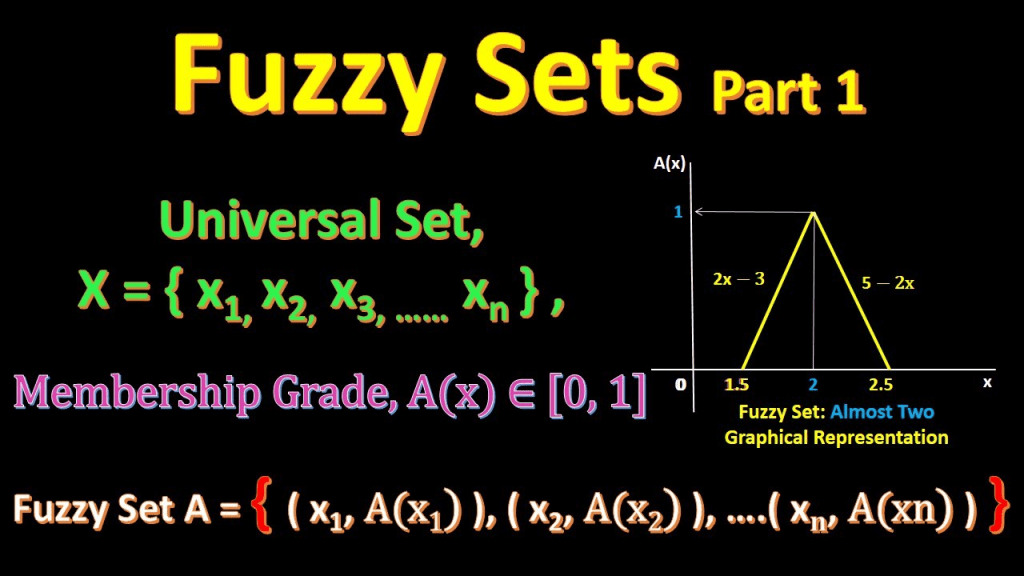在极远极远的过去,数学界的世界一片璀璨,几座神奇的城池横亘在这片土地上。首先是“算数丘城”,那里住着微分方王、积分方伯、变换方公和几何王子。他们的城池,虽然有时风景如画,却总是布满了各种极限、收敛与发散的迷雾。然后是“群体之城”,它有一个独特的结构,既有哈密顿广场、概率城、又有李群大道;每一条路都被不等式区隔开来,深藏着许多离散与连续的深奥谜题。
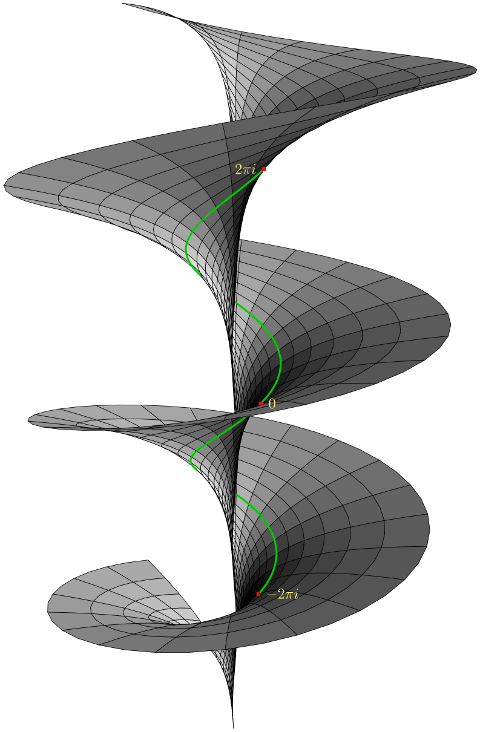
在这些城池间,有一条河流叫做“代数溪”,河水清澈见底,充满了各种群的原型,有时流得急促,有时又变得缓慢。每年都有不计其数的流派聚集在这条河边,讨论群的性质、环的结构、域的扩展与代数方程的解法。这里的村民过着不平凡的生活,他们的名字或许听上去十分熟悉,却隐藏着无穷的数学智慧。村头有一个老教授,名叫“高斯”,他以开拓尺规作图正十七边形、无穷大和无穷小的疆域而闻名。人们常听到他传授在“复数村”创造的奇迹,讲述那些关于欧拉公式和复变函数的故事。他的居所是一座古老的塔楼,塔楼上刻着不朽的名句:“真理总是深藏在解的边缘”。高斯的朋友,黎曼,也常常出现在塔楼里,二人就黎曼猜想、黎曼曲面、以及曲率问题热烈争辩。每当他们辩论激烈,塔楼外的风会变得狂乱,仿佛在回荡着无数未解的数学疑问。
再往北行,便是“概率城”,在这座城市里住着伯努利兄弟、拉普拉斯和伯努利兄弟。这里有一条名为“标准正态分布河”的河流,水流宽广,急速湍流。每天清晨,贝叶斯与费马都会围绕着先验概率与后验概率进行激烈的争辩,哪怕只是为了讨论一小块概率密度的形状。这个城市的特色之一是人们常穿着拉普拉斯设计的“概率服”,那种衣服不仅能让人隐形,还能隐藏所有的不确定性。还有柯尔莫哥洛夫(Kolmogorov)这位数学家,将概率论进行公理化,让大家都围绕着这个体系运作。
在“算数丘城”与“概率城”的交界处,坐落着一座神秘的“映射宫殿”。这座宫殿的结构极为复杂,每一层都通过不同的映射连接。映射宫殿的主人是一个著名的数学家,他的名字叫做“康托尔”(Cantor)。他以研究“集合论”和“无穷”而著名,在他的宫殿中,所有的物体、事件和空间都可以通过不同的映射被彼此联系。每一扇门、每一根柱子、甚至每一根绳索,都与“康托尔集”上的点有着某种微妙的对应关系。宫殿的屋顶是无穷的分形图案,时刻在变化,时而显现出细致的维数,时而展现出无限的自相似。
在康托尔的宫殿深处,有一个大大的“基尔伯特空间”,这是一个神秘的地方,拥有着极高的数学价值。基尔伯特空间里没有传统意义上的点,只有数不清的“向量”和“超函数”。这里的每一件物品都是一个函数,每一条线段都是一个向量,甚至连空气中的气流也是由无穷多个谱系的正交基所组成。在这里,赫尔曼·闵可夫斯基(Minkowski)和特奥多尔·冯·纽曼(Von Neumann)正在密切合作,他们探索着量子力学与数学结构的奥秘,甚至深入到数学与物理的交汇点,讨论着如何通过线性代数与算子理论来描述量子态的变换。
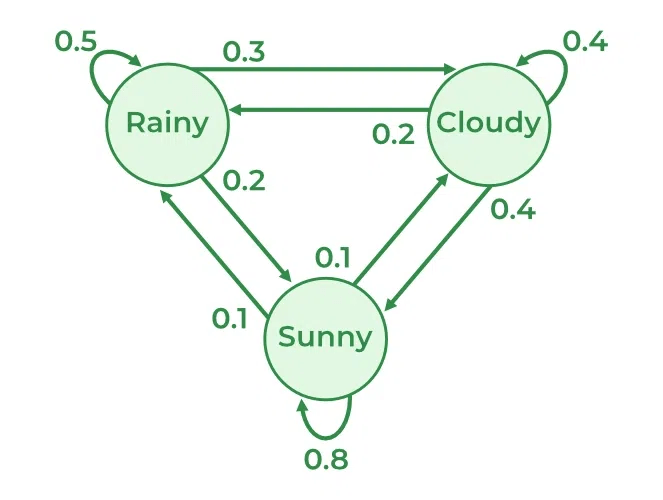
映射宫殿的周围有一片神秘的“拉普拉斯湖”,湖水清澈见底,但却流动着无尽的概率波动。每当月光照耀在湖面上时,波动的几率与函数就会以极其奇异的方式交织成美丽的图案,仿佛是某种奇异的统计分布。湖边常有一位老者坐在岩石上冥思,他就是“马尔科夫”(Markov)。他身着“随机过程长袍”,时而低声自语,时而向前方的极限倾诉。马尔科夫的最大贡献是“马尔科夫链”理论,这也是他在随机过程领域的独到之处。人们经常听到他谈论“平稳过程”、“独立增量”,以及如何运用“马尔科夫不等式”预测未来的随机事件。
在“几何山谷”,几何大师欧几里得、阿基米德、高斯的几何派弟子、黎曼和罗巴切夫斯基的弟子聚集在一起,讨论着平面几何与空间几何的奇妙图形。这个地方藏着一座几何宝塔,塔上有一行古老的铭文:“所有直线都汇聚在无穷远处。”这座塔的周围有一个神秘的区域,叫做“李群园”,园内的树木都是由群论构成,每一棵树都有一个独特的群表示,群木的枝繁叶茂像极了复杂的群结构。
在“微积分之海”,牛顿和莱布尼茨常常一同乘船,遨游在无穷小的浪花之间。他们的讨论内容永远不离求导与积分的美妙,有时他们也会偶尔停下来,向他们的同伴,欧拉、达朗贝尔与拉格朗日展示他们为数不多的数学成果。微积分的每一个波动都充满了创造与启发,仿佛数的精灵在海面上自由舞动。
继续往南,穿越“积分荒原”,你会遇到一座座如同“黎曼几何”的“石塔”,这些石塔中藏着一位又一位著名的数学家。这里有“菲尔兹”塔、还有“赫尔德”塔,它们的顶端都镶嵌着用“拉普拉斯变换”雕刻的精美图案,标志着这些伟大数学家的无穷探索和成就。而塔下,总有学者在进行“拉格朗日乘数法”和“柯西-施瓦茨不等式”的比试,看谁能在复杂的条件下,找到最优的极值。
再往东,远远的“拓扑村”伫立在群山之中。在这里,庞加莱总是与拉克莱布和斯图尔特一同,探讨拓扑空间与同调理论,探讨扭结、缠绕、孔洞与映射之间的千丝万缕的关系。这里的树是由不连续的空间组成,根部在无限小的空间中能看到“李群”的影子。每当这些拓扑学者散步时,脚下的道路会变形、拉伸,仿佛在展现那些神秘的同伦群。在“拓扑村”的深处,有一个叫做“类比道”的地方,专门用来讨论“同伦”和“同调”的问题。这里的居民是一些专门研究“拓扑空间”的学者,他们常常在村庄里讨论“连通性”、“紧性”以及“欧拉示性数”。每年的秋天,这里会举行一场盛大的“同调竞赛”,数学家们需要借助“霍普夫映射”和“阿特伍德定理”将不同的拓扑结构归约到一个标准化的模型。赛场上,选手们展示了他们的“拓扑不变量”,各种“嵌入定理”与“同调群”在空中飞舞,仿佛能触碰到天空的极限。
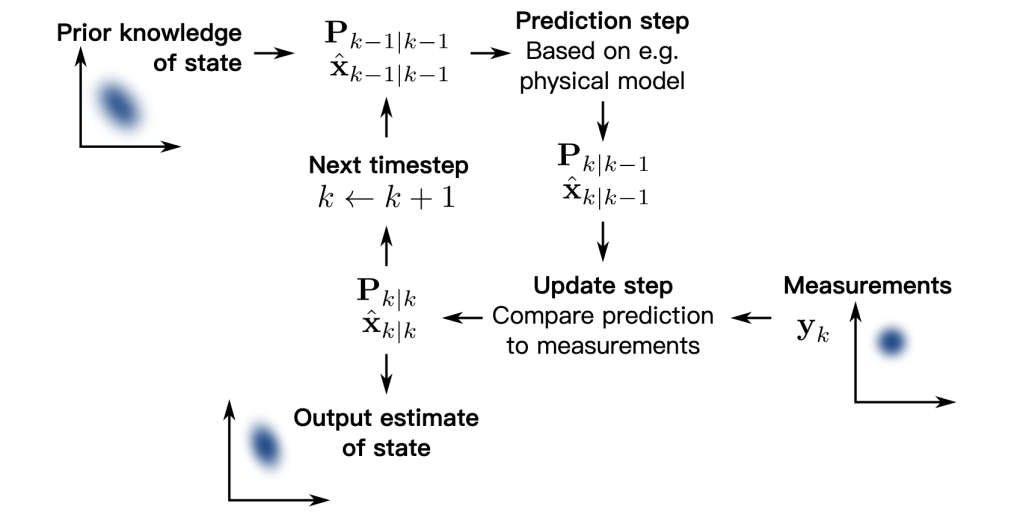
而在“微分方程之峡谷”中,常常传来阵阵高亢的讨论声。这里的住民是一群钟情于微分方程的学者,最著名的当属“欧拉-拉格朗日”二人组。欧拉总是在研究如何用“常微分方程”来刻画物理现象,而拉格朗日则致力于通过“变分法”来发现最优解。在这片峡谷中,人们有时还会见到一位“卡尔曼”大师,他带着一只神奇的“卡尔曼滤波器”,总能在复杂的动态系统中,提取出最重要的“状态估计”。每当卡尔曼大师走进峡谷,附近的树木、河流、甚至空气中的噪声都会开始静默,仿佛都在等待着他对“最优控制理论”的深刻解答。
在“度量空间山脉”的另一端,有一片“概率森林”。这片森林有着独特的规律,任何一棵树的生长都遵循“泊松过程”,森林的土壤中充满了“不确定性”,每一片叶子都是一个随机变量。森林的深处藏着“贝叶斯-帕松-拉普拉斯”三位贤者,他们经常在这里探讨如何通过“贝叶斯网络”来建构统计模型,或者如何通过“极大似然估计”来预测未来的事件。
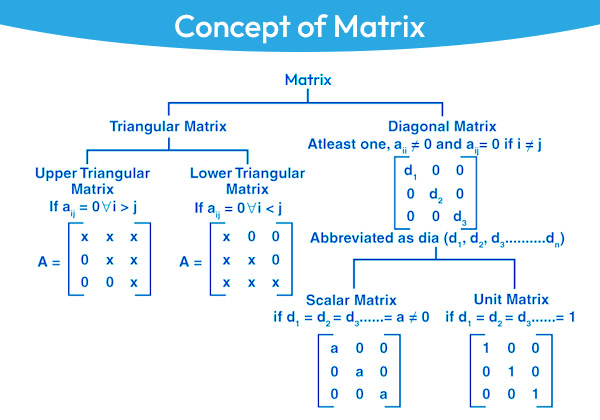
在“矢量空间平原”上,众多数学家们像欧几里得、阿基米德、笛卡尔等,都在这片广袤的平原上留下了他们的足迹。在这片广阔的领域内,“线性代数”的大师总是带着他的“矩阵”与“特征值”,在不断地将不同维度的空间互相转换,创造着极限与无限之间的美丽画卷。除此之外,还有一片广袤的“希尔伯特平原”,平原上生长着众多的数学森林和神秘的定理山脉。其中有一条通往“范畴之城”的道路,这条路是由“范畴论”铺设的,它用一条“同构”桥连接着不同的数学领域。这个城市的建设者是“埃尔朗”(Eilenberg)和“马尔基厄尔”(Mac Lane),他们共同创造了“范畴论”的基础,强调了数学结构间的关系与变换。每当人们走进范畴之城,都会看到“函子桥”和“自然变换塔”巍然矗立,仿佛在讲述一个个不同领域之间的“同伦”与“同调”的深刻联系。
在城市的北部,有一片被称为“模糊逻辑草原”的广袤区域。这里住着“扎德”(Zadeh),他是“模糊集合”理论的奠基人。这片草原的特殊之处在于,任何物体的边界都变得模糊不清,定义变得不再是明确的零和一。在这里,“模糊集合”和“隶属度函数”像是草原上飘动的风,能够让不确定性和模糊性在数学中得到应用。
再往东,进入了一个被称为“数值分析岛”的地方,岛上遍布着“高斯-赛德尔迭代法”和“雅可比法”的魔法阵。岛屿的中心有一座神秘的“数值逼近塔”,塔内住着和“库塔”(Martin Kutta),他们经常在塔内探讨“数值解法”和“误差分析”。塔顶悬挂着一块“收敛性”铭文,表明只有那些能在有限步骤内求得近似解的算法,才配得上进入塔顶。

岛屿的西面,有一座高耸的“图论山”,山顶处矗立着欧拉(Euller)和其他数学家,他们共同建立了图论的经典理论,推动了“图的着色”和“图的遍历”这两项基础理论的诞生。这里的居民时常以“图的连通性”与“欧拉回路”讨论,时而利用“斯图尔特定理”来指导他们如何在复杂网络中找到最佳路径。在岛屿的南方,是一片充满数理逻辑和不确定性的“哥德尔沼泽”,这个地方的主人是“哥德尔”(Gödel),他以其“不可判定性”定理著称。哥德尔沼泽中的水面时常漂浮着一些“自指”与“递归”的奇怪生物,它们不停地在“数理模型”中穿梭,试图破译“形式系统”的奥秘。这里的空气充满了“逻辑推理”的味道,每当春风吹过时,就会出现一阵“哥德尔不完全性”的阵阵回响。
南方不远,有一座叫做“拓扑荒野”的地方,荒野中住着斯坦因(Steenrod)与塞尔(Serre)。他们探索了拓扑学的边界,在此建立了“同调理论”和“层理论”。拓扑荒野的地形总是令人迷惑,时而平坦如“霍普夫环面”,时而曲折如“克莱因瓶”。这里的每一块岩石、每一棵树、每一滴水都充满了“连续性”和“同胚”的特性,仿佛能在无限的变换中保持不变。
而在“统计王国”的深处,住着“费舍尔”(Fisher)、“诺伊曼”(Neumann)与“皮尔逊”(Pearson)三位巨匠,他们共同开创了“统计推断”的新时代。在这里,密布的“概率密度森林”和“回归分析草原”里,弥漫着“不确定性”的气息。居民们时常在“极大似然估计”与“最小二乘法”的指引下,走向真理的彼岸。每当“费舍尔方差分析”传出声音时,周围的“抽样”与“假设检验”便会随着算法的变化而起伏。
在这片充满智慧和奥秘的“数学大地”上,有一座神秘的“计算机科学宫殿”。这座宫殿的建设者是“图灵”(Turing),他不仅是“图灵机”理论的创始人,还揭示了计算和可计算性的极限。宫殿的中心是一个巨大的“图灵测试”大厅,里面时常有来自各个领域的数学家和工程师在测试人工智能的极限,进行着一场场关于“算法复杂性”和“计算模型”的深刻对话。
计算机科学宫殿的周围有一片“信息论森林”,在这片森林中,“香农”(Shannon)和“哈夫曼”(Huffman)时常聚集在一起,讨论信息的“压缩”与“编码”问题。每当他们挥动手中的“信息熵公式”时,森林中的鸟儿似乎也开始发出更具“信息量”的鸣叫,仿佛在向世界传递着知识的真谛。
在“数学帝国”的东南角,有一片被称为“动力系统之海”的地方,那里充满了涌动的波涛与湍流。这里的领主是“庞加莱”(Poincaré),他是混沌理论的奠基人之一。在这片海洋中,任何一个小小的扰动都会引发系统的剧变,仿佛在传达着“初始条件敏感性”的深刻道理。海面上漂浮着“李雅普诺夫指数”的符号,预示着“稳定性”与“不稳定性”之间的永恒博弈。沙滩上存放着“斯梅尔马蹄”,象征着稳定的系统也会带来混沌。
在复数的世界里中,存在着两位伟大的数学探险家——Fatou与Julia。他们穿越了复数平面的神秘荒原,创造了复动力系统的基石。他们通过不懈的研究,发现了在复平面上,某些函数的迭代过程会演化出令人惊异的图形。Fatou专注于研究这些迭代过程的稳定性,而Julia则深入探索了这些过程的边界行为。他们的工作奠定了复动力学的基础,揭示了复数上“吸引域”和“逃逸域”之间复杂而美丽的关系。尽管他们的发现曾一度被忽视,但他们留下的理论为后来者铺设了通往深奥几何的道路。五十年后,一位名叫Mandelbrot的数学家,他仰望着复数平面的星空,发现了更加神秘的景象。他用无穷迭代的技术,揭示了一个无穷小的区域,这个区域的边界既不规则又精美,像是自相似的图案重复展开。这就是分形的起源,Mandelbrot集——一个既简单又极为复杂的图形,它的边界充满了无穷的细节。每次放大,它都展现出崭新的世界,如同数学世界的无尽宇宙,充满着无尽的可能性与奇迹。与此同时,Dennis Sullivan站在前人发现的基础上,揭开了一个新的谜题。他用极其精细的拓扑手段,证明了一个深刻的命题——有理函数没有游荡区间。他向世人展示了复数上的拓扑结构的力量,证明了无论多么复杂的函数,在适当的条件下都必须遵循某种精确的秩序。Sullivan的工作为动力系统带来了新的光辉,揭示了在混沌的世界中,依然隐藏着无法逃脱的内在秩序。
这些地方和人物共同构成了21世纪前的数学风景画,承载着数不尽的定理、公式与想法,像一条条交织的河流,永远流向未知的远方。此时此刻,四方的数学巨匠与神秘的数学力量共同演绎着世界的奇妙构造,无论是微分方程的华丽舞步,还是拓扑空间的神秘网格,亦或是代数群的无穷回响,都在这片土地上勾画出数学无穷尽的美丽与奥秘。
备注:
- 高斯 (Gauss) – 德国数学家,贡献包括数论、概率论、复变函数等。
- 黎曼 (Riemann) – 德国数学家,以研究复变函数和几何方面的贡献著称,尤其是黎曼猜想。
- 伯努利兄弟 (Bernoulli) – 瑞士数学家家族,主要贡献在概率论和流体力学等领域。
- 拉普拉斯 (Laplace) – 法国数学家、天文学家,贡献包括天体力学、概率论。
- 欧几里得 (Euclid) – 古希腊数学家,被誉为几何学的奠基人。
- 庞加莱 (Poincaré) – 法国数学家、物理学家,拓扑学的奠基人之一。
- 牛顿 (Newton) – 英国数学家、物理学家,微积分的创始人之一。
- 莱布尼茨 (Leibniz) – 德国哲学家、数学家,微积分的共同发明者之一。
- 康托尔 (Cantor) – 德国数学家,集合论的创始人之一,提出了不同大小的无穷集合。
- 马尔科夫 (Markov) – 数学家,特别是马尔科夫过程的研究者,马尔科夫链理论的重要人物。
- 卡尔曼 (Kalman) – 美国数学家,卡尔曼滤波器的发明者,广泛应用于控制理论与信号处理。
- 黎曼几何 (Riemannian Geometry) – 由黎曼创立的一种几何学,研究曲面和流形的性质。
- 柯西-施瓦茨不等式 (Cauchy-Schwarz Inequality) – 数学中著名的不等式,涉及向量的内积空间。
- 范畴论 (Category Theory) – 由埃尔朗和马尔基厄尔发展,强调对象和态射之间的关系。
- 模糊集合 (Fuzzy Set) – 扎德提出的集合理论,允许元素具有模糊的隶属度。
- 高斯-赛德尔迭代法 (Gauss-Seidel Iteration) – 数值分析中的迭代方法。
- 图论 (Graph Theory) – 研究图形结构的数学分支。
- 哥德尔不完全性 (Gödel Incompleteness) – 哥德尔提出的定理,表明任何足够强大的数学系统都存在不可判定的命题。
- 极大似然估计 (Maximum Likelihood Estimation) – 一种估计参数的方法,常用于统计推断。
- 图灵机 (Turing Machine) – 图灵提出的计算模型,是理论计算机科学的基础。