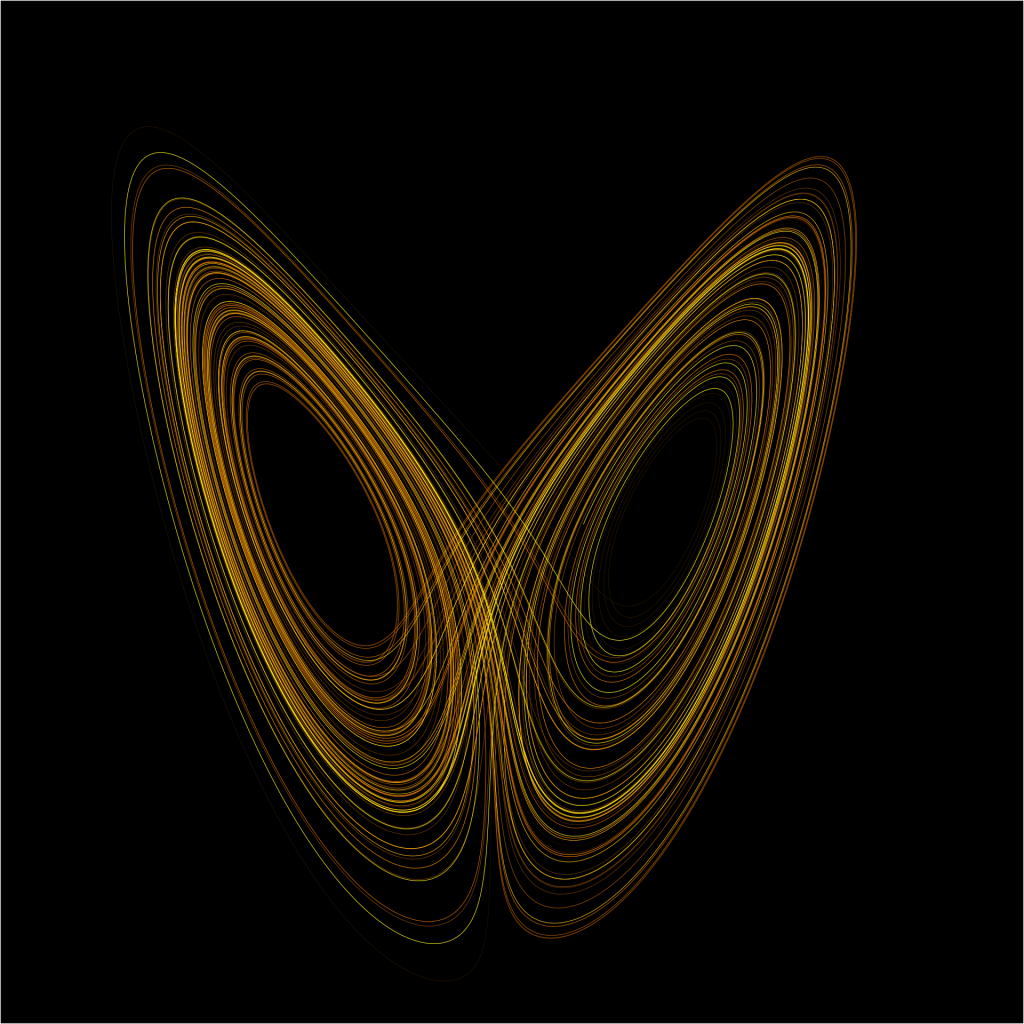斯蒂芬·斯梅尔（Stephen Smale）是20世纪和21世纪最具影响力的数学家之一。他的学术生涯横跨拓扑学、动力系统、数学经济学以及计算理论等多个领域，留下了一系列深刻而广泛的贡献。1930年7月15日出生于美国密歇根州的弗林特市，前几天便是他的 95 岁大寿。斯梅尔在密歇根大学完成了他的本科与博士教育，他的博士论文题为《黎曼流形上的正则曲线》，导师是著名数学家劳尔·博特（Raoul Bott）。然而，这位年轻数学家的真正声名鹊起，源于他1961年完成的一项震惊世界的突破：高维庞加莱猜想的证明。

庞加莱猜想被认为是20世纪最重要的数学难题之一，其本意是探究在高维空间中，若一个光滑流形与球面具有相同的基本拓扑性质（即同伦等价），它是否必定就是球面本身（在同胚意义下）。斯梅尔巧妙地结合莫尔斯理论和他开创的h-配边定理（h-cobordism theorem），成功证明了当维度大于等于5时，这一猜想成立。这项工作不仅解决了一个长久未解的拓扑难题，更为后来维度较低情况下（尤其是三维庞加莱猜想）的问题奠定了理论框架和方法论基础。凭借这一成果，斯梅尔获得了1966年菲尔兹奖——这是数学界的最高荣誉之一。

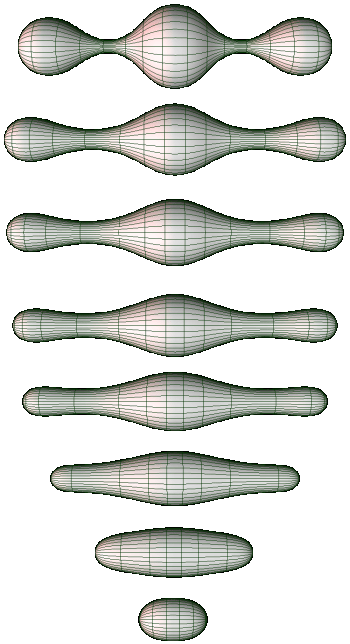
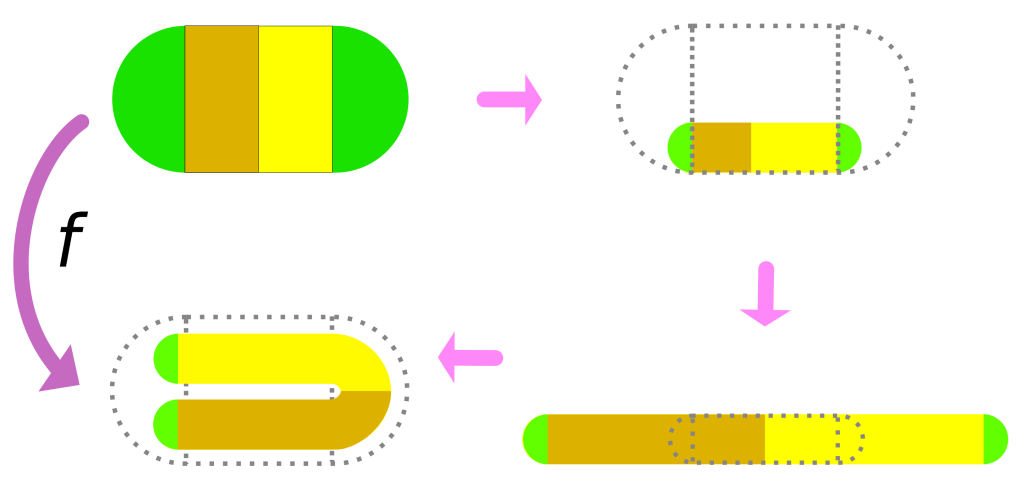
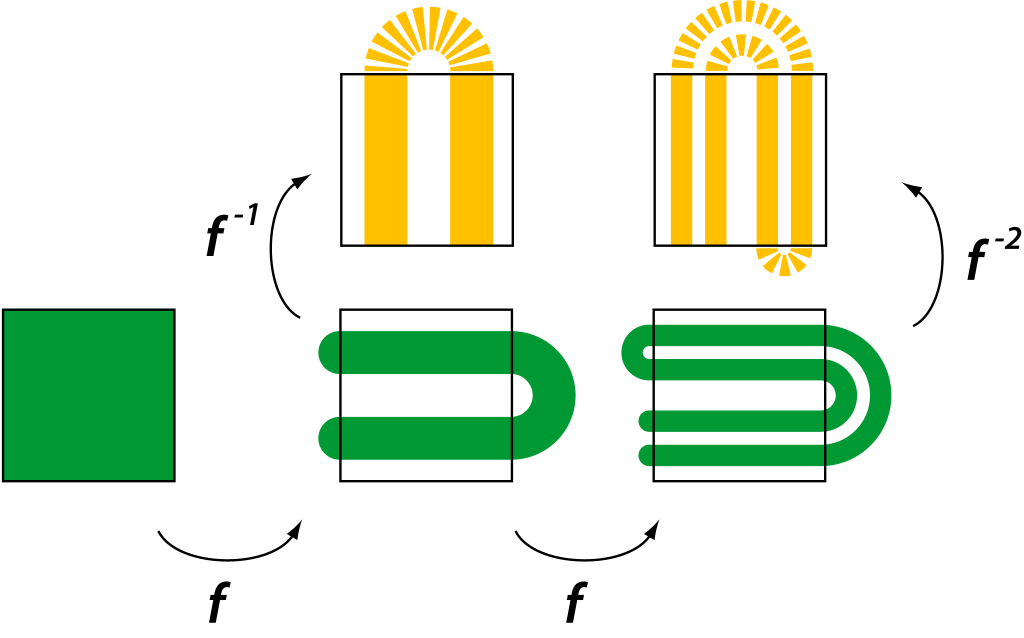
然而，斯梅尔的视野远不止于拓扑学。他在动力系统理论中的工作同样具有革命性意义。最为人所津津乐道的是“斯梅尔马蹄映射”的提出。这个模型起源于他在巴西里约热内卢海滩度假时的灵感，被他戏称为“我最好的数学不是在办公室里完成的，而是在海滩上诞生的”。马蹄映射的几何图像非常直观：它将一个正方形区域拉伸、折叠，形成马蹄形状，再将其重新放回原始空间。这个简单的变换却产生了惊人的后果——在迭代中，它展示出对初始条件的极度敏感，导致轨道呈指数级分离，这正是“混沌”现象的核心特征。

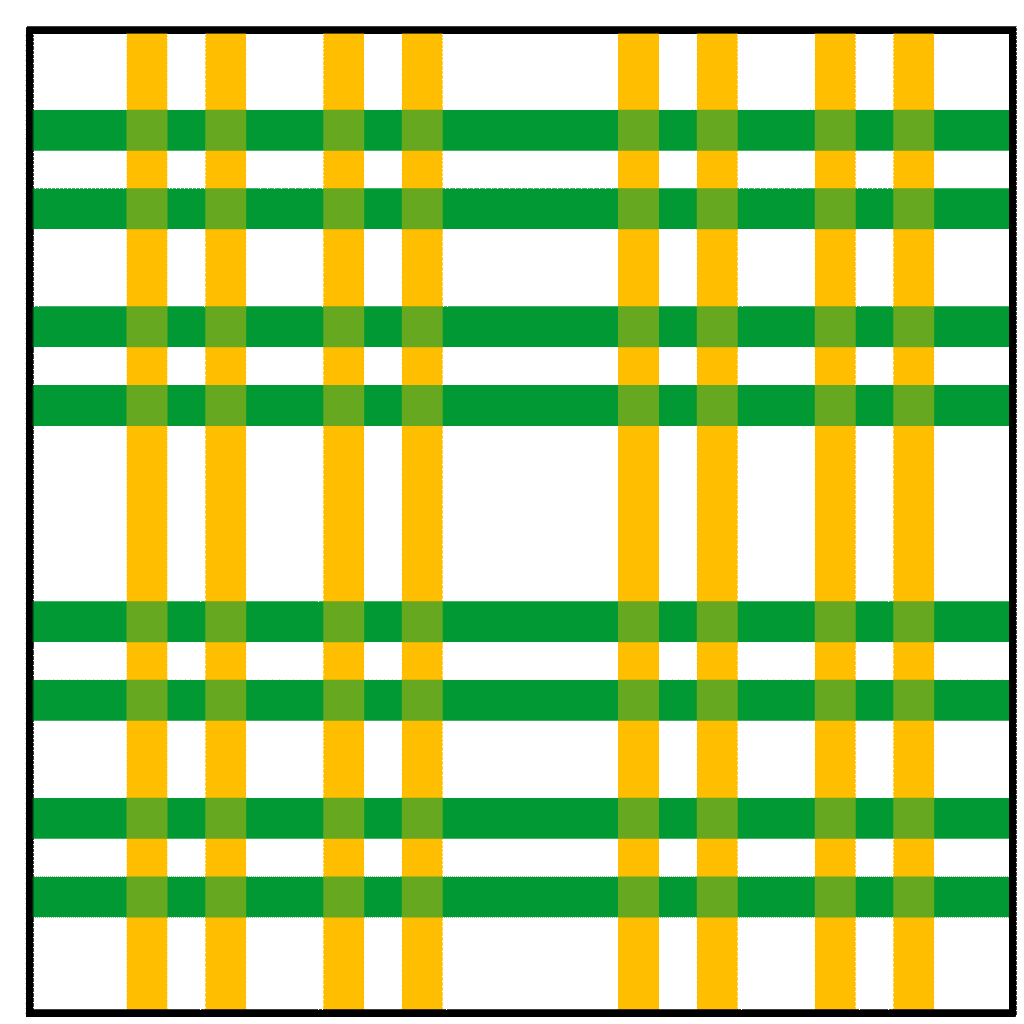
通过对马蹄映射的严格数学分析，斯梅尔首次为“混沌”这一广义概念赋予了明晰而严密的定义。他证明该映射在一个康托集（Cantor set）上存在一个双曲不变子集，其动力学行为等价于伯努利移位这类符号动力系统。这意味着，即便一个系统在每一步的演化规则完全确定，其长期行为也可能表现出无法预测的复杂性。斯梅尔由此揭示出一个深刻的真理：在完全确定性的世界中，也潜藏着无限复杂与不确定性。

在进一步研究中，斯梅尔发展出莫尔斯-斯梅尔系统（Morse-Smale systems），这是一类结构稳定的动力系统，具有明确的吸引子与排斥子结构。他将莫尔斯理论与动力系统结合起来，构建了一套分析系统稳定性与拓扑结构之间联系的工具体系。在这些系统中，轨道的行为可以通过有限个稳定和不稳定的周期点来描述，从而使得对其长期演化的分析成为可能。这些理论成果不仅对数学内部产生了巨大影响，也为物理学中的湍流、气象学中的气候模型、工程中的非线性控制系统等提供了核心框架。

斯梅尔的视角一向超越数学的分科壁垒。他认为数学的真正魅力在于其结构性的思维方式可以应用到其他复杂系统中。1990年代以来，他开始关注经济学和计算理论，并与Shub、Blum合作提出了Blum–Shub–Smale模型（BSS模型）。这一模型旨在将传统图灵机的离散计算框架推广到实数域，建立一个能够处理连续变量问题的复杂性理论基础。这个模型尤其在研究数值计算复杂度、优化问题的可解性等方面，提供了重要的理论支持。

他还将拓扑工具引入经济学研究，试图用几何与动力系统的方法理解市场均衡的存在性与稳定性。例如，在研究一般均衡理论时，他探讨了价格调整过程是否能够收敛到均衡点，从而为新古典经济学中的“看不见的手”提供了数学分析的可能性。这种跨学科的工作风格，使斯梅尔在多个学科领域都留下了不可忽视的印记。

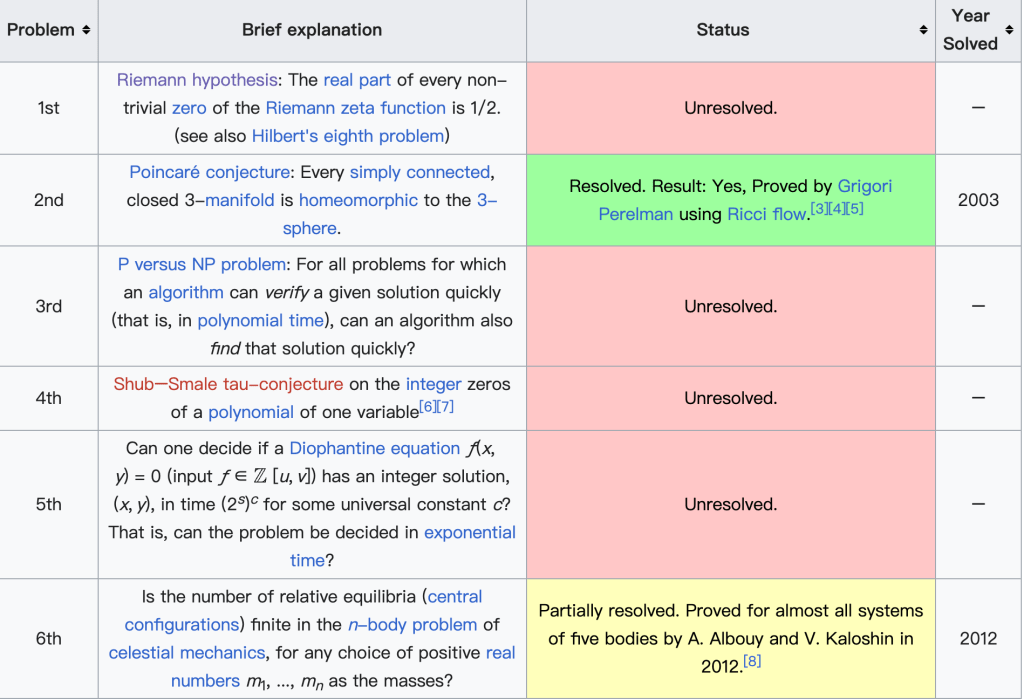
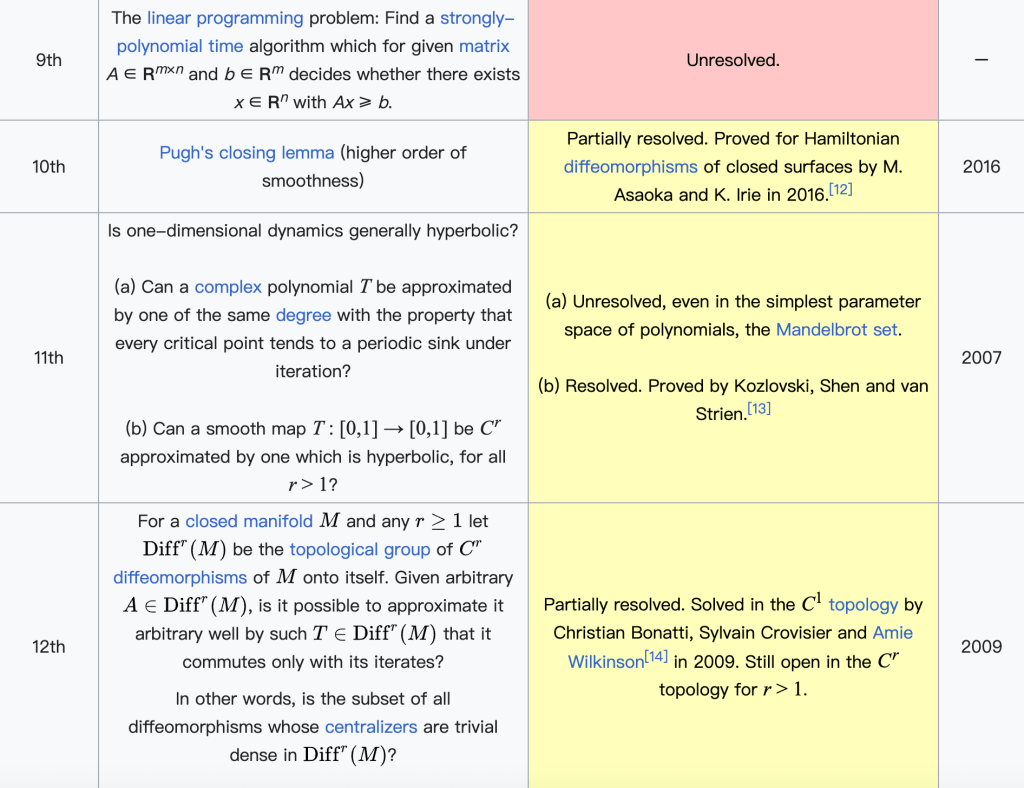
在斯梅尔看来，数学的发展不仅依赖于过去问题的解决，也需要对未来的大胆构想。1998年，他仿效大数学家希尔伯特的传统，发布了21世纪数学问题清单，总共列出18个未解的重要问题。这些问题涵盖数论、代数几何、计算理论、偏微分方程与动力系统等多个前沿方向。其中包括著名的黎曼猜想、P vs NP问题、纳维–斯托克斯方程的解的存在性与光滑性等，这些问题后来也被选为千禧年七大数学难题的一部分。斯梅尔的问题清单不仅展示了他对数学整体脉络的深刻理解，也对21世纪的数学研究方向产生了重要影响。

作为一位导师，斯梅尔同样具有极强的影响力。他培养的48位博士生中，有许多成为动力系统和混沌理论的领军人物，其中包括与他合著《微分方程、动力系统与混沌导论》的莫里斯·赫希（Morris Hirsch）和著名的科普作家、混沌研究者罗伯特·德瓦尼（Robert L. Devaney）。他们共同撰写的这本教材，已被引用超过12,000次，成为全球无数数学系与工程系课程的标准读物。

斯梅尔的学术成果受到世界广泛认可，除菲尔兹奖外，他还获得了美国国家科学奖章（1996）、沃尔夫数学奖（2007）、奥斯瓦尔德·维布伦几何奖（1966）和肖维内奖（1988）等诸多荣誉。他的影响甚至延伸至天文学界，一颗小行星被命名为“斯梅尔行星”（Smale Planet），以纪念他对科学的贡献。

斯梅尔一生坚持以非传统的方式思考问题，他喜欢说：“我的最佳数学灵感，往往不是在办公室里获得的。”这一观点在他创造马蹄映射的经历中得到了最好的诠释。他的经历证明了自由的思维环境与非线性的灵感源泉，往往比传统学术模式更能激发创造力。

斯梅尔的动力系统理论阐释了一个核心思想：简单规则可以孕育无限复杂。从高维拓扑到混沌动力系统，从实数计算理论到经济系统的动态建模，他持续推动数学扩展其疆域，直指自然与人类社会中深层的秩序与混乱。他让我们看到，在最基础的规则中，藏着宇宙运行的密码，而数学，正是我们用以破译这密码的语言。