百年数学难题的终极突破：Kakeya猜想的三维解答

在数学的浩瀚宇宙中，许多看似简单的问题背后都暗藏玄机，令人琢磨不透。1917年，日本数学家挂谷宗一（Soichi Kakeya）提出的一个几何问题，乍看之下或许不以为意，但却开启了一个跨越百年的数学探索之旅。问题的核心是：“在平面上旋转一根单位长度的针，所需的最小面积是多少？”这个问题，后来被称为挂谷转针问题（Kakeya needle problem），而它背后的挑战则是现代几何测度论中的一个深刻谜题——挂谷猜想（Kakeya conjecture）。

 从旋转针尖到数学革命

经典答案的颠覆

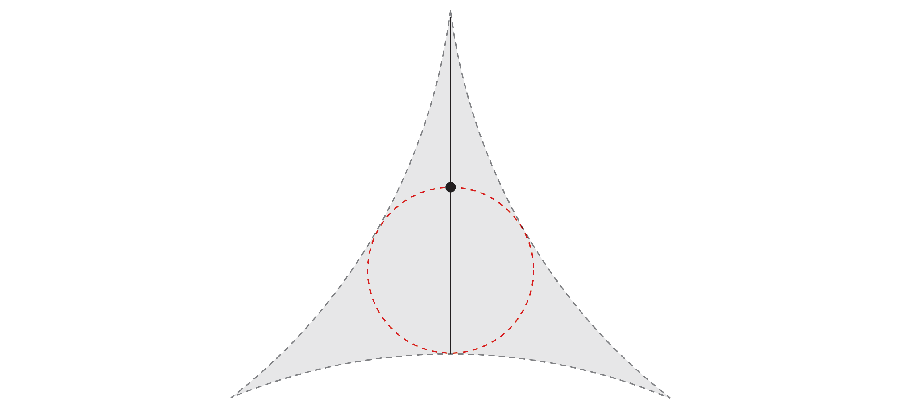
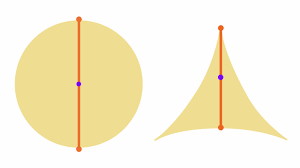
初期，数学家们认为，最小面积应由等边三角形（面积约0.577）或三尖点内摆线（面积0.392）实现。然而，在1928年，俄裔数学家贝西科维奇（Abram Besicovitch）提出了令人震惊的构造，证明了存在一种名为“贝西科维奇集”（Besicovitch set）的几何形状，它能够在几乎任意小的面积内容纳所有方向的单位线段。这个看似反直觉的结论的核心是“帕尔连接”（Pal join）技巧，通过平移和重叠三角形切片，极限压缩面积至几乎为零。

维度之谜的浮现

随着时间的推移，数学家的目光从面积转向了维度的谜题。1971年，罗伊·戴维斯（Roy Davies）证明了二维空间中的贝西科维奇集的豪斯多夫维度必须为2，意味着在平面上，包含所有方向单位线段的集合必须填满整个平面。然而，问题在三维空间中变得更加复杂。挂谷猜想的核心命题问的是：如果一个集合包含所有方向的单位线段，那么在三维空间中，它的维度是否必然为3？这个问题困扰了世界顶尖数学家近50年，甚至包括陶哲轩等人。

三维突破：王虹与Zahl的世纪性证明

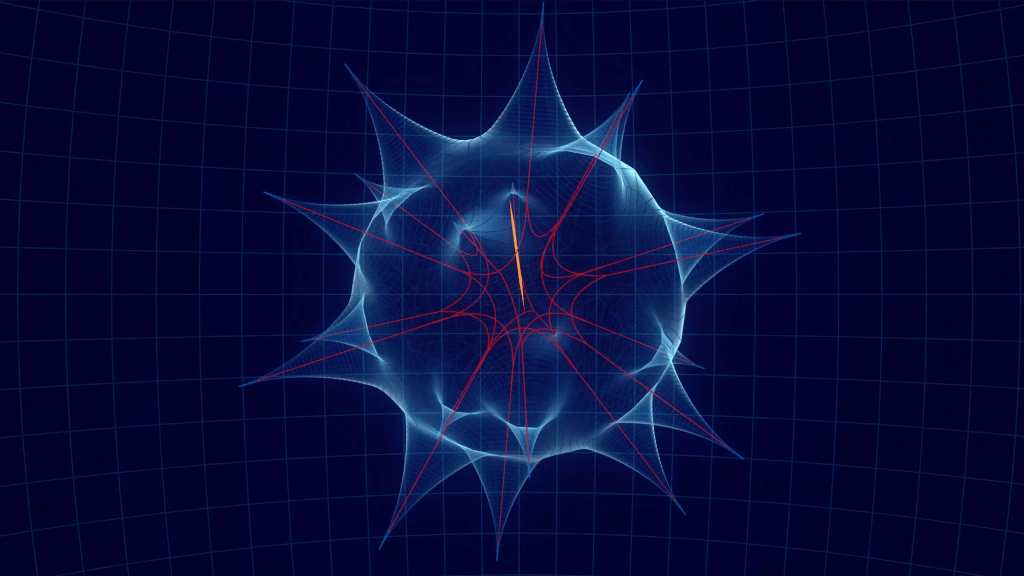
终于，2025年2月，纽约大学的王虹和英属哥伦比亚大学的Joshua Zahl发布了一篇128页的预印本论文，彻底解决了三维挂谷猜想的问题。

定理：三维空间中的任何挂谷集，其豪斯多夫维数与闵可夫斯基维数均为3。

这意味着，无论如何精巧构造，三维空间中“容纳所有方向线段的集合”必须占据满维空间，无法被无限压缩。这个突破性的结果被誉为“世纪性成果”，解决了几何测度论中的核心难题，并为相关数学领域提供了新的思路。

证明的核心创新

粘性集合（Sticky Kakeya sets）：

王虹与Zahl的研究首先集中在一个全新的概念上——粘性集合。他们提出，如果挂谷集在多个尺度上展现出“自相似粘性”（即细管高度聚集于粗管），那么其维度必为3。这一发现成为解决问题的关键之一。

多尺度归纳法：

在研究过程中，王虹与Zahl通过递归分析不同尺度下管状结构的“密度阈值”，成功将非粘性情况转化为粘性框架，最终得出了正确的结论。他们的研究突破了传统方法的限制，运用了代数几何与组合技术，尤其是多项式方法和投影几何技术，有效突破了过去几十年数学家的思维束缚。

为何三维如此艰难？

尽管二维问题已经被解决，但三维空间的复杂性远远超出了预期。三维空间中的方向和旋转路径呈现出更加复杂的交错与重叠模式，这使得传统的贝西科维奇“面积压缩”技巧在三维中失效。即使是著名数学家沃尔夫（Thomas Wolff）在1995年提出的下界（维度≥2.5）也未能为解决问题提供突破。因此，王虹与Zahl的证明，可以说是在非常复杂的数学框架下取得的重大发现。

挂谷猜想的数学宇宙

挂谷猜想不仅仅是一个几何问题，它与多个数学领域密切相关，且有着深远的影响：

• 调和分析：傅里叶变换的限制猜想（Restriction conjecture）就需要依赖于挂谷猜想的基础。
• 流体力学：纳维-斯托克斯方程的解的奇点分析与挂谷集的结构相关。
• 数论与密码学：有限域上的挂谷集已被证明与伪随机数生成模型密切相关。

这些交织的领域，进一步展示了挂谷猜想在现代数学中的核心地位，表明它不仅仅是几何测度论中的一个难题，也为其他学科提供了重要的启发和应用。

未竟之旅：高维战场

尽管三维挂谷猜想已经被解决，但四维及以上的高维空间仍然是未知领域。数学家们推测，在n维空间中，挂谷集的维度应为n，但现有工具尚难处理高维代数簇的复杂性。王虹与Zahl的证明框架为高维推广提供了可能的路径，但高维战场依旧充满挑战。

数学史启示

挂谷猜想的百年历程正如数学家哈代所言：“真正的数学问题，其美感不因时间褪色，反因挑战而愈发璀璨。”这不仅是对数学家辛勤付出的致敬，也是对数学领域不断追求未知、探索极限的诠释。从针的旋转到空间的本质，挂谷猜想连接了分形几何、调和分析、数论等多个数学分支。三维的突破是数学史上的里程碑，而四维及以上的挑战则依旧未解，等待着未来数学家们继续探索。挂谷猜想的解决，正如数学家所言：“最优雅的问题，往往藏于最朴素的起点。”