引言

强化学习作为机器学习的一个重要分支，近十年来在人工智能领域取得了令人瞩目的进展，尤其是在如AlphaGo这样的世界级挑战中，强化学习展现出了强大的决策能力。AlphaGo通过深度强化学习的方法成功击败世界围棋冠军李世石，标志着人工智能在复杂决策问题上的突破性进展。AlphaGo利用深度神经网络与蒙特卡洛树搜索相结合，在每一次棋局中进行模拟，通过强化学习不断调整策略，从而实现了令人震惊的棋局表现。科学家们通过对AlphaGo背后的强化学习算法的分析，揭示了强化学习在复杂决策问题中的应用潜力。

同样，游戏AI（例如星际争霸这款游戏）也大量采用强化学习方法来优化决策、增强智能体的自我学习能力。随着深度学习技术的迅猛发展，强化学习与深度学习的结合逐渐成为解决复杂任务的核心方法之一。而近几个月特别火的DeepSeek等项目更是结合了强化学习与深度学习，推动了AI在复杂任务中的应用。DeepSeek等项目展示了深度强化学习在实际应用中的巨大潜力。通过将深度神经网络引入强化学习，DeepSeek等AI系统能够在极其复杂的环境中进行有效的决策优化，尤其是在大规模数据处理和高维空间的任务中，强化学习结合深度学习的方式能够提供更加准确和高效的解决方案。

在这些前沿的技术背景下，赵世钰研究员的《强化学习的数学原理》为我们提供了一本详细、深入理解强化学习背后数学原理的优秀著作。

本书从强化学习的基础概念讲起，逐步深入到了状态值、贝尔曼方程、值迭代与策略迭代等重要算法的推导，以及蒙特卡洛方法和策略梯度方法的应用。每一章都通过清晰的内容结构图和详细的数学推导，帮助读者理解复杂的算法原理，特别是适合那些希望进一步掌握强化学习深层次内容的读者。而要阅读这本书，读者需要掌握高等代数、线性代数、概率论与数理统计方面的知识，在此基础上来理解这本书会觉得更加容易一些。

详细来看，强化学习作为机器学习的一个重要分支，它的核心思想源于“试错”与“奖励反馈”，即智能体通过与环境的交互不断调整策略，以获得更大的长期回报。这本书从强化学习的基本概念出发，逐步深入探讨了包括状态值、贝尔曼方程、值迭代与策略迭代、蒙特卡洛方法、策略梯度方法等多个重要的数学工具和理论。在书中，每一章都给出了清晰的结构图，帮助读者系统地理解这些复杂的数学原理。下面，我们将对本书的结构进行深入分析，以便更好地理解本书是如何在书中构建强化学习的知识体系的。

本书的最大亮点之一是其深入浅出的教学方式，结合了扎实的理论基础和大量的实践应用。在赵世钰研究员的讲解下，复杂的数学推导得以通俗易懂地呈现，使得即便是对强化学习没有太多背景的读者，也能逐步掌握其核心思想和算法实现。本书通过精心设计的每一章内容，循序渐进地引导读者从理论到实践，从简单的状态值函数到深奥的策略梯度方法，都能在明确的框架中清晰呈现，避免了复杂内容对读者理解的阻碍。每一章的开头都有明确的目标和概述，帮助读者迅速抓住本章的核心内容；而章节的结束又通过总结和思考题，进一步巩固和加深读者的理解。

1. 基本概念与强化学习框架

在第一章，本书详细介绍了强化学习的基本框架，包括智能体（Agent）、环境（Environment）、状态（State）、动作（Action）、奖励（Reward）等核心概念。强化学习的核心思想是智能体通过与环境的交互，依据奖励信号调整自己的行为策略，从而最大化长期回报。这一部分不仅仅是对强化学习理论的概述，更通过具体的数学推导和实例分析，展示了这些概念如何在实际问题中发挥作用，尤其是如何通过优化策略来应对不确定性与复杂性。

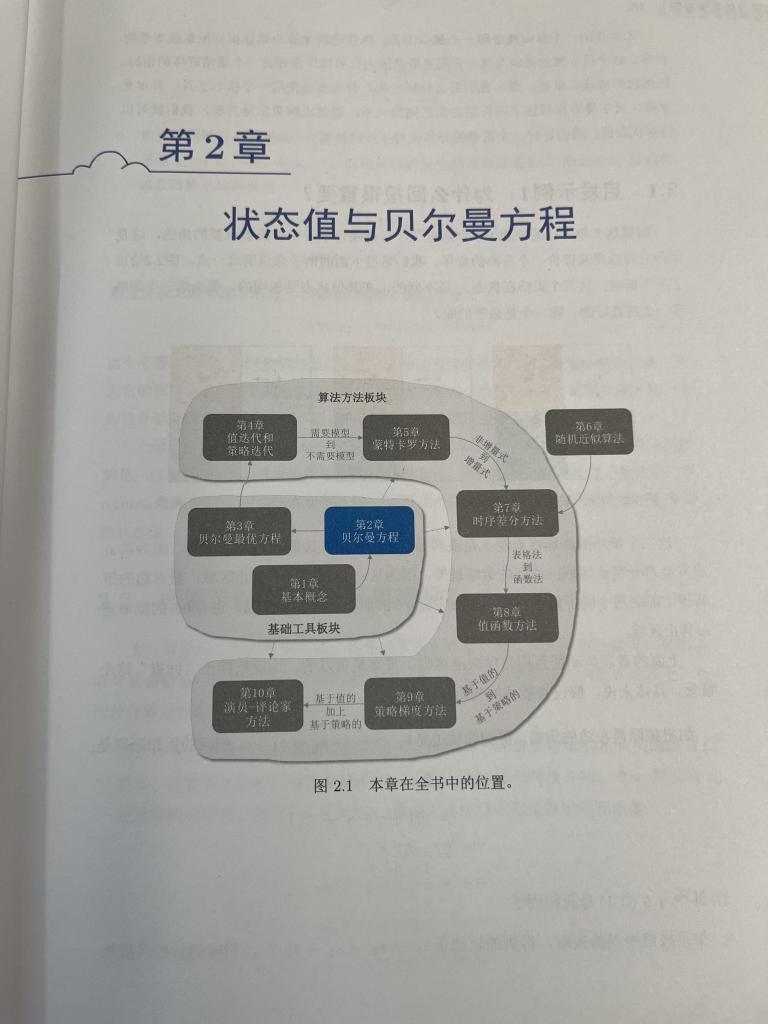
2. 状态值与贝尔曼方程

接下来，书中深入讲解了状态值函数的定义及其在强化学习中的作用。本书通过贝尔曼方程的形式来描述状态值与动作值之间的递归关系，为强化学习中的动态规划方法提供了数学基础。贝尔曼方程在强化学习中起到了至关重要的作用，它能够帮助我们从全局最优的角度将问题分解为子问题，从而简化求解过程。在这一部分，本书给出了详细的推导过程，帮助读者深入理解贝尔曼方程的本质及其实际应用。

3. 值迭代与策略迭代

在书的第三部分，本书讲解了值迭代与策略迭代两种经典的强化学习算法。值迭代通过反复迭代更新状态值函数，最终收敛到最优策略；而策略迭代则通过交替更新策略和状态值函数来逐步逼近最优解。本书清晰地展示了这两种方法的数学细节，并且用直观的图示和示例帮助读者理解这两种算法的工作原理。通过这一部分的学习，读者能够掌握如何通过动态规划方法求解强化学习中的最优策略。

4. 蒙特卡洛方法

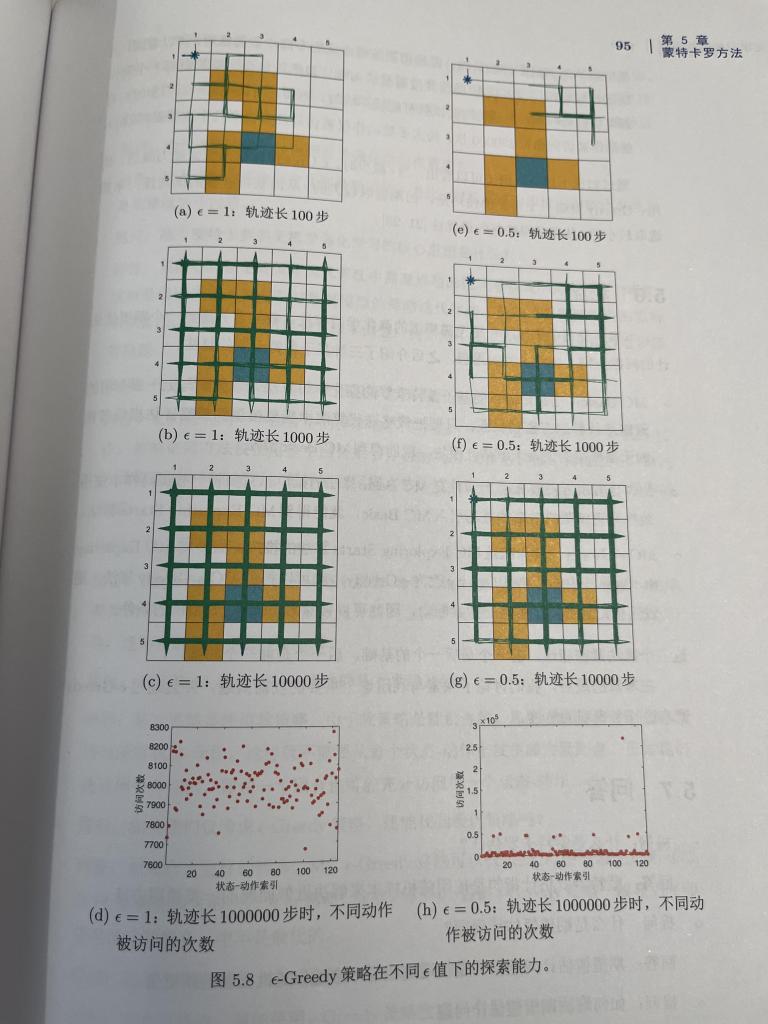
蒙特卡洛方法作为一种基于随机采样的强化学习算法，书中也给予了充分的讨论。本书详细介绍了蒙特卡洛方法如何通过模拟随机实验来估计状态值和动作值，并通过大量的经验数据来逼近最优策略。这种方法不依赖于环境模型，尤其适用于那些无法显式建模的复杂环境。通过图文并茂的描述，本书清晰地阐释了蒙特卡洛方法的基本原理及其应用，帮助读者在实践中有效利用这一方法。

5. 策略梯度方法

在书的最后，本书深入讲解了策略梯度方法，这是一种基于梯度上升的强化学习算法，用于直接优化策略的参数。策略梯度方法在深度强化学习中有着广泛应用，尤其是在高维度的复杂任务中，策略梯度方法可以避免传统值迭代方法在大规模状态空间中的计算瓶颈。本书通过清晰的推导与实例，帮助读者理解如何利用梯度上升算法优化强化学习模型，从而提高决策性能。

书籍结构与阅读体验

《强化学习的数学原理》全书结构清晰，内容层次分明，每一章都以理论推导为基础，并辅以丰富的图示，帮助读者逐步消化和理解抽象的数学概念。书中不仅对强化学习的基本原理进行了详细讲解，还涵盖了现代强化学习中的一些高级技术，如策略梯度方法和深度强化学习的结合。本书通过生动的案例分析，尤其是结合如AlphaGo、游戏AI等实际应用，帮助读者更好地理解这些数学原理在真实世界中的应用场景。

《强化学习的数学原理》是一本内容丰富、结构严谨的专业书籍，适合那些希望深入了解强化学习背后数学机制的读者。不仅适合作为大学生或研究生的教材，也非常适合工程师或研究人员用来作为提高自己强化学习理论水平的参考书。无论是从基础的状态值函数、贝尔曼方程到复杂的蒙特卡洛方法、策略梯度方法，本书都做了细致的讲解，确保读者能够掌握强化学习的核心概念和方法。另外，书中大量图示和实例的应用，也使得这些数学原理更加易于理解，尤其对于强化学习初学者来说，具有重要的启发意义。通过本书，读者不仅能掌握强化学习的基础理论，还能了解其在现代人工智能领域中的前沿应用，特别是如何通过强化学习与深度学习的结合，推动智能决策系统的发展。