探秘 2025：一个充满惊喜的数学之年

今年是 2025 年，这个看似普通的四位数字，其实隐藏着丰富的数学奥秘。从质因数分解来看，它是一个完全平方数，可以写成 $45^2 = 2025$ 。除此之外，2025 这个数字在数字分解，求和以及各种特殊的数列中展现了其迷人的规律。从质因数分解到数论研究，2025 不仅仅是一个年份，更是一扇通向数论研究的窗口。在这篇文章中，我们将一同揭开 2025 的神秘面纱，探索它背后那些令人惊叹的数学性质和规律。或许，作为读者的你会发现，这个年份远比你想象的更加有趣。

在数学中，若一个数是一个整数的平方，则称这个数是完全平方数，简称平方数。逐一写出那就是 $1,4,9,16,25,\cdots,n^2,\cdots$ ，这里的 $n$ 代表某个正整数。而 2025 恰好是一个完全平方数，直接计算可以得到 45 乘以 45 等于 2025。同时，比 2025 略小的完全平方数是 $44^2=1936$ ，比 2025 略大的完全平方数是 $46^2=2116$ 。也就是说，在近代能够在一生中经历两个完全平方数年份的人必定是高寿之人。

另外，对 2025 这个数字的每一位都加上 1，它就变成了 3136，它依然是完全平方数，换言之， $3136 = 56^2$ 。满足这个条件的自然数非常“稀疏”，通过计算可以得到：

$0, 25=5^2,2025=45^2,13225=115^2,\cdots$ ，

都满足每一位加上 1 之后依旧是完全平方数，因为

$1, 36=6^2, 3136=56^2, 24336=156^2,\cdots$ 。

在此基础上对 2025 进行质因数分解可以得到

$2025 = 45^2=(9\times 5)^2 = 3^4\times 5^2 = 1\times 3^4 \times 5^2$ ，

在这个式子中， $1,2,3,4,5$ 这五个数字有且仅被使用了一次，通过乘法和幂运算就得到了 2025 这个数字。

如果对等差数列求和计算熟悉的读者，一定知道这样一个著名的故事，那就是数学王子高斯小时候计算从 1 加到 100 的故事，最终的答案是 5050。而这个数学公式就是等差数列的求和公式：

$1+2+\cdots+n=\frac{n(n+1)}{2}$ 。

证明这个公式的关键就是首尾逐项相加之和相等。2025 恰好是 45 的平方，45 这个数字恰好又是从 1 加到 9 之和，换言之， $1+2+3+\cdots+9=45$ ，那么

$2025=45^2=(1+2+\cdots+9)^2$ 。

除了自然数的求和公式之外，数学家们还研究了自然数的平方和，立方和，甚至四次方和等公式。例如：

$1+2+\cdots+n=\frac{n(n+1)}{2}$ ，

$1^2+2^2+\cdots+n^2=\frac{n(n+1)(2n+1)}{6}$ ，

$1^3+2^3+\cdots+n^3=\big(\frac{n(n+1)}{2}\big)^2$ 。

因此， $(1+2+\cdots+n)^2=1^3+2^3+\cdots+n^3$ 。所以，2025 可以进一步地写成

$2025 = 1^3+2^3+\cdots+9^3$ 。

同时，2025 还可以表示为三个正整数的平方和：

$2025 = 40^2+20^2+5^2$ 。

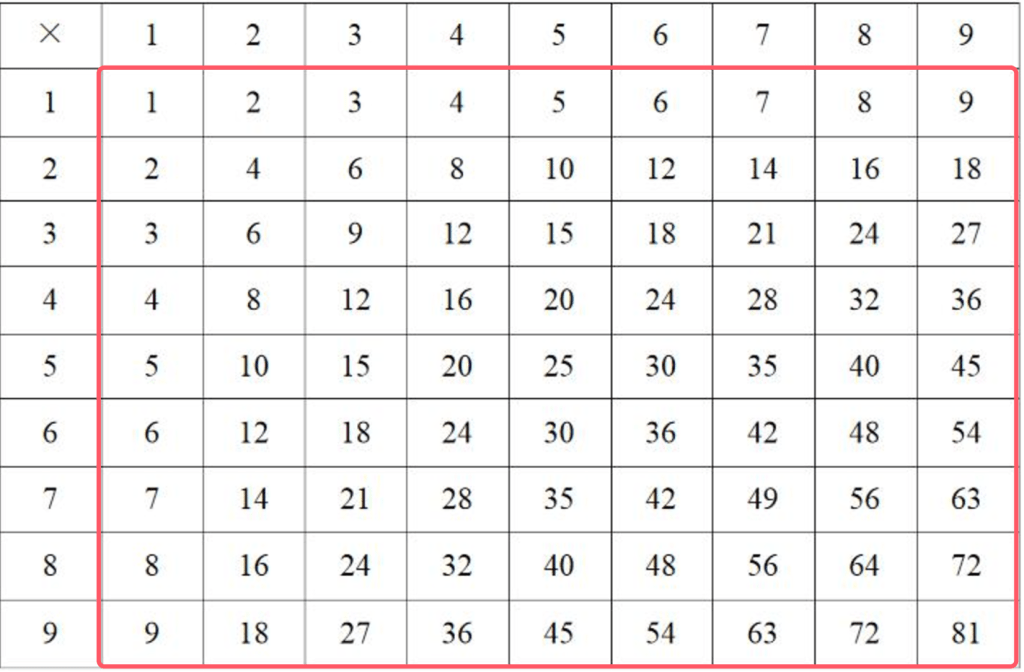
九九乘法表是大家都非常熟悉的表格，当我们把表格中红框的所有数字求和之后，我们会发现它的和恰好就是 2025。因为，

$\sum_{i=1}^{9}\sum_{j=1}^{9}i\times j = \sum_{i=1}^{9}i\times\sum_{j=1}^{9}j = 45\times 45 = 2025$ 。

哈沙德数（Harshad number）是可以在某个固定的进位制中，被各位数字之和（数字和）整除的整数。在十进制中，100以内的哈沙德数是：1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100。通过计算我们可以得到 2025 恰好也是哈沙德数，因为

$2025 = (2+0+2+5)\times 225$ 。

更巧的是，225 同样也是哈沙德数，因为 $225 = (2+2+5)\times 25$ 。所以说，2025 就是 2 重哈沙德数，换言之，

$2025 = (2+0+2+5)\times (2+2+5)\times 25$ 。

印度数学家卡普列加（Dattaraya Ramchandra Kaprekar, 1905 – 1986）在一次旅行中，遇到猛烈的暴风雨，他看到路边一块牌子被劈成了两半，一半上写着 30，另一半写着 25。这时，他忽然发现 $30+25=55$ ， $55^2=3025$ ，把劈成两半的数加起来，再平方，正好是原来的数字。从此他就专门搜集这类数字。按照第一个发现者的名字，这种怪数被命名为“卡布列克数”或“雷劈数”或“卡布列克怪数”。

雷劈数是自然数的一类，它的定义是如果正整数X（在n进位下）的平方可以分割为二个数字，而这二个数字相加后恰等于X，那么X的平方就是（n进位下的）一个雷劈数，又称卡布列克数。例如 $55^2=3025$ ，而 $30 + 25 = 55$ ，那么 3025 就是一个雷劈数。 $45^2=2025$ ，而 $45 = 20 + 25$ ，那么 2025 也是一个雷劈数。