《少儿几何启蒙》是一套富有创意与启发性的数学启蒙书籍,共包含四本,分别涵盖了立体图形和学会推理等内容。特别值得一提的是其中的两本——《立体图形》和《学会推理》,它们不仅在几何知识的呈现上非常精致,更通过生动的学生与老师对话,将抽象的数学理论与实际的思维训练相结合。
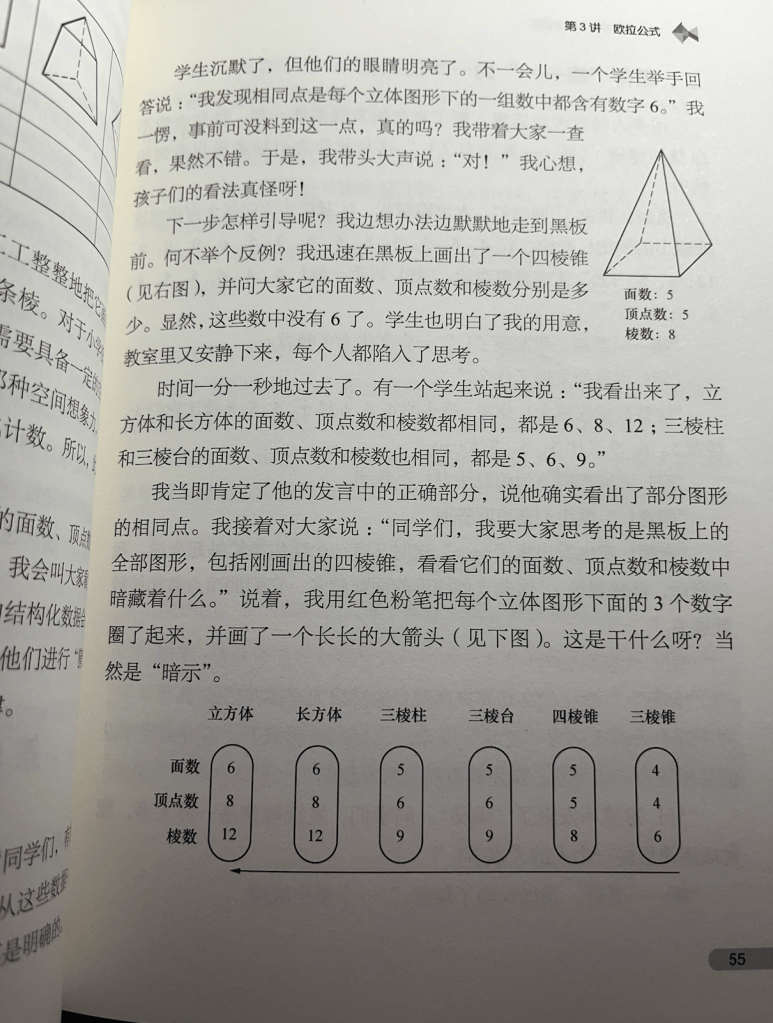
《立体图形》深入浅出地讲解了表面积与体积的概念,欧拉公式以及立体图形的切分等内容。通过丰富的图示和通俗易懂的语言,书中成功地将复杂的几何问题变得直观而易于理解。尤其是在讲解欧拉公式时,书中通过互动式的对话,使学生不仅能理解公式的表面,还能思考背后的逻辑和应用,这种“讲解+思考”方式,既避免了枯燥的死记硬背,又能激发学生的数学兴趣和探究欲望。
《立体图形》也像是数学教育家波利亚的《怎样解题》对于儿童的简化版,书中的对话情节通过学生与老师的互动,让孩子在解题过程中学会如何分析问题、推理和归纳。每一章内容都循序渐进,注重培养学生的数学思维能力,而不仅仅是传授知识。这种方式非常适合初学者,既能帮助他们建立数学框架,也能培养解决问题的能力。
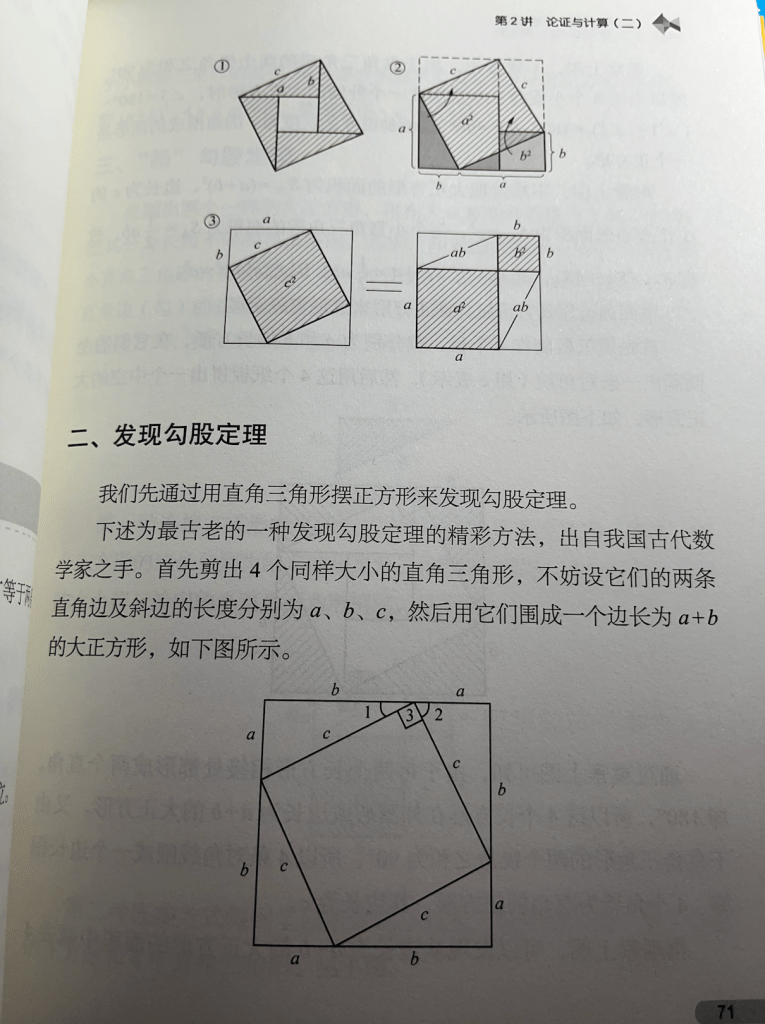
《学会推理》这本书则是用大量的定理和例子来向学生讲解了平面几何的诸多性质,包括勾股定理、三角函数等基础知识,让学生在阅读了这本书之后可以对平面几何有着跟进一步的了解和认识。
这套书的优点在于它以轻松、有趣的方式将数学的逻辑性与思维训练融入日常学习,帮助学生在探索几何世界的过程中,打下坚实的思维基础。对于家长和老师来说,这也是一本非常值得推荐的教学辅导书,让孩子在探索几何的同时,学会如何思考、如何解决问题。